机器调度(JSP)问题数学模型-EW帮帮网

JSP 问题（Job-Shop Scheduling Prob lem ）需要人员、物料、设备等多种资源优化整合，涉及到各类生产要素，具有数据量大、种类繁多的特点，同时加工任务也具备多品种、多批量、多工序、多任务等特征，是一个 NP-hard 问题。如何有效提高资源的利用率，缩短加工周期、合理规划工件各工序的加工流程一直是研究的热点。

关于JSP（机器调度问题），我们先考虑一个有3个待加工工件和4台加工机器的模型。每个工件都必须由相对应的机器按照给定的顺序进行处理，并且不存在循环加工。每个工件i在机器j上面的处理称为操作（k、i），其持续时间为 $t_{i}^{k}$ ，我们的目标是最小化最大完工时间。

条件假设工件1依次被机器1，2，3加工，工件2依次被机器2，1，4，3加工，工件3依次被机器1，2，4加工，因为工件的生产加工是要按照一定的流程进行，所以我们可以先绘制每一个工件的工作的图的模型。

从机器的角度来看，我们注意到，机器1，2分别需要加工工件1，2，3；机器3分别需要加工工件1，2；机器4分别需要加工工件2，3，所以存在机器先加工哪一个工件的可以使总的加工时间最少的问题。

观察到图中没有循环路径出现，我们考虑用图论来解决。构造一个虚拟始点和终点，得到下图。

我们开始建立机器调度的数学模型：

我们设（k，i）的加工完成时间为 $c_{i}^{k}$ ，

我们的目标是求最小化最大完工时间，只需要考虑每一个工件的最后一道工序的完工时间，因此建立目标函数：z= $min$ { $c_{1}^{3}$ , $c^{3}_{2}$ , $c_{3}^{4}$ }；

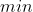
首先每一个工件的加工顺序是固定的（对应图中的实线部分），只有当前一台机器k完成对工件i的加工后，后一台机器h才能对工件i再进行加工，且工件的最开始加工时刻大于等于0，以第一个工件的加工为例，给出约束条件：

对于（1，1）： $c_{1}^{1}\geqslant t_{1}^{1}$

对于（2，1）： $c_{1}^{2}-t_{1}^{2}\geqslant c_{1}^{1}$

对于（3，1）: $c_{1}^{3}-t_{1}^{3}\geqslant c_{1}^{2}$

同理，工件2，3可以类似的建立相关的约束条件。

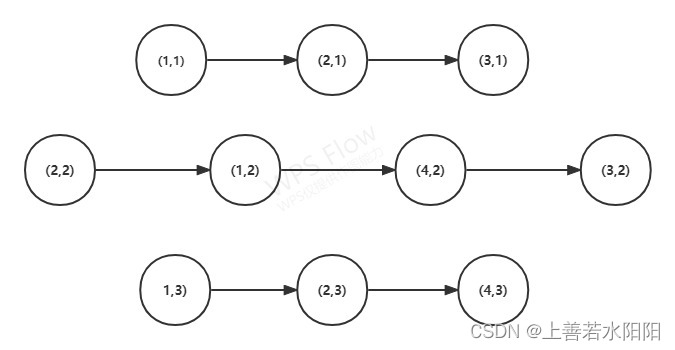
现在开始考虑同一台机器加工零件的先后顺序问题（对应图中虚线的部分）。每台机器对不同工件按照一定的顺序进行加工，要求每个工件只能加工一次，且每一台机器的必须在完成对某一个工件加工后，才能对该工件的紧邻后续工件进行加工。考虑图中（1，1），（1，2），（1，3）对应的部分，我们虚拟一个始点工件0，虚拟一个终点工件M。

设决策变量 $x_{ij}^{k}$ $\in \left \{ 0,1 \right \}$ ， $x_{ij}^{k}$ 表示机器k先加工工件i，完成对i的加工后，紧接着加工工件j，即机器加工工件j是机器加工工件i的紧后任务。

对于虚拟顶点0，有且只有一个紧后任务，在图中表示为有且只有一条指出的箭头，即： $x_{01}^{1}+x_{02}^{1}+x_{03}^{1}=1$

对于虚拟终点M，有且只有一个紧前任务，在图中表示为有且只有一条指向M的箭头，即：

$x_{1M}^{1}+x_{2M}^{1}+x_{3M}^{1}=1$

对于顶点（1，1），只有一个紧前任务和一个紧后任务，在图中表示为有且只有一条指出的箭头和一条被指向的箭头，即

$x_{01}^{1}+x_{21}^{1}+x_{31}^{1}=x_{12}^{1}+x_{13}^{1}+x_{1M}^{1}=1$

同理，对于（1，2）和（1，3）有：

$x_{02}^{1}+x_{12}^{1}+x_{32}^{1}=x_{21}^{1}+x_{23}^{1}+x_{2M}^{1}=1$

$x_{03}^{1}+x_{13}^{1}+x_{23}^{1}=x_{31}^{1}+x_{32}^{1}+x_{3M}^{1}=1$

现在考虑加工的时间约束，要求机器k完成对工件i的加工后，才能对紧邻的加工工件j进行加工。

$c_{1}^{1}\leqslant c_{2}^{1}-t_{2}^{1}+(1-x_{12}^{1})\times M$

$c_{2}^{1}\leqslant c_{1}^{1}-t_{1}^{1}+(1-x_{21}^{1})\times M$

$c_{1}^{1}\leqslant c_{3}^{1}-t_{3}^{1}+(1-x_{13}^{1})\times M$

$c_{3}^{1}\leqslant c_{1}^{1}-t_{1}^{1}+(1-x_{31}^{1})\times M$

$c_{2}^{1}\leqslant c_{3}^{1}-t_{3}^{1}+(1-x_{23}^{1})\times M$

$c_{3}^{1}\leqslant c_{2}^{1}-t_{2}^{1}+(1-x_{32}^{1})\times M$

对于顶点（2，1），（2，2），（2，3）和（3，1），（3，2）以及（4，2)，（4，3）可以做相同的处理。

由此，我们可以建立更一般的JSP问题的数学模型，将问题推广到更一般的情况。首先定义

1.下标（Index）：

工件：i

机器：j

工序：k

顶点：u

弧：e

2.集合（set）：

工件集合：I， $i\in I$

机器集合：J， $j\in J$

工序集合： $K_{i}$

顶点集合：V

弧集合：E

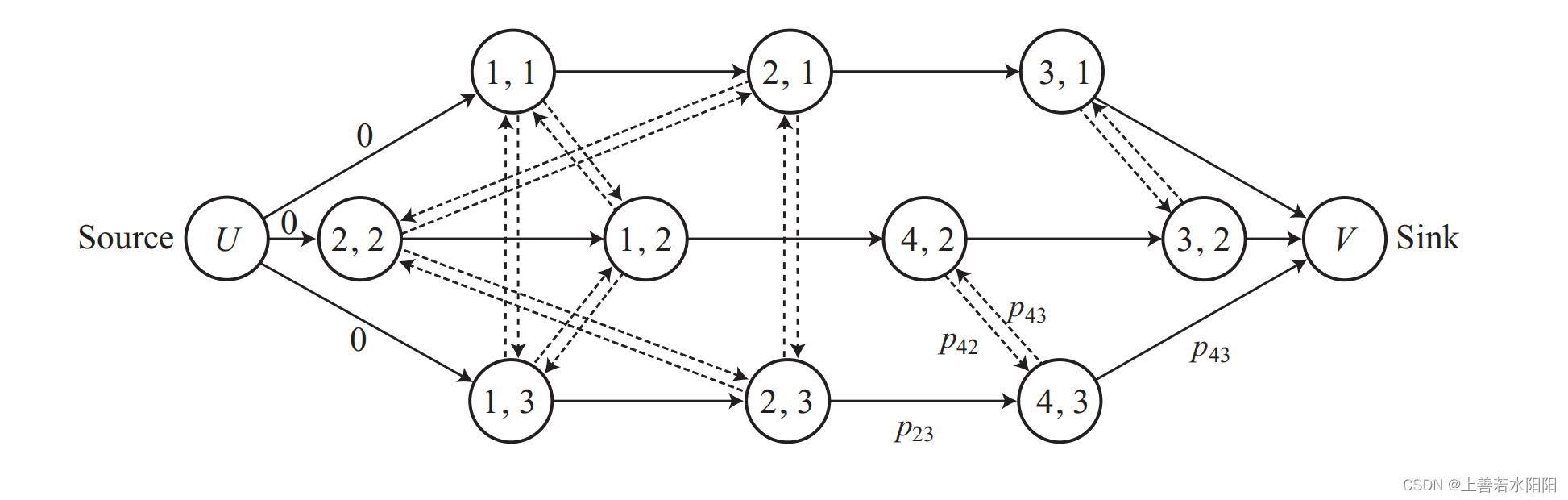
工件i对应的实线弧集合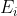： $E_{i}$

机器j对于的虚线弧集合： $A_{j}$

$A_{u}^{+}$ 表示流入u的虚线弧集合， $A_{u}^{-}$ 表示流出u的虚线弧集合

3.参数（paramet）：

加工时间： $t_{u}$

4.变量（variable）：

$c_{u}$ ：表示顶点u的完工时间，

$x_{e}$ ：表示弧e是否被选择，如果弧e被选择取1，否则取0

5.目标函数（Objective）：

min $max _{u\in V}$ { $c_{u}$ }

目标函数是最小化最大完成时刻。

6.约束条件（Constraints）：

$c_{u}\geqslant t_{u},u\in V$ (1)

$c_{u}\leqslant c_{v}-t_{v},u=t_{e},v=h_{e}, e\in E_{i},i\in I$ (2)

$\sum_{e\in A_{u}^{-}}^{} x_{e}=1,u=u_{j}^{0},j\in J$ (3)

$\sum_{e\in A_{u}^{+}}^{} x_{e}=1,u=u_{j}^{1},j\in J$ (4)

$\sum_{e\in A_{u}^{-}}^{} x_{e}=\sum_{e\in A_{u}^{+}}^{} x_{e}=1,u\in V_{j}\setminus\left \{ u_{j}^{0},u_{j}^{1} \right \}$ (5)

$c_{u}\leqslant c_{v}-t_{v}+(1-x_{e})M,u= t_{e}, v=h_{e},e\in A$ (6)

$x_{e}=0\ or \ 1$ (7)

约束条件（1）表示所有加工任务的完工时刻必须大于等于零时刻加上工件被机器加工的执行时间；约束条件（2）表示对于每一个工件，必须按照要求的顺序进行加工，紧后工序的完成时刻减去加工时间要大于等于紧前任务的完工时刻；约束条件（3）表示每一台机器最开始只能对一个工件进行加工；约束条件（4）表示每一台机器最后只能对一个工件进行加工；约束条件（5）表示除头尾两个机器加工任务外，每一个工件被机器加工有且只有一个紧前任务和紧后任务；约束条件（6）表示对于同一台机器，紧后任务的完工时刻减去执行时间大于等于紧前任务的完工时刻；约束条件（7）表示每一条路径只能取0和1两种类型。

机器调度(JSP)问题数学模型

网站公告

今日签到

热门文章

最新发布