2023.8.24

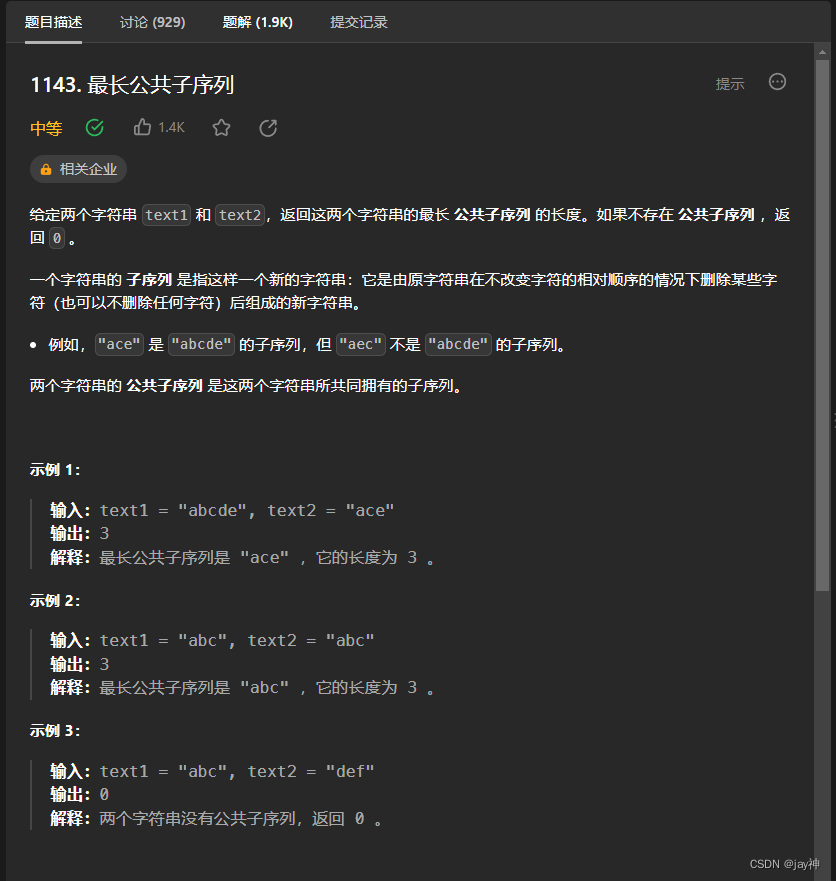
        本题是求公共子序列，即不连续。 定义一个二维dp数组，dp[i][j]含义：结尾下标为i-1的text1字符串和结尾下标为j-1的text2字符串之间的最长公共子序列。 这里二维数组的大小定义为[text1.size()+1,text2.size()+1],是为了省去初始化的操作，这题最长重复子数组则是有初始化的操作。 接下来就是两层for循环遍历两个字符串，无非就两种情况，当字符相同时，dp[i][j] = dp[i-1][j-1] + 1;  字符不同时：dp[i][j] = max(dp[i-1][j] , dp[i][j-1]);

        下面上代码：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size()+1,vector<int>(text2.size()+1,0));
        for(int i=1; i<=text1.size(); i++)
        {
            for(int j=1; j<=text2.size(); j++)
            {
                if(text1[i-1] == text2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[text1.size()][text2.size()];
    }
};