矩阵求导的本质与分子布局、分母布局的本质（矩阵求导——本质篇）
说在前面
我将严谨地说明矩阵求导的本质与分子布局、分母布局的本质。希望对初学的同学、想理解本质的同学提供一些帮助。
注1:看懂本文只需了解本科阶段高等数学的偏导如何求、本科阶段线性代数的矩阵的定义，无需任何其他知识。
注2：本文若无特殊说明，则约定向量均为列向量，如
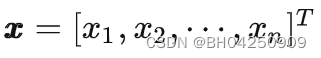
注3：本文仅考虑实数，不考虑复数。
一. 函数与标量、向量、矩阵
考虑一个函数
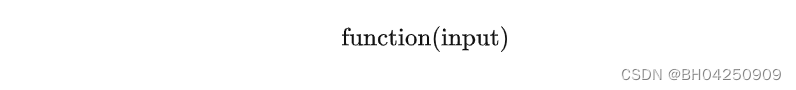
针对 function 的类型、input 的类型，我们可以将这个函数funcion分为不同的种类。
1、function是一个标量
我们称function是一个实值标量函数。用细体小写字母f表示。
1.1 input是一个标量
我们称function的变元是标量。用细体小写字母x表示。
例1：
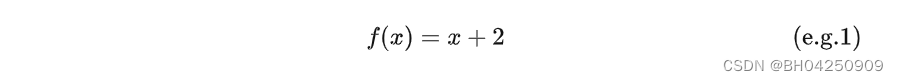
1.2 input是一个向量
我们称function的变元是向量。用粗体小写字母x表示。
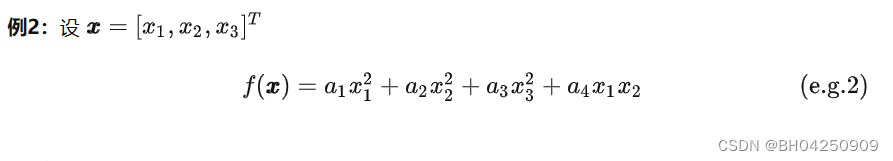1.3 input是一个矩阵
我们称function的变元是矩阵。用粗体大写字母X表示。
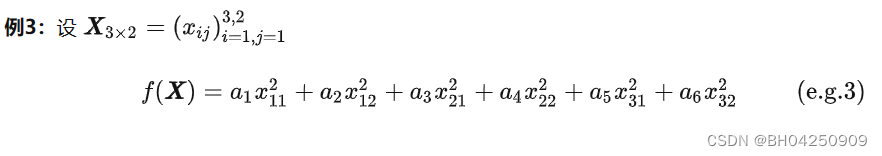
2、function是一个向量
我们称function是一个实向量函数。用粗体小写字母f表示。
含义:f是由若干个f组成的一个向量。
同样地，变元分三种:标量、向量、矩阵。这里的符号仍与上面相同。
2.1 标量变元
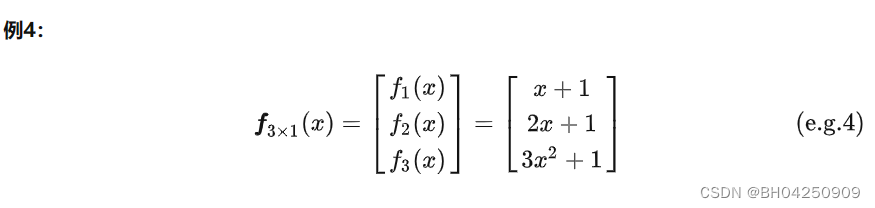
2.2 向量变元
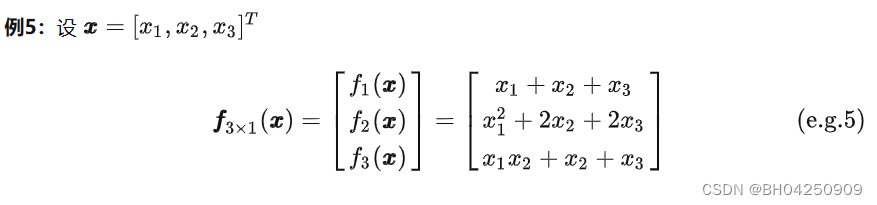
2.3 矩阵变元
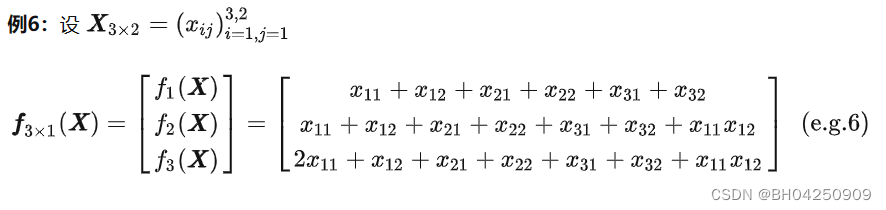
3、function是一个矩阵
我们称function是一个实矩阵函数。用粗体大写字母F表示。
含义:F是由若干个f 组成的一个矩阵。
同样地，变元分三种:标量、向量、矩阵。这里的符号仍与上面相同。
3.1 标量变元
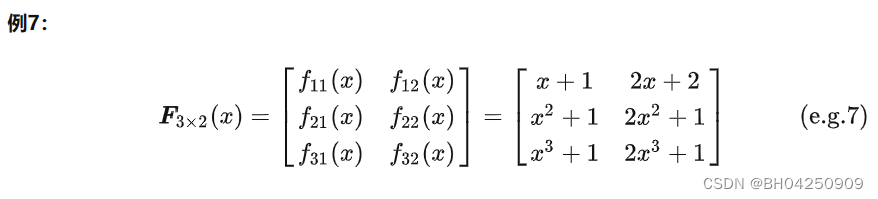
3.2 向量变元
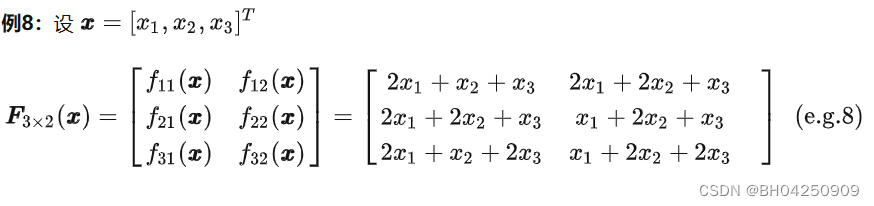
3.3 矩阵变元
4、总结
函数与标量、向量、矩阵
| function\input | 标量变元 | 向量变元 | 矩阵变元 |
|---|---|---|---|
| 实值标量函数 | f(x) | f(x) | f(X) |
| 实向量函数 | f(x) | f(x) | f(X) |
| 实矩阵函数 | F(x) | F(x) | F(X) |
二. 矩阵求导的本质
我们在高等数学中学过，对于—个多元函数：
至于这m × n个结果的布局，是写成行向量，还是写成列向量，还是写成矩阵，就是我们接下来要讨论的事情。
三. 矩阵求导结果的布局
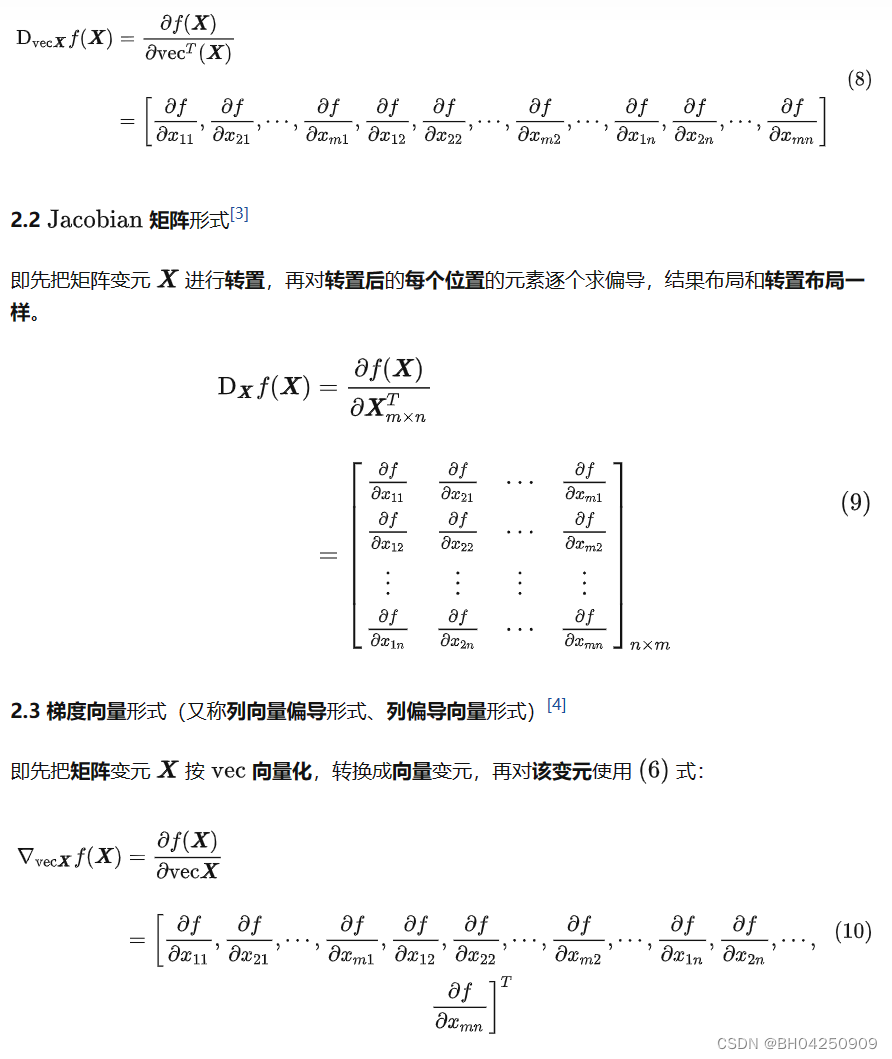
四. 分子布局、分母布局的本质
五. 向量变元的实值标量函数
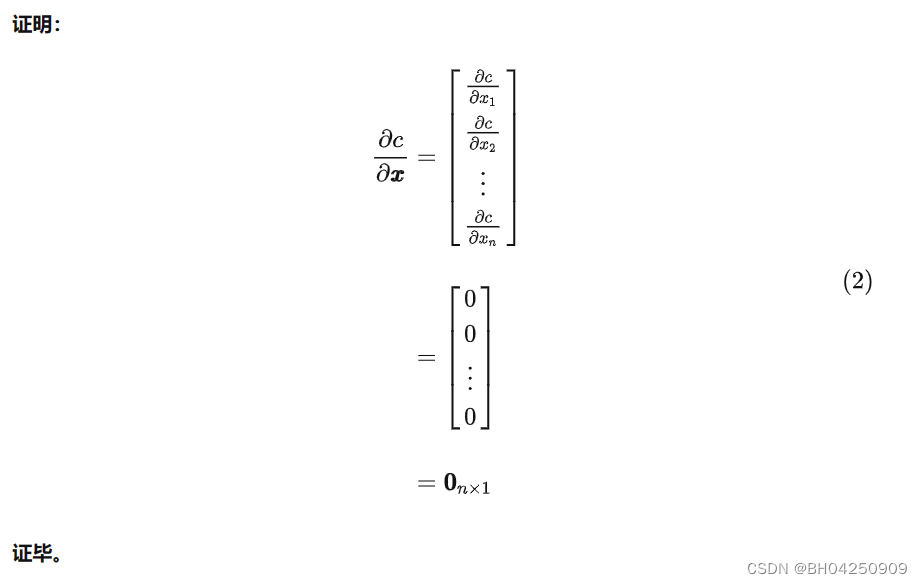
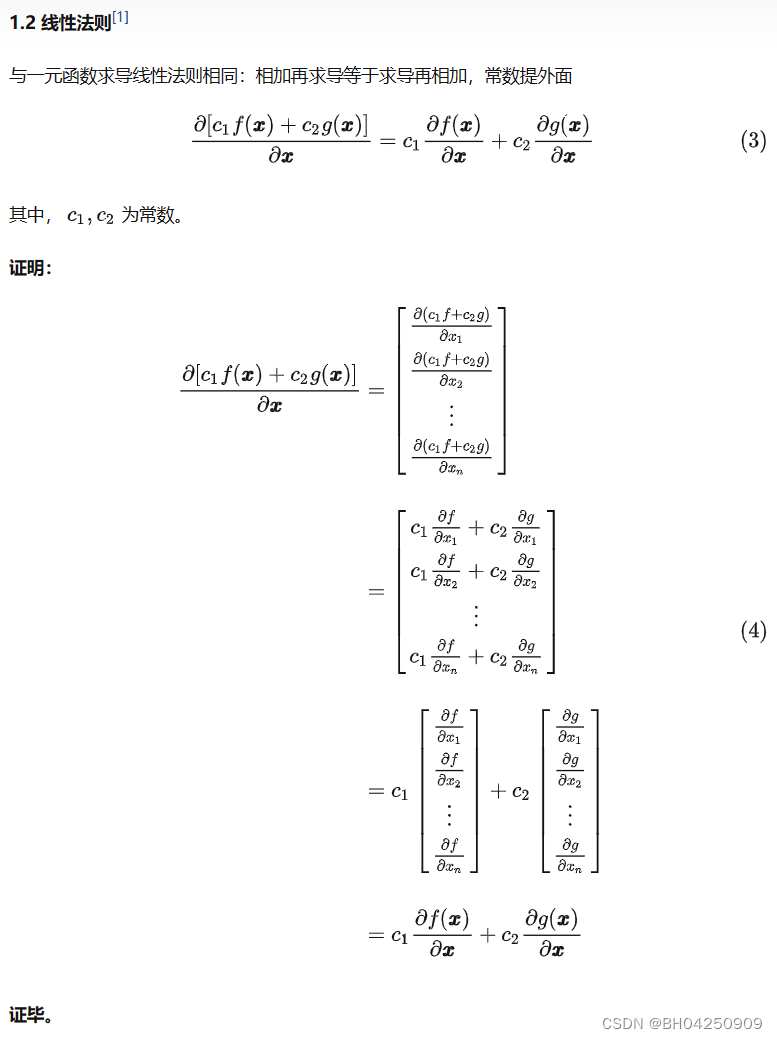
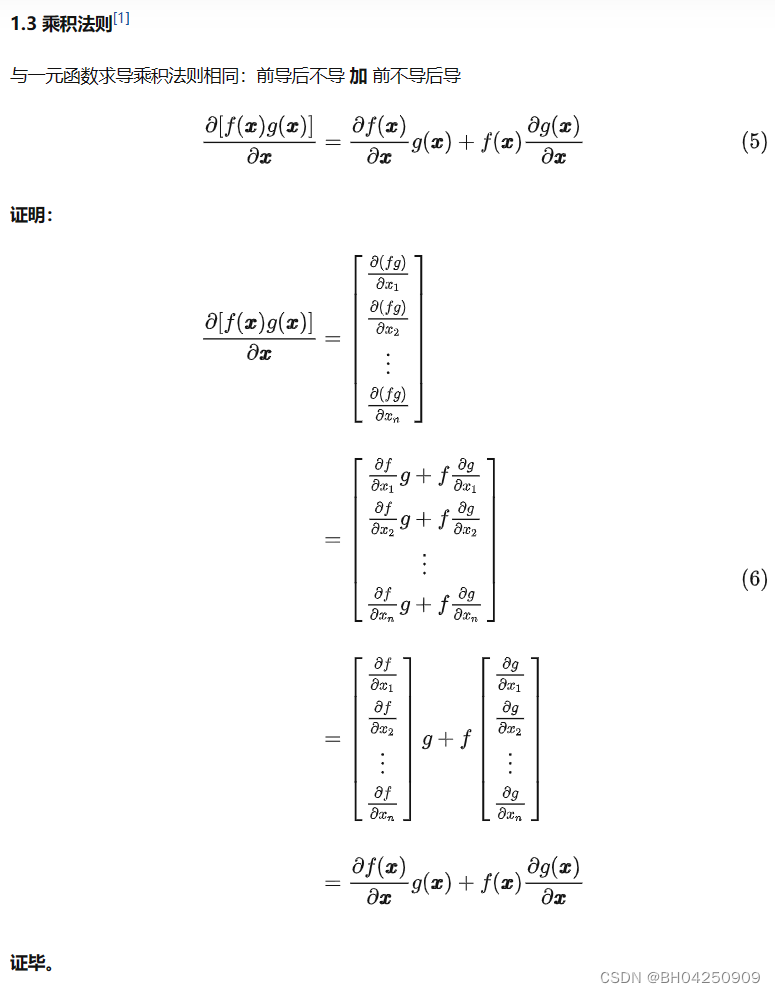
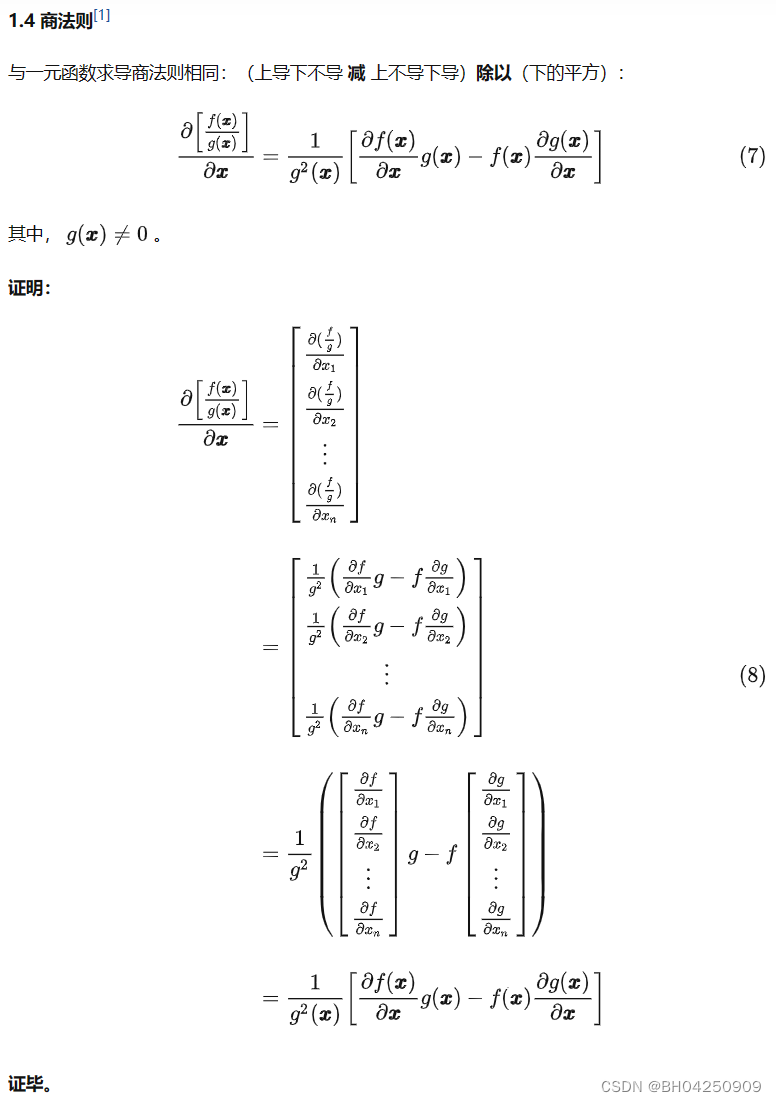
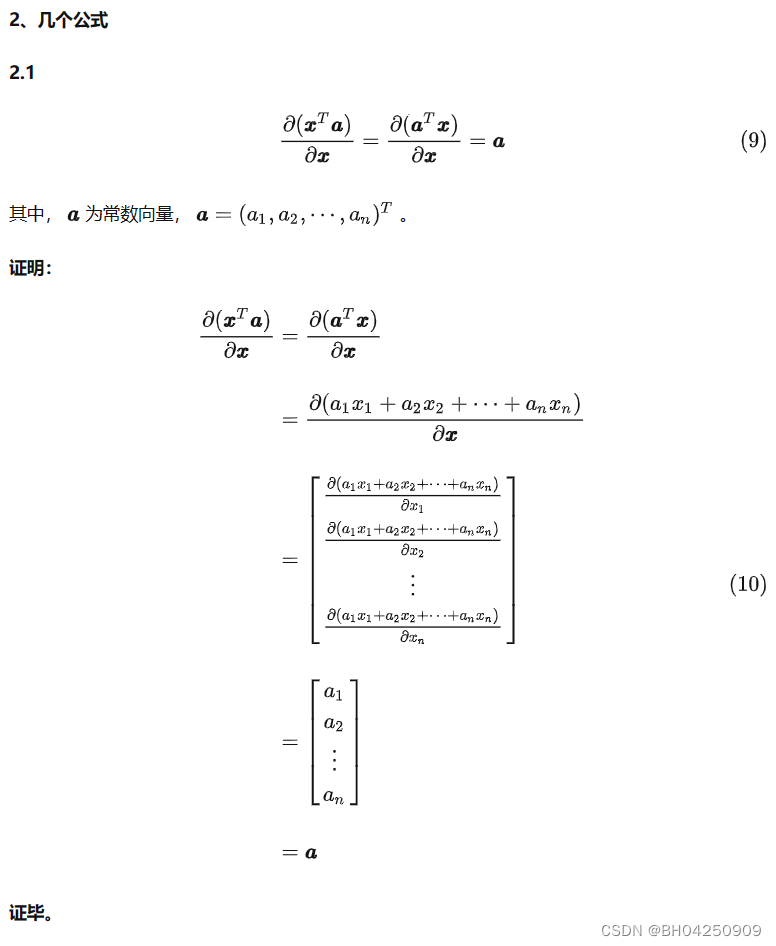
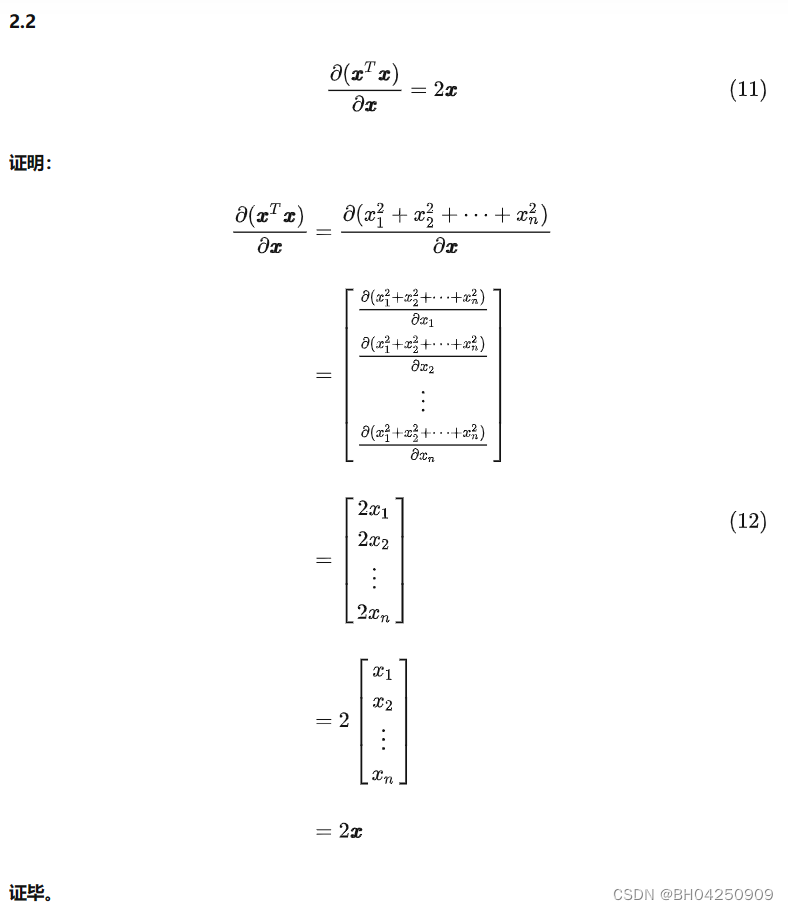
证毕。
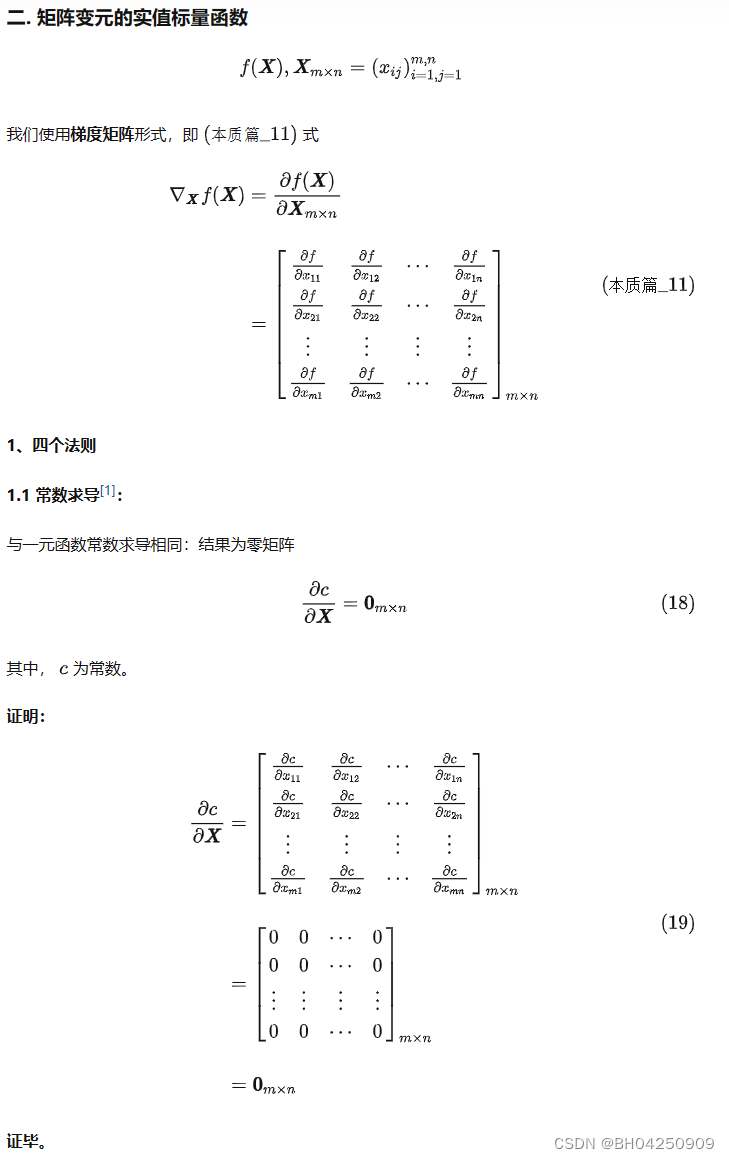
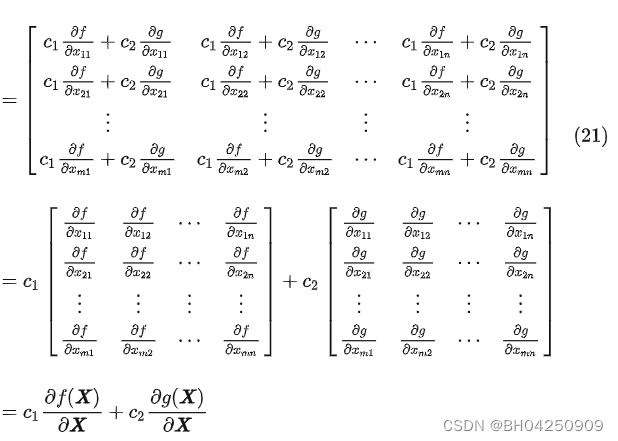
证毕。
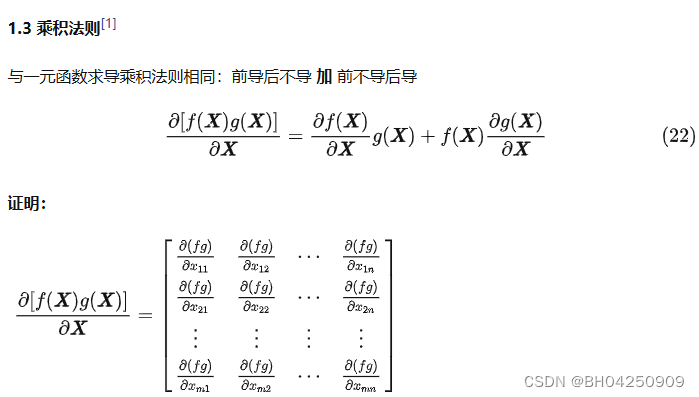
证毕。
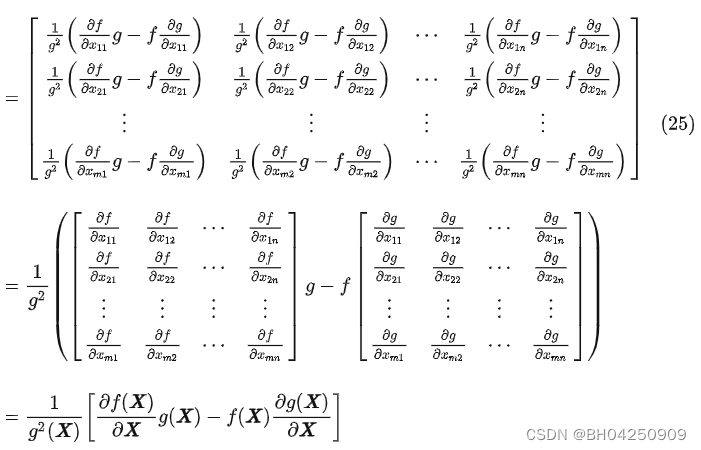
证毕。
