动态规划专题（笔记）

LeetCode 64. 最小路径和
打了一天游戏，没时间学习，要努力辽。
今天只是刷了一题leetcode，暂时以动态规划相关题型为复习点，编点工程代码。
新建./include/Solution.h

#include <vector>
using namespace std;
class Solution {
public:
    int minPathSum(vector<vector<int>> &grid);
};

新建./source/Solution.cpp

#include <vector>
#include <algorithm>
#include "Solution.h"
using namespace std;

int Solution::minPathSum(vector<vector<int>> &grid) {
    int rows = grid.size();
    int cols = grid[0].size();

    auto dp = vector<vector<int>> (rows, vector<int> (cols));
    dp[0][0] = grid[0][0];

    for(int i = 1; i < rows; i++) {
        dp[i][0] = dp[i-1][0] + grid[i][0];
    }
    for(int i = 1; i < cols; i++) {
        dp[0][i] = dp[0][i-1] + grid[0][i];
    }
    for(int i = 1; i < rows; i++) {
        for(int j = 1; j < cols; j++) {
            dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
        }
    }
    return dp[rows - 1][cols - 1];
}

新建./main.cpp

#include <vector>
#include <iostream>
#include "Solution.h"
using namespace std;

int main(int argc, char **argv) {
    int n,m;
    cin >> n >> m;
    auto grid = vector<vector<int>> (n, vector<int> (m));
    for (auto i = 0; i < n; i++) {
        for (auto j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    Solution mySolution;
    cout << mySolution.minPathSum(grid) <<endl;
    return 0;
}

新建./CMakeLists.txt

#声明要求的cmake最低版本
cmake_minimum_required(VERSION 3.0)

#声明一个cmake工程
project(Solution)

include_directories(include)

#添加一个可执行程序
#语法：add_executable(程序名 源代码文件)
add_executable(main_cmake main.cpp source/Solution.cpp)

执行

mkdir build
cd build
cmake ..
make
./main_cmake

测试用例

3
3
1 3 1 1 5 1 4 2 1

测试结果

7

LeetCode 72. 编辑距离
今天又是做帕鲁的一天，强撑着学点。

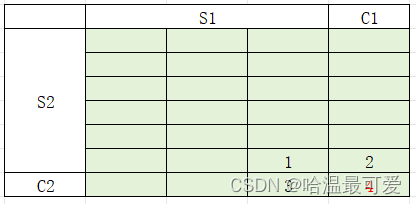
从字符串 S1 经过增/删/替换 转换到 S2 与
从字符串 S2 经过删/增/替换 转换到 S1 互为逆过程
上图中
1号单元记入字符串 S2 和字符串 S1 互转需要的最小步数
2号单元记入字符串 S2 和字符串( S1 + C1 )互转需要的最小步数
3号单元记入字符串( S2 + C2 )和字符串 S1 互转需要的最小步数
那么
4号单元可由1、2、3号单元内容计算得出。

class Solution {
public:
    int minDistance(string word1, string word2) {
        int s1 = word1.size();
        int s2 = word2.size();
        auto dp = vector<vector<int>>(s1 + 1, vector<int>(s2 + 1));
        for (int i = 1; i <= s2; i++) {
            dp[0][i] = i;
        }
        for (int i = 1; i <= s1; i++) {
            dp[i][0] = i;
        }
        for (int i = 1; i <= s1; i++) {
            for (int j = 1; j <= s2; j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
                }
            }
        }
        return dp[s1][s2];
    }
};