二分查找算法(1)

算法介绍

二分查找适用范围不止是有序数组，很多有“二段性”的数组其实都可以使用二分查找，什么是“二段性”呢？在数组中，我们查到某个数不符合条件后，就可以排除它之前或之后的所有数据，这种性质就叫做“二段性”！

我们的二分查找有三种情况：1.朴素的二分模板 2.查找左边界的二分模板 3.查找右边界的二分模板
这几种我们都会讲到！

704.二分查找

一、题目描述

OJ题目链接：力扣（LeetCode）

二、思路解析

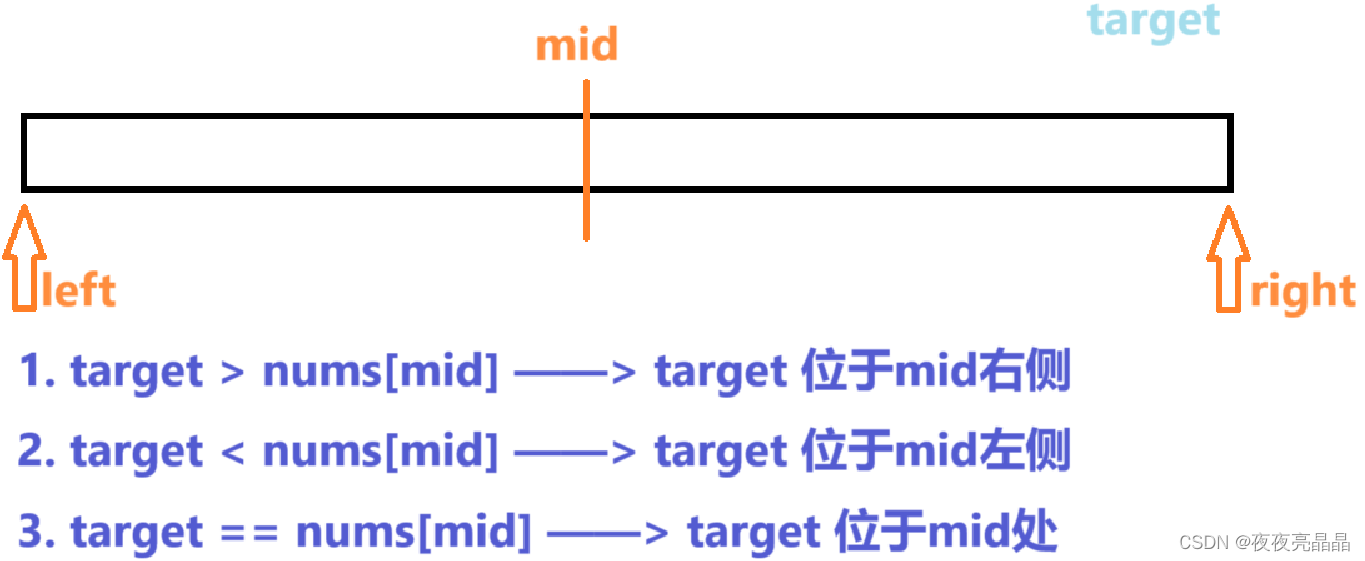
三、代码

class Solution {
public:
    int search(vector<int>& nums, int target) 
    {
        int left = 0, right = nums.size() - 1;
        while(left <= right)
        {
            int mid = (right - left) + left;
            if(nums[mid] == target) return mid;
            else if(target > nums[mid]) left = mid + 1;
            else right = mid - 1; 
        }
        return -1;
    }
};

34.在排序数组中查找元素的第一个和最后一个位置

一、题目描述

非递减顺序：两个相邻的数后面的大或者两数相等

时间复杂度O(logn)联想到二分查找！

二、思路解析

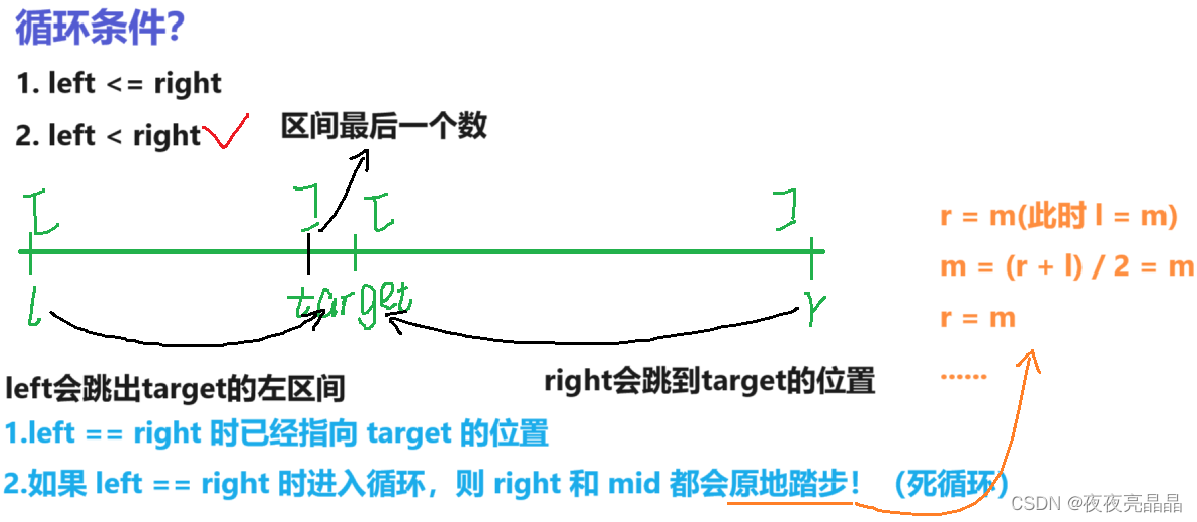
三、代码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        if(!nums.size()) return {-1, -1};//处理边界情况
        int left = 0, right = nums.size() - 1;
        int begin = -1, end = -1;
        while (left < right)
        {
            int mid = left + (right - left) / 2;
            if (nums[mid] >= target) right = mid;
            else left = mid + 1;
        }
        //判断是否满足题意
        if(nums[left] == target) begin = left;
        left = 0, right = nums.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if (nums[mid] > target) right = mid - 1;
            else left = mid;
        }
        if(nums[right] == target) end = right;
        return {begin, end};
    }
};

35.搜索插入位置

一、题目描述

OJ题目链接：力扣（LeetCode）

二、思路解析

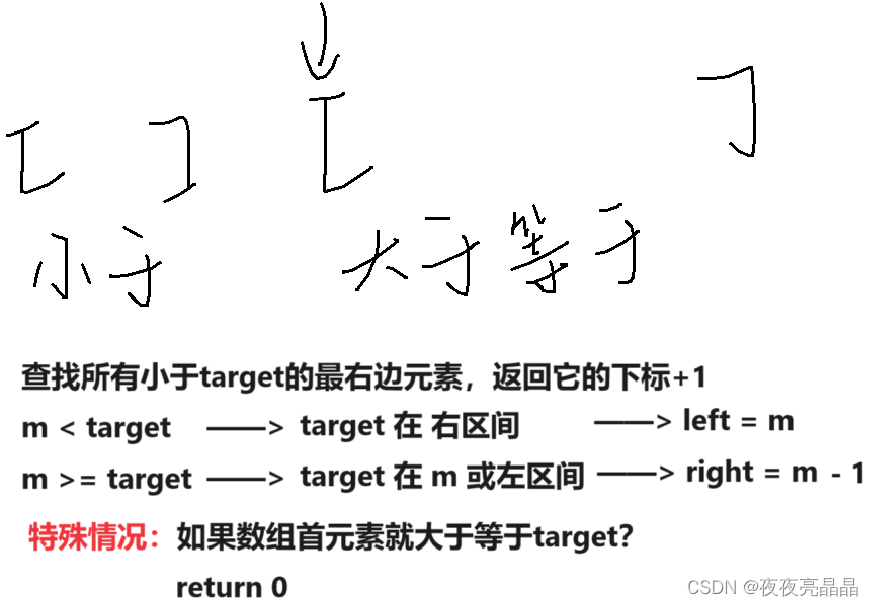
三、代码

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) 
    {
        int left = 0, right = nums.size() - 1;
        while (left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if(nums[mid] < target) left = mid;
            else right = mid - 1;
        }
    if (nums[left] >= target) return left;
    return left + 1;
    }
};

69.x的平方根

一、题目描述

OJ题目链接：力扣（LeetCode）

二、思路解析

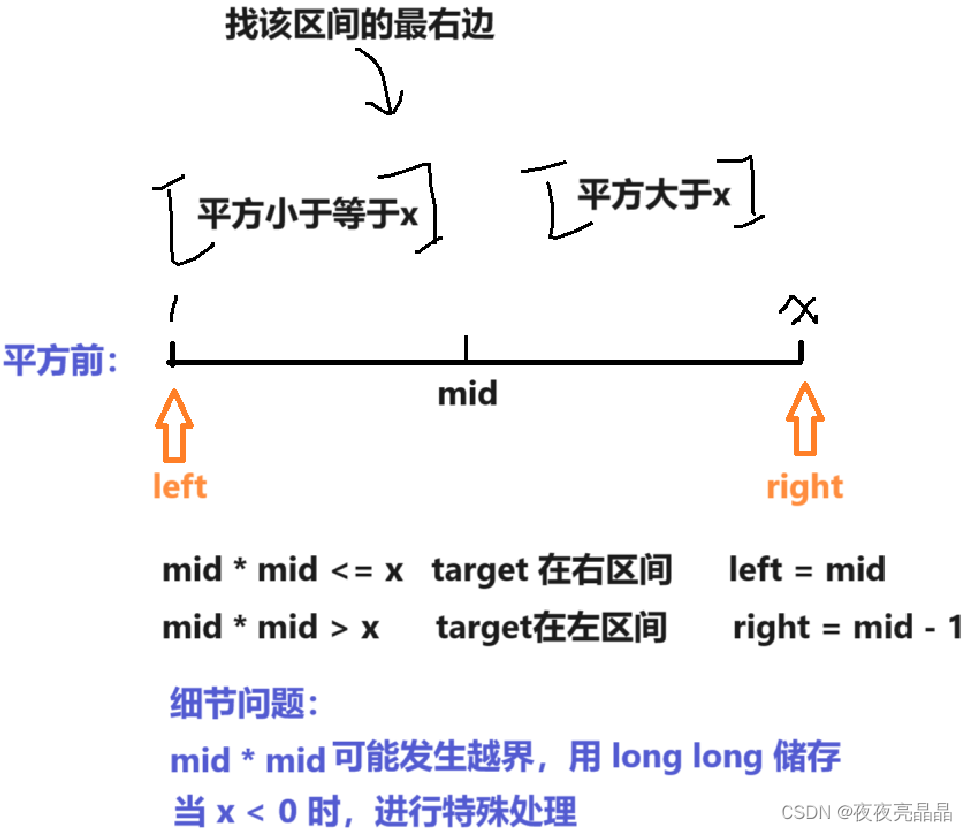
三、代码

class Solution {
public:
    int mySqrt(int x) 
    {
        if (x < 1) return 0;
        int left = 1, right = x;
        while (left < right)
        {
            long long mid = (long long)(left + (right - left + 1) / 2);
            if (mid * mid <= x) left = mid;
            else right = mid - 1; 
        }
        return left;
    }
};