LeetCode-78. 子集【位运算 数组 回溯】

题目描述：

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的
子集
（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

解题思路一：回溯，回溯三部曲

如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

其实子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和 子集{2,1}是一样的。

那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始！

有同学问了，什么时候for可以从0开始呢？

求排列问题的时候，就要从0开始，因为集合是有序的，{1, 2} 和{2, 1}是两个集合，排列问题我们后续的文章就会讲到的。

以示例中nums = [1,2,3]为例把求子集抽象为树型结构，如下：

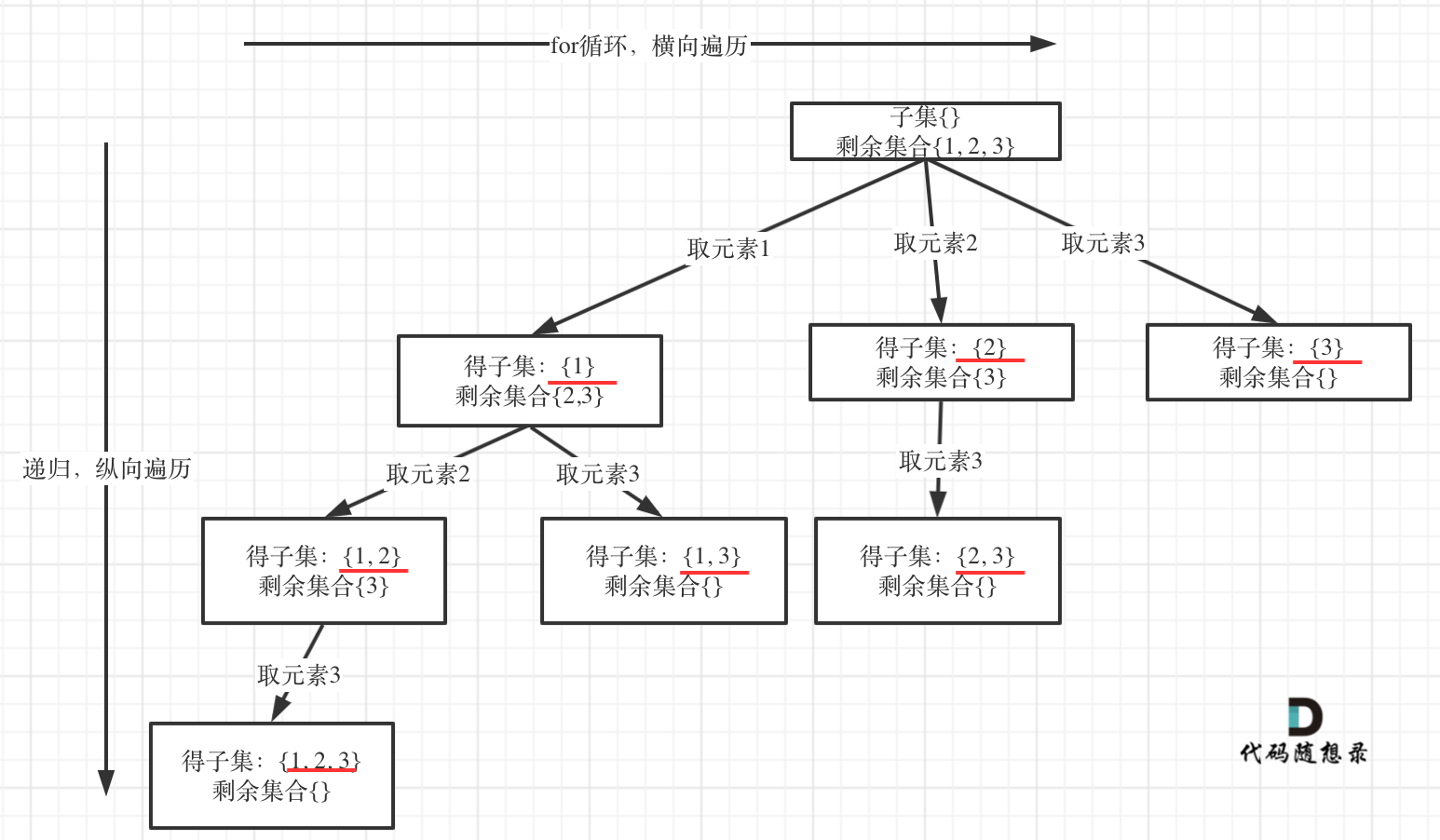
1. 递归函数参数

全局变量数组path为子集收集元素，二维数组result存放子集组合。（也可以放到递归函数参数里）

递归函数参数在上面讲到了，需要startIndex。

2. 递归终止条件

从图中可以看出：

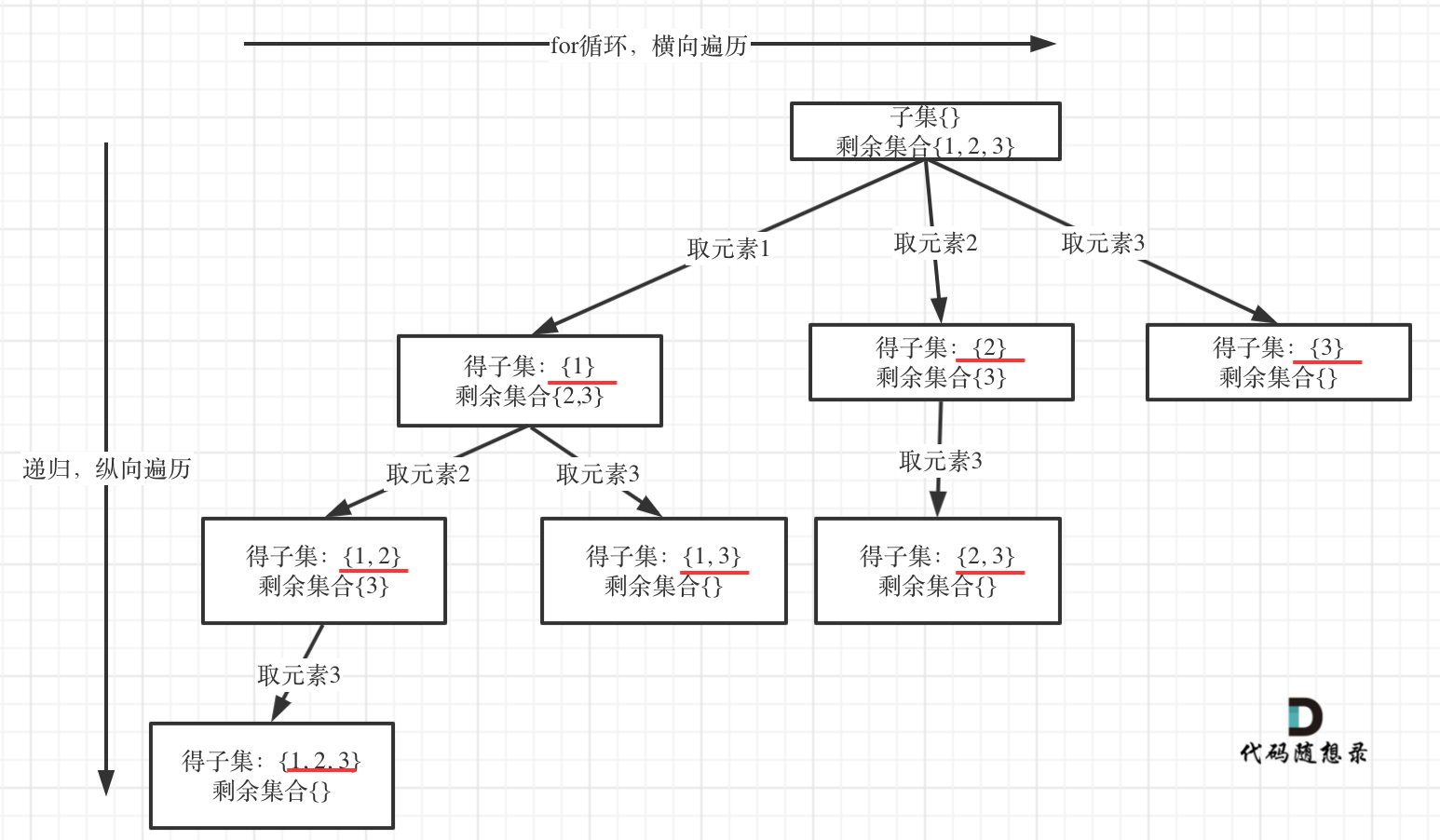
剩余集合为空的时候，就是叶子节点。

那么什么时候剩余集合为空呢？

就是startIndex已经大于数组的长度了，就终止了，因为没有元素可取了，其实可以不需要加终止条件，因为startIndex >= nums.size()，本层for循环本来也结束了。

3. 单层搜索逻辑
   求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        self.backtracking(nums, 0, [], res)
        return res
    
    def backtracking(self, nums, startIndex, path, res):
        res.append(path[:])
        for i in range(startIndex, len(nums)):
            path.append(nums[i])
            self.backtracking(nums, i + 1, path, res)
            path.pop()

时间复杂度：O(n * 2ⁿ)
空间复杂度：O(n)

解题思路二：0

时间复杂度：O(n)
空间复杂度：O(n)

解题思路三：0

时间复杂度：O(n)
空间复杂度：O(n)