动态规划概念：
给定一个问题，将其拆成一个个子问题，直到子问题可以直接解决。然后把子问题的答案保存起来，以减少重复计算。再根据子问题的答案反推，得出原问题解。
821
运行时间长的原因：
重复大量计算
以5个台阶为例：
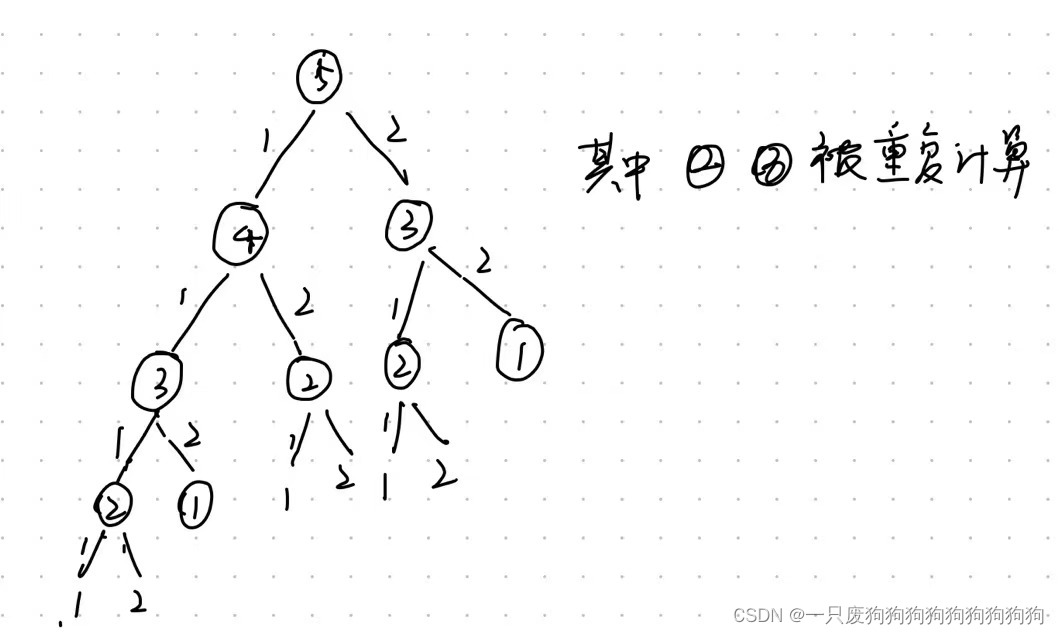正确做法：记录台阶已有的方案，比如用mem[]数组记录
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=30;
int n;
string words[N];//存单词
int used[N];//记录每个单词的使用次数
int g[N][N];//f[i][j] 存第i个单词能否接到第j个单词后面,存储相同子串长度
int res=0;
int mem[N];
int dfs(int x)//x代表遍历到的单词
{
if(mem[x])return mem[x];//如果以计算好直接返回
int sum=0;
if(x==1)
sum=1;
else if(x==2)//用else if
sum=2;
else sum=dfs(x-1)+dfs(x-2);
mem[x]=sum;//没有计算好则需要更新
return sum;
}
int main()
{
scanf("%d",&n);
int res=dfs(n);
printf("%d\n",res);
return 0;
}递推算法dp：
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=30;
int n;
int res=0;
int mem[N];
int main()
{
scanf("%d",&n);
mem[1]=1;
mem[2]=2;
if(n==1||n==2)
printf("%d",mem[n]);
for(int i=3;i<=n;i++)
{
mem[i]=mem[i-1]+mem[i-2];
}
printf("%d\n",mem[n]);
return 0;
}
进一步优化空间：
int newf=0,tmp1=1,tmp=2;
for(int i=3;i<=n;i++)
{
newf=tmp1+tmp2;
tmp1=tmp2;
tmp2=newf;}
记忆化搜索=暴力dfs+记录答案
递推的公式=dfs向下递归的公式
递推数组的初始值=递归的边界
acw1049
暴力搜索，分析图：
思路：最后一家店x只有两个可能，被选或者不被选，因为要尽可能的累加数值，所以被选的情况是一直累加到x-2,不被选的情况是只累加到x-1便结束
用home[N]数组保存已经选择的店家。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=30;
int n,k;
int res=0;
int mem[N];
int dfs(int x)//当前遍历到哪个店家
{
if(x>n)return 0;//dfs(5),dfs(6)都等于0，最终是可以组合的n个数字相加取最大值
else
return max(dfs(x+1),dfs(x+2)+mem[x]);//没被选择则是下一个数字，被选中则是隔一个数字
}
int main()
{
scanf("%d",&k);
while(k--)//循环输入k组数据
{
scanf("%d",&n);
for(int i=1;i<=n;i++)//位置是从1开始
{
scanf("%d",&mem[i]);//输入n个数字
}
int sum=dfs(1);
printf("%d\n",sum);
}
return 0;
}动态规划思路：存储已知方案
注意：方案数组每次遍历完成后需要初始化
拓展：memset()函数
void *memset(void *s, int ch,size_tn);
函数解释：将s中当前位置后面的n个字节 （typedef unsigned int size_t ）用 ch 替换并返回 s 。
memset：作用是在一段内存块中填充某个给定的值，它是对较大的结构体或数组进行清零操作的一种最快方法[1]。
memset()函数原型是extern void *memset(void *buffer, int c, int count) buffer：为指针或是数组,c：是赋给buffer的值,count：是buffer的长度。
此处可以采用memset(mem,0,sizeof mem);对数组清0
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=30;
int n,k;
int mem[N];
int s[N];//记录走到当前位置的财富总和
int dfs(int x)//当前遍历到哪个店家
{int sum=0;
if(s[x]) return s[x];
if(x>n) sum=0;
else
sum=max(dfs(x+1),dfs(x+2)+mem[x]);//没被选择则是下一个数字，被选中则是隔一个数字
//sum不是累加，而是更新，所以不需要清0
s[x]=sum;//记录数据，需要更新
return sum;
}
int main()
{
scanf("%d",&k);
while(k--)//循环输入k组数据
{
scanf("%d",&n);
for(int i=1;i<=n;i++)//位置是从1开始
{
scanf("%d",&mem[i]);//输入n个数字
}
memset(s,0,sizeof s);//更新数组
int res=dfs(1);
printf("%d\n",res);
}
return 0;
}s[i]存储的是：从i店铺开始能够获取的最大价值
要实现记忆化搜索，dfs的参数就要尽可能的少，不应该把没有影响边界的参数放进来。
递推算法dp：
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=30;
int n,k;
int F1[N];
int mem[N];
int s[N];//记录走到当前位置的财富总和
int main()
{
scanf("%d",&k);
while(k--)//循环输入k组数据
{
scanf("%d",&n);
for(int i=1;i<=n;i++)//位置是从1开始
{
scanf("%d",&mem[i]);//输入n个数字
}
memset(s,0,sizeof s);//更新数组
for(int i=n;i>=1;i--)//递推是由下往上，从f[4]=0开始递推
{
if(i>n)
F1[i]=0;
else
F1[i]=max(F1[i+1],F1[i+2]+mem[i]);
}
printf("%d\n",F1[1]);
}
return 0;
}做法是1~n探查，递推返回则从n回到1
想用1-n做递推，则需要从n开始枚举
F1[i]=max(F1[i-1]，F1[i-2]+mem[i]);//当i为1，2时数组下标出现负数，下标同时加2得：
F1[i+2]=max(F1[i+1，F1[i]+mem[i]);
空间优化：
for(int i=1;i<n=;i++)
{newf=max(tmp1,tmp2+mem[i]);
tmp2=tmp1;
tmp1=newf;
}
- 使用两个变量
tmp1和tmp2来存储前一个位置的最大财富和当前位置不选择前一个位置时的最大财富。 - 通过一个循环，计算到每个位置时的最大财富，并存储在
newf中。 - 打印出最后一个位置的最大财富。