多做真题,吃透真题和背后的知识点是备考AMC8、AMC10有效的方法之一,通过做真题,可以帮助孩子找到真实竞赛的感觉,而且更加贴近比赛的内容,可以通过真题查漏补缺,更有针对性的补齐知识的短板。

今天我们继续做3道AMC8真题和2道AMC10真题,并进行详细解析。完整学习资料和信息请查看文末。
2000-2024年AMC8真题和解析:2024年第7题
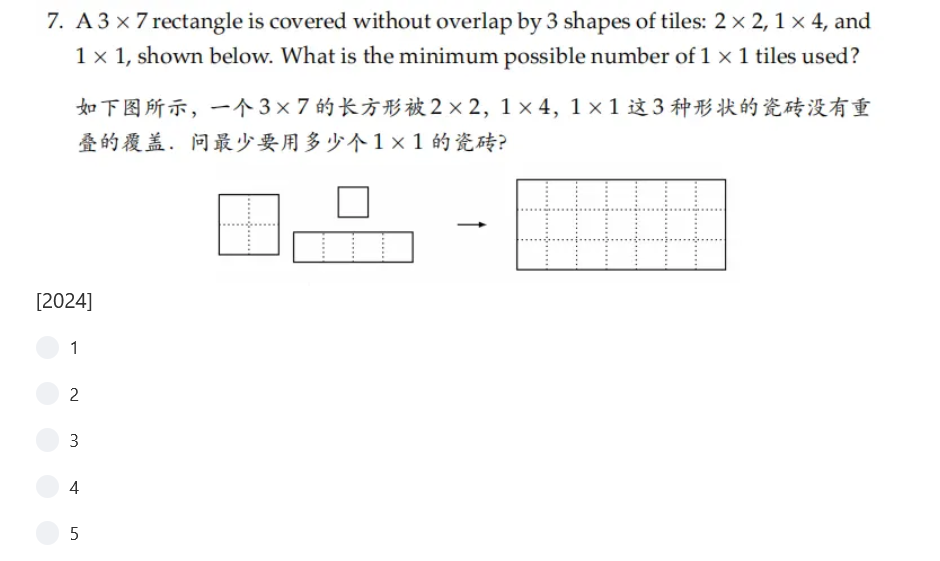
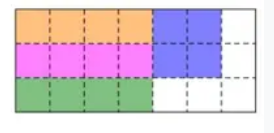
这道题的考点是平面几何,平面想象能力。要用1×1的瓷砖最少,那么其他两种形状的瓷砖就要尽可能多,如下是其中的一种拍法,还有其他拍法,但最少都要用到5个1×1的形状。所以答案选E。
2000-2024年AMC8真题和解析:2017年第20题

这道题的考点是概率+排列组合。
因为这个数是奇数,所以最后一个数字共有5种选择(1、3、5、7、9)。第一个数字现在只剩8种选择(不能是0或者和最后一个数字相同),第二个数字也只剩8种选择(不能和第一个数宇或最后一个数字相同),最后第三个数字有7种选择(不能和已经确定的其他三位的数字相同)。因为共有9000个整数,因此概率为8*8*7*5/9000=56/225,答案选B。
2000-2024年AMC8真题和解析:2009年第2题

这道题的考点是比例。
假设预计销售x辆轿车,则有4:7=28:x,解得x=49,答案选D。
提醒:这种题目不列公式,也可以直接按比例快速得出答案,因为28是4的7倍,所以最后卖出的轿车也是7的7倍=49。
2000-2023年AMC10真题和解析:2022年第7题

这道题的考点是概率,分类讨论。根据题意,原来红蓝球各1个,经过4次操作,有6个球红蓝各3个,意味着4次操作中,抽到了2个红色,2个蓝色。那么4次操作中哪2次摸到红球,需要进行分类讨论,结果为为1/5,选B。具体讨论如下:


这道题的考点是代数(解应用题),余角的概念和计算。
令这两个锐角分别是5k和4k,根据他们余角的关系,得到90-4k=2*(90-5),解得k=15。因此这两个角度数之和为5k+4k=9k=135,选C。
AMC8和AMC10的高质量、科学的备考资源,欢迎了解更多
上述在线练习题,基于认知心理学和教育学原理设计,来源于完整的历年AMC8和AMC10(包括AB卷)真题,不限设备、自动判卷、多种练习形式、每道题都有解析,并且持续更新。
这些真题的在线练习除了可以用于参加竞赛备考、反复练习,即使不参加竞赛也可促进小学、初中数学能力提升。还有配套的系统学习文档、视频资料赠送。欢迎联系我了解和获取。