🎁个人主页:我们的五年
🔍系列专栏:数据结构课程学习
🎉欢迎大家点赞👍评论📝收藏⭐文章


目录
1.二插树的概念和结构
🚗二叉树的概念:
●二叉树中所以的节点的度都小于2,也就是一个父节点最大两个子节点。
●二叉树是一种有序结构,左孩子和有孩子颠倒,二叉树是有序树。
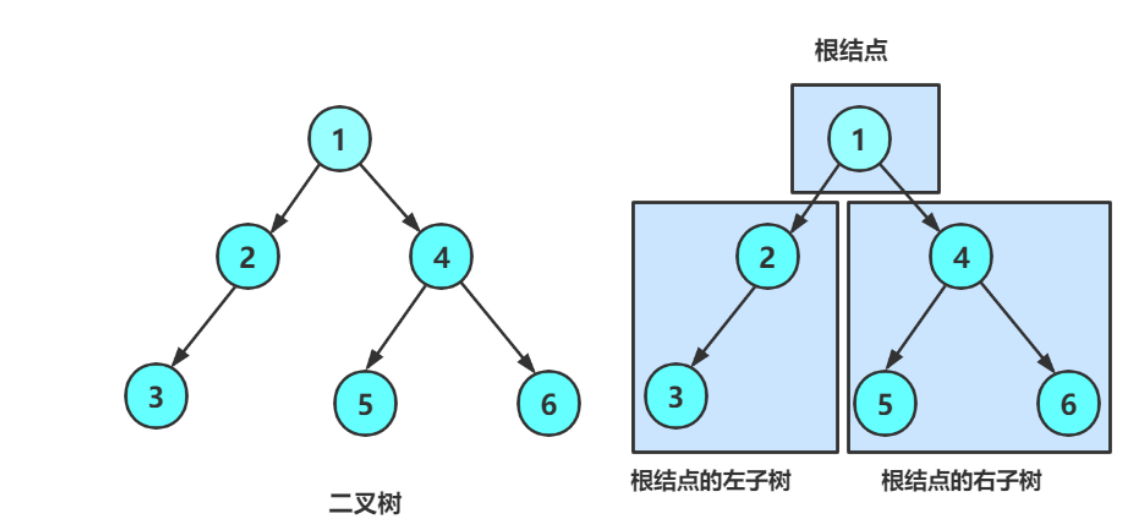
●树是递归定义的,所以二叉树也可以一直往下分,而且每一个节点最多也只能分成左右两个部分。
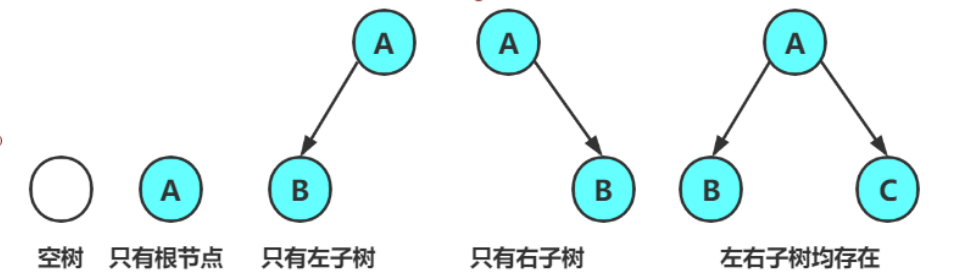
二叉树由下面几种情况组成:空树,只有根节点,只有左子树,只有有子树,左右子树
因为左右孩子不能颠倒,所以左子树和右子树是不一样的。
🚗特殊的二叉树:
可以把根节点看成第树的第1层,也可以看成树的第0层。但是把根节点看成第0层,那么是空树的时候,树的深度为-1。这样定义的话就比较别扭,所以还是把根节点定义为树的第一层。
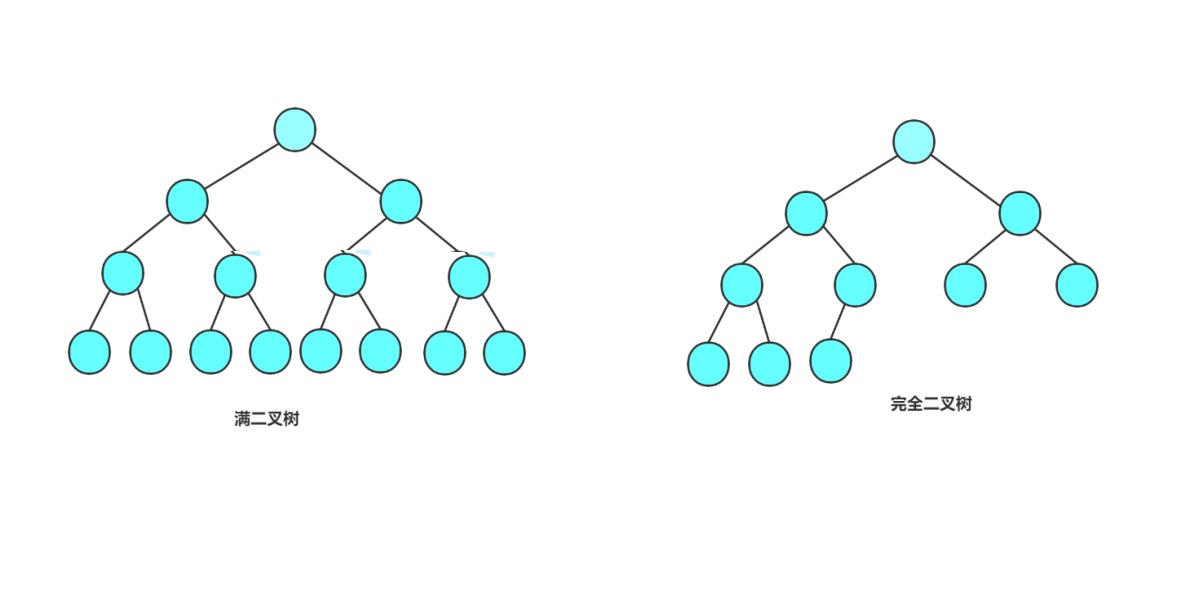
🚀满二叉树:
每一层达到最大节点数的时候,为满二叉树。也就是第n层最多的节点数为2^(n-1)个。n层的满二叉树,总节点为2^n -1个。
🚀完全二叉树:
完全二叉树可以看成是从满二叉树截取出来的,完全二叉树里的节点和满二叉树的节点一一对应。即每一层都要从最左边往右边定义,而且先是左孩子,然后再是右孩子。
🚗二叉树的性质:
规定根的节点层级为1
●一棵非空二叉树的第n层最多有2^(n-1)个节点,总节点最多为2^n-1。
●当只有根节点的时候,叶子节点为M个,度为2的节点为N个。所以只有根节点的时候,叶子节点为M=1,度为2的节点为N=0。所以M=N+1。然后在任何情况下,增加一个叶子节点,度为2的节点也会增加一个。所以二叉树中,任何非空情况下都有:
叶子节点数=度为2的节点数+1
●有N个节点,那么就有(N-1)条边。因为除了根节点以外,每增加一个节点就要增加一条边。
●具有n个结点的满二叉树的深度,h=log2(n+1)。
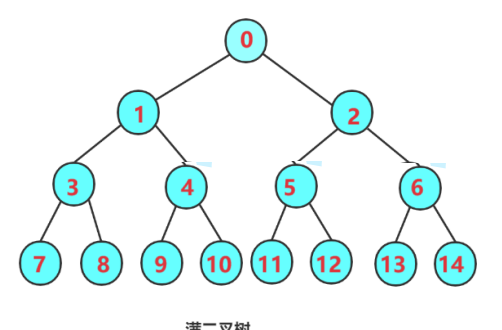
●从树从上到下,从左到右进行编号,根节点编号为0,一共有N个节点,最大序号为N-1那么有下面结论:
1.除了根节点以外,其他的都有父节点,那么第i个节点的父节点的序号为:(i-1)/2。
2.如果第i个节点,2*i+1<N,那么2*i+1为i节点的左孩子,如果大于等于N,那么没有左孩子。
3.如果第i个节点,2*i+2<N,那么2*i+2为i节点的右孩子,如果大于等于N,那么没有右孩子。
🚗二叉树的几个理论题:
1. 某二叉树共有 399 个结点,其中有 199 个 度为 2 的结点 ,则该二叉树中的 叶子结点数 为( B)A 不存在这样的二叉树B 200C 198D 199解:B。因为除了空树以外,其他情况下都有: 叶子节点数=度为2的节点数+1 ,度为2的节点数为199,那么叶子节点为200。
2.下列数据结构中,不适合采用顺序存储结构的是(A )
A 非完全二叉树B 堆C 队列D 栈解:A。因为如果连完全二叉树都不是,定义的顺序就不是满足从左到右,从上到下。这样用顺序存储就不太合适,如果是完全二叉树,用数组存储还是可以的。
3.在具有 2n 个结点的完全二叉树中,叶子结点个数为(B )A nB n+1C n-1D n/2解:B。因为节点数是2n个,是偶数个,又是完全二叉树,所以只有一个节点的度为1,其他的要么是叶子节点,要么是度为2的节点,所以有: 度为2的节点+叶子节点+1=叶子节点-1+叶子节点+1=2*叶子节点=2n,所以叶子节点为n个。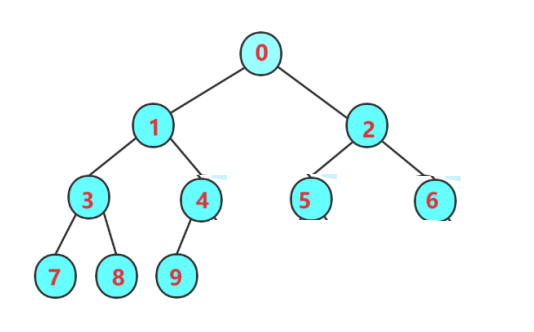
4.一棵完全二叉树的结点数位为531个,那么这棵树的高度为( B)A 11B 10C 8D 12解:B。当高度为9的满二叉树节点总数为2^9-1=511,高度为10的满二叉树的总节点为2^10-1=1023,531在511和1023之间,所以这棵树的高度为10。
5.一个具有767个结点的完全二叉树,其叶子结点个数为(B)A 383B 384C 385D 386解:B。767个节点,与第三题差不多,但是是奇数个节点,那么所以节点的度都是2,所以有: 度为2的节点数+叶子节点数=767,度为2的节点数+1=叶子节点数。所以叶子节点*2-1=767,所以叶子节点为384。
🚗二叉树的存储结构:
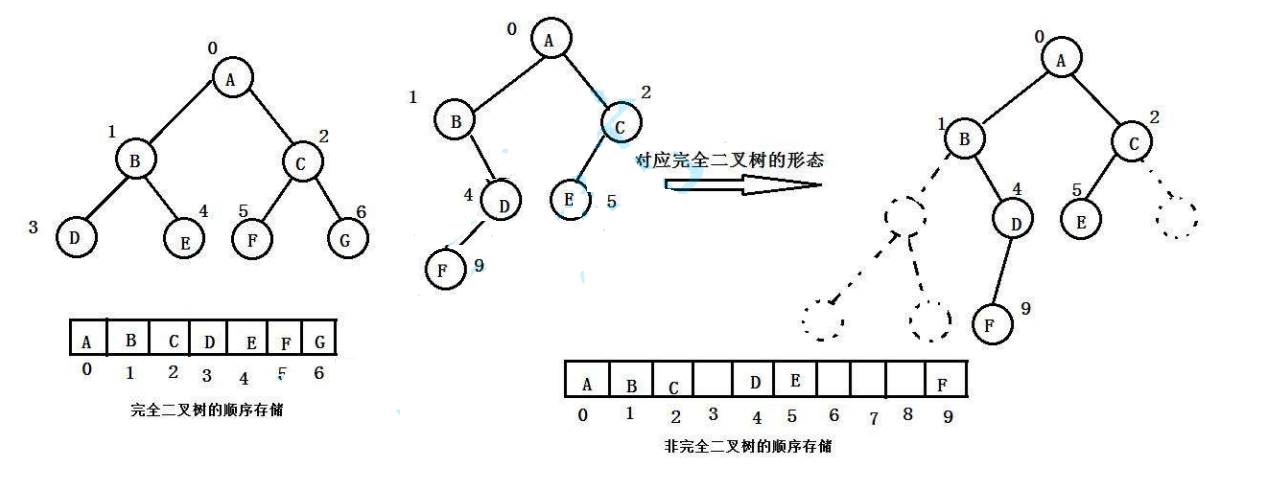
1.顺序存储:
顺序存储时使用数组来存储,完全二叉树适合用数组存储。这时候在物理层面上看时数组,从逻辑上看是一课二叉树。不是完全二叉树会存在空间浪费。
2.链式存储:
用链表来存储二叉树,即用链的逻辑关系来存储二叉树。链表的结构里一般存这数据,左孩子的地址,右兄弟的地址。
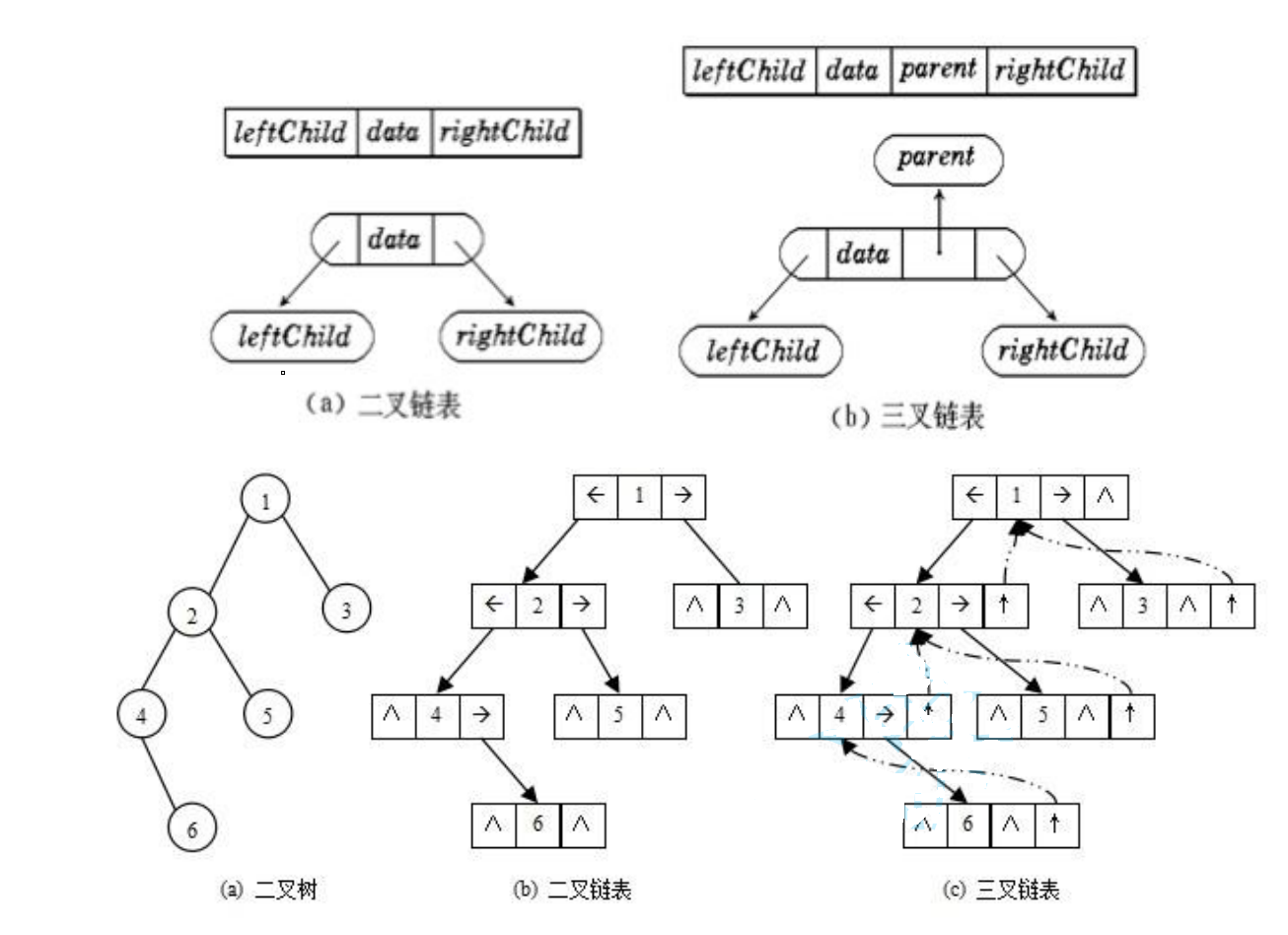
//二叉链
struct BinaryTreeNode {
int x;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
};
//三叉链
struct BinaryTreeNode {
int x;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
struct BinaryTreeNode* parent;
};2.堆:
1.堆是一棵完全二叉树。
2.堆的父节点总是大于等于或者小于等于子节点。
二叉树基本的函数:
🏝头文件和堆的结构定义:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct HP {
HPDataType* a;
int size;
size_t capacity;
}HP;
//堆的初始化
void HPInit(HP* php);
//堆的销毁
void HPDestroy(HP* php);
//堆的插入,一小堆为例,小堆:父节点都小于子节点
void HPPush(HP* php, HPDataType x);
//取堆顶元素,小堆取的是最小值,大堆取的是最大值
HPDataType HPTop(HP* php);
//删除堆顶的数据
void HPPop(HP* php);
//判空函数
bool HPEmpty(HP* php);🏝1.初始化堆:
void HPInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}🏝2.堆的销毁:
//堆的销毁
void HPDestroy(HP* php)
{
assert(php);
free(php->a);
php->capacity = php->size = 0;
}🏝3.堆的插入:
向上调整函数是往上遍历,当父节点大于子节点,就进行交换数据,循环结束的条件是当孩子节点到达根节点,一直这样循环就可以符合小堆的结构。每次调整都把最小的往上移。
//交换两个数的函数
void Swap(HPDataType* px, HPDataType* py)
{
HPDataType tmp = *px;
*px = *py;
*py = tmp;
}
//向上调整函数
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0) //如果循环的条件为parent>=0,循环也会巧合的结束,但是这种情况是不可取的
{
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}
//堆的插入,以小堆为例,小堆:父节点都小于子节点
void HPPush(HP* php, HPDataType x)
{
assert(php);
if (php->capacity == php->size)
{
size_t newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = realloc(php->a, newcapacity * sizeof(HPDataType));
if (tmp == NULL)
{
perror("realloc");
return;
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size++] = x;
AdjustUp(php->a,php->size - 1);
}🏝4.删除堆顶元素:
//交换两个数的函数
void Swap(HPDataType* px, HPDataType* py)
{
HPDataType tmp = *px;
*px = *py;
*py = tmp;
}
//向下调整
void AdjustDown(HPDataType* a, int size)
{
//假设法,先假设左孩子比右孩子小
int parent = 0;
int child = parent* 2 + 1;
while (child < size)
{
if (child+1<size&&a[child + 1] < a[child])
{
++child;
}
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//删除堆顶的数据
void HPPop(HP* php)
{
//先交换堆顶元素和堆的最后一个元素
php->size--;
Swap(&php->a[0], &php->a[php->size]);
AdjustDown(php->a, php->size);
}🏝5.取堆顶元素和判空元素:
//删除堆顶的数据
void HPPop(HP* php)
{
//先交换堆顶元素和堆的最后一个元素
php->size--;
Swap(&php->a[0], &php->a[php->size]);
AdjustDown(php->a, php->size);
}
//判空函数
bool HPEmpty(HP* php)
{
assert(php);
return php->size == 0;
}