目录
04 数组+双指针
数组中的指针称为索引。
双指针有三种技巧:快慢指针、左右指针、滑动窗口
所谓左右指针,就是两个指针相向而行或者相背而行;而快慢指针,就是两个指针同向而行,一快一慢。
接下来用经典题来讲解。
PS.力扣上面的题目字儿好多,我觉得先看题目标题,然后再看例子,最后看题目,这样的顺序会快一点理解吧。看不懂答案的可以参考labuladong的算法笔记以及题解,还不懂的就问chatgpt。
1.快慢指针(一前一后)
[1]删除有序数组中的重复项
给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums,使nums的前k个元素包含唯一元素,并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。 - 返回
k。
示例 1:
输入:nums = [1,1,2] 输出:2, nums = [1,2,_] 解释:函数应该返回新的长度2,并且原数组 nums 的前两个元素被修改为1,2。不需要考虑数组中超出新长度后面的元素。
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
slow, fast = 0, 1
while fast < len(nums): #注意是<
if nums[fast] != nums[slow]:
slow = slow + 1
nums[slow] = nums[fast]
fast = fast + 1
return slow + 1
思路提示: 首先,我们知道数组nums是升序的,而且我们只能在原地修改nums数组,不能创建新的数组空间来存储删除重复出现的元素后的结果。我们需要一边遍历数组查找相同元素,一边在对比发现不同元素时修改数组元素,那么我们可以考虑双指针法的快慢指针了,定义slow和fast作为指针,初始化时指针slow指向数组的起始位置(nums[0]),指针fast指向指针slow的后一个位置(nums[1])。随着指针fast不断向后移动,将指针fast指向的元素与指针slow指向的元素进行比较:
如果nums[fast] ≠ nums[slow],那么nums[slow + 1] = nums[fast];
如果nums[fast] = nums[slow],那么指针fast继续向后查找;
[2]移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
输入:nums = [3,2,2,3], val = 3 输出:2, nums = [2,2] 解释:函数应该返回新的长度2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
思路:如果 fast 遇到值为 val 的元素,则直接跳过,否则就赋值给 slow 指针,并让 slow 前进一步。
相当于slow指针把不等于 val 的元素提到前面了。
def removeElement(nums: List[int], val: int) -> int:
fast, slow = 0, 0
while fast < len(nums):
if nums[fast] != val:
nums[slow] = nums[fast]
slow += 1
fast += 1
return slow
不需要考虑数组中超出新长度后面的元素,按照示例一,最后的结果是[2, 2, 2, 3]
2.左右指针(一左一右)
[1] 二分查找
二分查找真正的坑在于到底要给 mid 加一还是减一,while 里到底用 <= 还是 <。
典型题:搜索一个数,如果存在,返回其索引,否则返回 -1。
def binarySearch(nums:List[int], target:int) -> int:
left = 0;
right = len(nums) - 1; # 注意
while(left <= right):
mid = left + (right - left) // 2; # 防止整型溢出
if(nums[mid] == target):
return mid;
elif(nums[mid] < target):
left = mid + 1; # 注意
elif(nums[mid] > target):
right = mid - 1; # 注意
return -1;
(1)第一个注意的点:这里将 right 初始化为 len(nums) - 1,即列表 nums 的最后一个元素的索引。
(2)第二个注意的点:
`mid = left + (right - left) // 2` 是一种常见且有效的计算中间值的方式,其背后有以下几个原因:
1.避免整数溢出:
在使用传统的 `(left + right) // 2` 计算中间值时,如果 `left` 和 `right` 都是很大的整数,那么它们相加可能会导致整数溢出,产生错误的结果。为了避免这种情况,我们可以将 `(right - left)` 替换为 `(right - left) // 2`,这样可以确保计算中间值时不会溢出。
2.向下取整:
当 `(right - left)` 是奇数时,除以 2 得到的结果会向下取整,即舍弃小数部分。这种方式确保了中间值 `mid` 始终是左半部分的最后一个元素,而不是右半部分的第一个元素。
(3)第三、四个注意的点:
[left, right]这个区间找不到,那就去搜索区间 [left, mid-1] 或者区间 [mid+1, right] 对不对?因为 mid 已经搜索过,应该从搜索区间中去除。
(4)while 循环的条件中是 <=,相当于两端都闭区间 [left, right]
寻找左侧边界和右侧边界的请见:
我写了首诗,把二分搜索算法变成了默写题 | labuladong 的算法笔记
这个总结的代码挺好,可以直接背
# 注意:python 代码由 chatGPT🤖 根据我的 java 代码翻译,旨在帮助不同背景的读者理解算法逻辑。
# 本代码不保证正确性,仅供参考。如有疑惑,可以参照我写的 java 代码对比查看。
def binary_search(nums: List[int], target: int) -> int:
# 设置左右下标
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# 找到目标值
return mid
# 没有找到目标值
return -1
def left_bound(nums: List[int], target: int) -> int:
# 设置左右下标
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# 存在目标值,缩小右边界
right = mid - 1
# 判断是否存在目标值
if left < 0 or left >= len(nums):
return -1
# 判断找到的左边界是否是目标值
return left if nums[left] == target else -1
def right_bound(nums: List[int], target: int) -> int:
# 设置左右下标
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# 存在目标值,缩小左边界
left = mid + 1
# 判断是否存在目标值
if right < 0 or right >= len(nums):
return -1
# 判断找到的右边界是否是目标值
return right if nums[right] == target else -1
[2] 两数之和
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
left, right = 0, len(nums) - 1
while left < right:
sum = nums[left] + nums[right]
if sum == target:
# 题目要求的索引是从 1 开始的
return [left + 1, right + 1]
elif sum < target:
left += 1 # 让 sum 大一点
else:
right -= 1 # 让 sum 小一点
return [-1, -1]经典题:反转数组、回文串判断,都是类似的技巧
[3] 最长回文串
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd" 输出:"bb"
解决该问题的核心是从中心向两端扩散的双指针技巧。
具体思路是,构建一个【从中心往两边扩散】的函数——扩散的条件是,不超出边界且扩散的两边的元素相等,函数返回回文字符串。基于构建的函数,以此判断s中所有的位置,用一个res保留最长的结果。
大白话是,每个位置都判断下,以该位置为中心的回文串最长为多少,遍历一遍,保留最长的那个。
其中有一个细节,中心元素需要区分1个或者2个的情况(回文串中元素个数为奇数/偶数)
如果回文串的长度为奇数,则它有一个中心字符;如果回文串的长度为偶数,则可以认为它有两个中心字符。
class Solution:
def longestPalindrome(self, s: str) -> str:
res = ''
for i in range(len(s)): #i从0开始
s1 = self.expandAroundCenter(s, i, i)
s2 = self.expandAroundCenter(s, i, i + 1)
if len(s1) > len(res):
res = s1
if len(s2) > len(res):
res = s2
return res
def expandAroundCenter(self, s, left, right):
while left >= 0 and right <= len(s) - 1 and s[left] == s[right]:
left -= 1
right += 1
return s[left + 1: right]
(1)为什么返回 s[left + 1: right]?
因为在 while 循环结束后,left 和 right 分别指向不满足回文条件的两个字符,但是这两个字符并不属于回文子串内。所以,我们需要返回的是从 left 的下一个位置到 right 的前一个位置的子串,即 s[left + 1: right],这个子串才是我们找到的最长回文子串。切片的右边界是开区间。
在 expandAroundCenter 方法中,使用两个指针 left 和 right 分别从当前字符向左右两边扩展,直到不再满足回文条件(即 s[left] != s[right]),然后返回扩展后的回文子串。
(2)使用 i 和 i+1 的方式来调用 expandAroundCenter 函数,可以区分奇数长度和偶数长度的回文子串:
当以
i作为中心时,expandAroundCenter函数会考虑当前字符s[i]为中心的奇数长度的回文子串。当以
i和i+1作为中心时,expandAroundCenter函数会考虑由相邻字符s[i]和s[i+1]组成的偶数长度的回文子串。在
longestPalindrome方法中,比较得到的两种情况下的回文子串的长度,将较长的更新为res。
3.滑动窗口
滑动窗口算法的思路:维护一个窗口,不断滑动,然后更新答案
用来解决的问题:子数组问题或者子串问题
框架如下:
首先是窗口向右滑动,寻找一个「可行解」,
然后窗口的左端向右走,窗口整体是缩小的,优化这个「可行解」,
直到缩小到不能缩小为止,找到最优解。
def slidingWindow(s: str):
# 用合适的数据结构记录窗口中的数据,根据具体场景变通
# 比如说,我想记录窗口中元素出现的次数,就用 map
# 我想记录窗口中的元素和,就用 int
window = dict()
left = 0
right = 0
while right < len(s):
# c 是将移入窗口的字符
c = s[right]
window[c] = window.get(c, 0) + 1
# 增大窗口
right += 1
# 进行窗口内数据的一系列更新
#...
#/*** debug 输出的位置 ***/
# 注意在最终的解法代码中不要 print
# 因为 IO 操作很耗时,可能导致超时
# print(f"window: [{left}, {right})")
# 判断左侧窗口是否要收缩
while left < right and "window needs shrink":
# d 是将移出窗口的字符
d = s[left]
window[d] -= 1
if window[d] == 0:
del window[d]
# 缩小窗口
left += 1
# 进行窗口内数据的一系列更新
#...
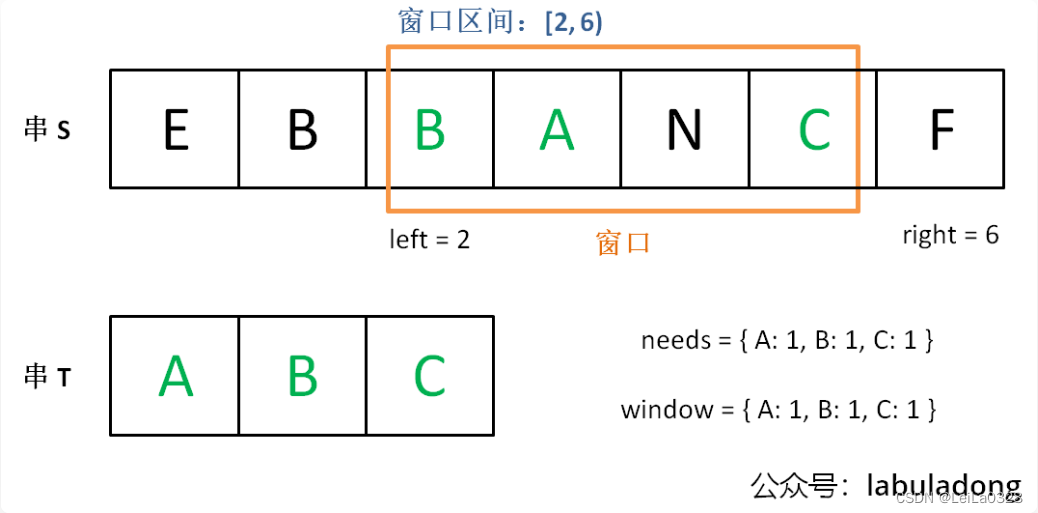
[1]最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
- 对于
t中重复字符,我们寻找的子字符串中该字符数量必须不少于t中该字符数量。 - 如果
s中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC" 解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
示例 2:
输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中, 因此没有符合条件的子字符串,返回空字符串
前置知识:在Python中,哈希表的实现是通过内置的字典(dict)数据类型来完成的。
# 使用字面量表示法创建哈希表
my_dict = {"apple": 3, "banana": 2, "orange": 5}
# 使用 dict() 构造函数创建哈希表
my_dict = dict(apple=3, banana=2, orange=5)
# 查找键对应的值
print(my_dict["apple"]) # 输出:3
# 添加新的键值对
my_dict["grape"] = 4
# 删除指定键值对
del my_dict["banana"]
# 判断键是否存在
if "orange" in my_dict:
print("Yes")
else:
print("No")
class Solution:
def minWindow(self, s: str, t: str) -> str:
from collections import defaultdict
#初始化
need, window = defaultdict(int), defaultdict(int)
for c in t:
need[c] += 1
left, right = 0, 0
valid = 0 #下文有注释
start, length = 0, float('inf')
#窗口向右滑动
while right < len(s):
# c 是将移入窗口的字符
c = s[right]
# 扩大窗口
right += 1
# 进行窗口内数据的一系列更新
if c in need:
window[c] += 1
if window[c] == need[c]:
valid += 1
#内嵌循环,判断左侧窗口是否要收缩
while valid == len(need):
# 在这里更新最小覆盖子串
if (right - left) < length:
start = left
length = right - left
#收缩窗口,并更新相应字符的计数和 valid 值
# d 是将移出窗口的字符
d = s[left]
# 缩小窗口
left += 1
# 进行窗口内数据的一系列更新
if d in need:
if window[d] == need[d]:
valid -= 1
window[d] -= 1
# 返回最小覆盖子串
return "" if length == float('inf') else s[start:start + length]
1.使用双指针 left 和 right 维护一个滑动窗口,初始时都指向字符串的开头。
2.`valid`、`start` 和 `length` 的作用如下:
`valid`:用于记录当前窗口中已经包含了字符串 `t` 中的所有字符的数量。当 `valid` 的值等于 `len(need)`(即 `need` 字典中键值对的数量)时,表示当前窗口已经包含了字符串 `t` 中的所有字符。
`start` 和 `length`:用于记录找到的最小覆盖子串的起始索引和长度。在遍历过程中,当找到一个满足条件的最小覆盖子串时,会更新 `start` 和 `length` 的值,以便最后返回最小覆盖子串。
因此,`valid` 用于辅助判断当前窗口是否满足条件,而 `start` 和 `length` 用于记录最终的最小覆盖子串的位置和长度。
3.float('inf') 用于初始化 length 变量,将其设为正无穷大。这样,在查找最小覆盖子串时,如果 length 的值没有被更新,就表示没有找到满足条件的子串,因此返回空字符串。
4.在while right < len(s)循环内部有一个内嵌的 while valid == len(need): 循环,这个循环表示当窗口中包含了字符串 t 中的所有字符时,需要进行窗口的收缩。
5.if (right - left) < length: start = left length = right - left
right - left是当前窗口的长度。length是迄今为止找到的最小覆盖子串的长度,初始值为float('inf')(表示无穷大)。- 这个条件判断当前窗口长度是否小于已记录的最小覆盖子串长度。
[2]其他经典题目
滑动窗口算法核心代码模板 | labuladong 的算法笔记
滑动窗口遇到子数组/子串相关的问题,你只要能回答出来以下几个问题,就能运用滑动窗口算法:
1、什么时候应该扩大窗口?
通常在以下情况下你需要扩大窗口:
- 当前窗口不满足题目给定的条件,需要包含更多的元素来使窗口有效。
- 你还没有遍历完所有可能的子数组/子串,所以需要继续向右移动窗口的右边界。
具体的判定标准取决于问题的要求。例如,在找到最长的无重复子串时,当遇到一个新的字符且没有重复时,应扩大窗口。
2、什么时候应该缩小窗口?
通常在以下情况下你需要缩小窗口:
- 当前窗口已经满足题目给定的条件,但可能可以找到更优解(如更短的子数组)。
- 需要从窗口中移除一些元素以使窗口重新变得有效或者继续寻找其他可能的解。
具体情况依赖于问题的具体要求。例如,在找到和为某个值的最短子数组时,当当前窗口和大于目标值时,应缩小窗口。
3、什么时候应该更新答案?
- 当前窗口满足题目给定的条件,并且此时需要记录或更新你找到的最优解。
- 找到一个比之前记录的解更优的解。
本文参考了labuladong的算法笔记,以及力扣上一些大佬的题解,因为引用的太多,故不一一注释references了,如果作者介意的话请联系我加上出处~
全文仅作个人学习笔记,记录和思考,不作商业目的。