碰撞检测 | 1D/2D碰撞时间TTC模型理论推导(附Python实现)

0 专栏介绍

🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

🚀详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

1 什么是碰撞时间？

碰撞时间(Time-to-Collision, TTC)是驾驶行为研究中常用的重要概念，指交通流上两个物体在当前运动状态下的预测性碰撞时间，用于评估物体间的接近程度、交互强度和潜在的碰撞风险，常用于交通流畅性和安全性分析的重要风险指标，并为轨迹规划和决策提供量化依据。举例而言，在自动辅助驾驶系统(Autonomous Driving Assistance System, ADAS)中，基于TTC的预警流程为：实时地计算出本车与障碍车的TTC指标，当TTC小于前向碰撞预警阈值时，系统采用视觉、听觉或触觉向驾驶员报警；当TTC小于自动紧急制动阈值时，系统以一定的减速度采取紧急制动。

2 一维TTC计算模型

考虑自车的前方车辆且假设两车加速度恒定，基于运动学公式，两车经过相同的时间$t$的实时位置为

$$\{\begin{array}{l}{x}_1^{\ast }=x_1+v_{1}t+\frac{1}{2}{a}_1{t}^2\\ x_2^{\ast }=x_2+v_{2}t+\frac{1}{2}{a}_2{t}^2\end{array}\left(x_1<x_2\right)$$

令二者之差为安全距离$d=x_2^{\ast }-x_1^{\ast }$，则解得二次方程为

$$ttc=\{\begin{array}{l}\frac{x_2-x_1-d}{v_1-v_2},a_1=a_2\\ \frac{-\left(v_1-v_2\right)+\sqrt{{\left(v_1-v_2\right)}^2+2\left(a_1-a_2\right)\left(x_2-x_1-d\right)}}{a_1-a_2},a_1\ne a_2\end{array}$$

考虑到有意义的$ttc>0$，可知

• 当$a_1=a_2$时，自车速度需要大于前车$v_1>v_2$；
• 当$a_1\ne a_2$时，自车加速度需要大于前车$a_1>a_2$，即加速更快或减速更慢；

才会进入TTC预警流程。上述公式适合两车均在运动过程时的TTC计算，在前方减速行驶车辆追尾测试中，若两车最短距离发生在前车刹停后，则需要对上述公式进行修正

$$tt{c}^{\prime }=\{\begin{array}{l}\frac{x_2-x_1-d+\left|\frac{v_2^2}{2a_2}\right|}{v_1},a_1=a_2\\ \frac{-v_1+\sqrt{v_1^2+2a_1\left(x_2-x_1-d+\left|\frac{v_2^2}{2a_2}\right|\right)}}{a_1},a_1\ne a_2\end{array}$$

3 二维TTC计算模型

在一维情况下，TTC通过将相对碰撞距离(Distance-to-Collision, DTC)除以相对速度来计算。在二维情况下，DTC相应地指的是车辆包围盒沿其相对速度方向的最小距离。如果相对运动减小了距离，则说明它们彼此靠近，存在潜在的碰撞；反之则不存在。

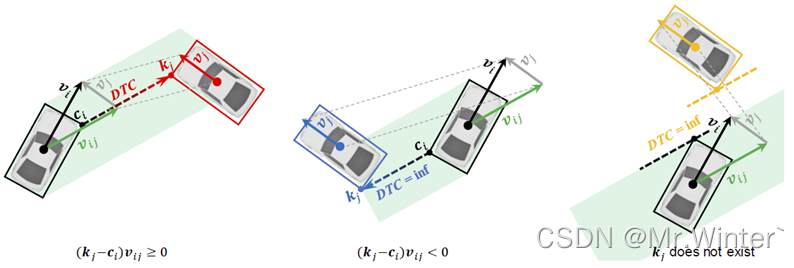
具体地，如图所示，设$i$是目标车辆，$j$是交互车辆，相应的包围盒角点集合为$C_i$和$C_j$，边界集合为$B_i$和$B_j$。对每个目标车辆的角点

$${\mathbf{c}}_{i,m}\in C_i\left(m=1,2,3,4\right)$$

沿着相对速度方向${\mathbf{v}}_{ij}={\mathbf{v}}_i-{\mathbf{v}}_j$延长，求该直线和车辆$j$包围盒每条直线边的交点集合$K_j$，则

$$d_{im\to jn}=\{\begin{array}{l}\Vert {\mathbf{k}}_{j,n}-{\mathbf{c}}_{i,m}\Vert ,{\left({\mathbf{k}}_{j,n}-{\mathbf{c}}_{i,m}\right)}^T{\mathbf{v}}_{ij}⩾0\\ \mathrm{i}\mathrm{n}\mathrm{f},{\left({\mathbf{k}}_{j,n}-{\mathbf{c}}_{i,m}\right)}^T{\mathbf{v}}_{ij}<0\mathrm{o}\mathrm{r}\nexists {\mathbf{k}}_{j,n}\in K_j\cap B_j\ne \oslash \end{array}$$

遍历所有的${\mathbf{c}}_{i,m}\in C_i$和${\mathbf{k}}_{j,n}\in K_j$可得${\mathbf{D}}_{i\to j}$，从而碰撞距离

d t c = min ⁡ { min ⁡ { D i → j } , min ⁡ { D j → i } } dtc=\min \left\{ \min \left\{ \boldsymbol{D}_{i\rightarrow j} \right\} ,\min \left\{ \boldsymbol{D}_{j\rightarrow i} \right\} \right\} dtc=min{min{Di→j​},min{Dj→i​}}

以及碰撞时间

$$ttc=\{\begin{array}{l}\frac{dtc}{\Vert {\mathbf{v}}_{ij}\Vert },dtc\ne \mathrm{i}\mathrm{n}\mathrm{f}\\ \mathrm{i}\mathrm{n}\mathrm{f},dtc=\mathrm{i}\mathrm{n}\mathrm{f}\end{array}$$

4 算法仿真

考虑到一维TTC计算是简单的代数公式，这里仅给出2D TTC计算的代码。核心的计算目标车辆$i$和交互车辆$j$的代码如下所示

def TTC_ij(samples):
    point_i1, point_i2, point_i3, point_i4, point_j1, point_j2, point_j3, point_j4 = getpoints(samples)
    direct_v = (samples[['vx_i','vy_i']].values - samples[['vx_j','vy_j']].values).T

    dist_mat = []
    leaving_mat = []
    for point_line_start in [point_i1,point_i2,point_i3,point_i4]:
        for edge_start, edge_end in zip([point_j1, point_j3, point_j1, point_j2],[point_j2, point_j4, point_j3, point_j4]):
            point_line_end = point_line_start+direct_v
     
            ist = intersect(line(point_line_start, point_line_end), line(edge_start, edge_end))
            ist[:,~ison(edge_start, edge_end, ist)] = np.nan

            dist_ist = np.sqrt((ist[0]-point_line_start[0])**2+(ist[1]-point_line_start[1])**2)
            dist_ist[np.isnan(dist_ist)] = np.inf
            dist_mat.append(dist_ist)
            leaving = direct_v[0]*(ist[0]-point_line_start[0]) + direct_v[1]*(ist[1]-point_line_start[1])
            leaving[leaving>=0] = 10
            leaving[leaving<0] = 1
            leaving_mat.append(leaving)

    dist2overlap = np.array(dist_mat).min(axis=0)
    TTC = dist2overlap/np.sqrt((samples.vx_i-samples.vx_j)**2+(samples.vy_i-samples.vy_j)**2)
    leaving = np.nansum(np.array(leaving_mat),axis=0)
    TTC[leaving<10] = np.inf
    TTC[(leaving>10)&(leaving%10!=0)] = -1

    return TTC

• 一维案例

  两辆车的尺寸均为3m长、1m宽且均沿正前方行驶，前车位于(2,1)坐标处且速度为1m/s，后车位于(-2,1)且速度为3m/s，计算碰撞时间

  test_sampe = pd.DataFrame(
      data=np.array([
          2, 1, 1, 0, 1, 0, 3, 1, -2, 1, 3, 0, 1, 0, 3, 1
      ]).reshape(1, 16),
      columns=[
          "x_i", "y_i", "vx_i", "vy_i", "hx_i", "hy_i", "length_i", "width_i",
          "x_j", "y_j", "vx_j", "vy_j", "hx_j", "hy_j", "length_j", "width_j"
      ]
  )
  
  print(TTC(test_sampe, toreturn="values"))
  
  >>> TTC=0.5 s
  

• 二维案例
  两辆车的尺寸均为3m长、1m宽，前车位于(2,1)坐标处，速度为1m/s且沿正前方行驶；后车位于(2,1-)，速度为1m/s且沿前方45°行驶，计算碰撞时间

  test_sampe = pd.DataFrame(
      data=np.array([
          2, 1, 1, 0, 1, 0, 3, 1, 2, -2, 1, 1, 1, 1, 3, 1
      ]).reshape(1, 16),
      columns=[
          "x_i", "y_i", "vx_i", "vy_i", "hx_i", "hy_i", "length_i", "width_i",
          "x_j", "y_j", "vx_j", "vy_j", "hx_j", "hy_j", "length_j", "width_j"
      ]
  )
  
  print(TTC(test_sampe, toreturn="values"))
  
  >>> TTC=1.085786 s
  

完整工程代码请联系下方博主名片获取

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …