决策树
概念
是一种树形结构
树中每个内部节点表示一个特征上判断
每个分支代表一个判断结果输出
每个叶子节点代表一种分类结果
决策树建立过程
特征选择:选取有较强分类能力的特征
决策树生成:根据选择特征生成决策树
决策树也易过拟合,采用剪枝方式缓解过拟合
决策树分类
ID3决策树
信息熵
信息论中代表随机变量不确定度的度量
熵值越大,数据不确定性越高,信息也越多
熵值越小,数据不确定性越低
计算方法

信息增益
特征a对训练数据集D信息增益g(D,a),定义为集合D的熵H(D)与特征a给定条件下D的熵H(D|a)之差
数学公式
g(D,A) = H(D)-H(D|A)
信息增益 = 熵-条件熵
条件熵
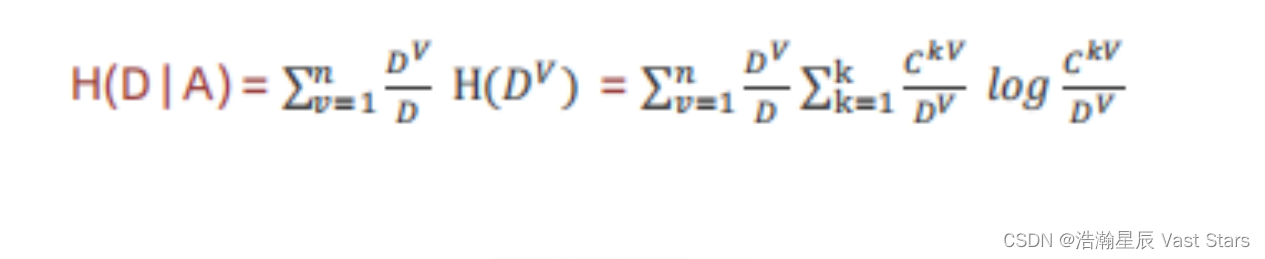
ID3决策树构建流程
1.计算每个特征信息增益
2.使用信息增益最大特征将数据集拆分为子集
3.使用该特征(信息增益最大特征)作为决策树一个节点
4.使用剩余特征对子集重复上述(1,2,3)过程
C4.5
ID树不足
偏向于选择种类较多特征作为分裂依据
信息增益率
信息增益率 = 信息增益/特征熵
计算方式
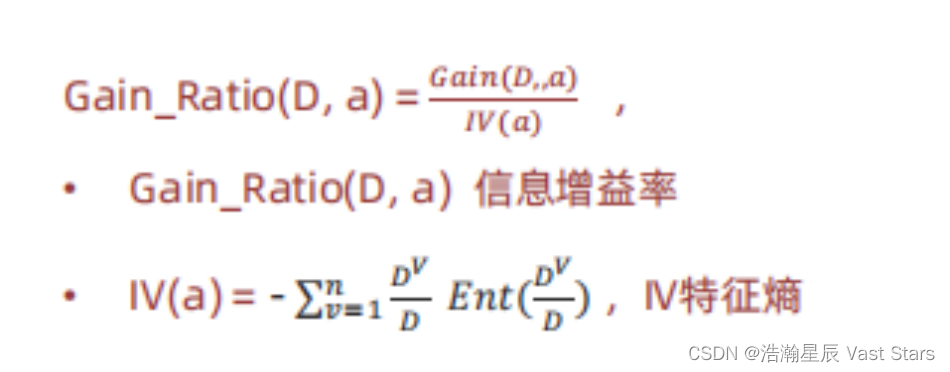
信息增益率本质
特征信息增益 ÷ 特征内在信息
相当于对信息增益进行修正,增加一个惩罚系数
特征取值个数较多时,惩罚系数较小,反之,较大
惩罚系数:数据集D以特征a作为随机变量熵的倒数
CART决策树
概念
是一种决策树模型,它即可以用于分类,也可用于回归
Cart回归树使用的是
平方误差最小化策略Cart分类生成树采用的
基尼指数最小化策略
基尼值:Gini(D)
概念
从数据集D中随机抽取两个样本,其类别标记不一致概率。故,Gini(D)值越小,数据集D纯度越高
计算方法
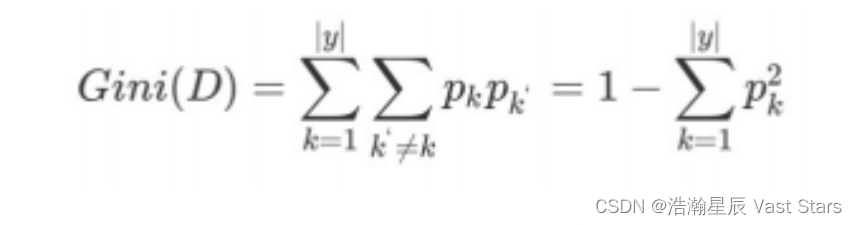
基尼指数:Gini_index (D)
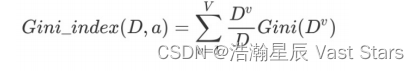
概念
选择使划分后基尼系数最小属性作为最优化分属性
计算方法
注意
信息增益(ID3)、信息增益率值越大(C4.5),则说明优先选择该特征
基尼指数越小(cart),则说明优先选择该特征
三者对比
名称 提出时间 分支方式 特点 ID3 1975 信息增益 1.ID3只能对离散属性数据集构成决策树
2.倾向于选择取值较多属性
C4.5 1993 信息增益率 1.缓解了ID3分支过程中总喜欢偏向选择值较多属性
2.可处理连续数值型属性,也增加了对缺失值处理方法 3.只适合于能够驻留于内存的数据集,大数据集无能为力
CART 1984 基尼指数 1.可以进行分类和回归,可处理离散/连续属性
2.采用基尼指数,计算量减少 3.一定是二叉树
CART回归树
决策树API
class sklearn.tree.DecisionTreeClass(criterion='gini',max_depth=None,random_state=None)
Criterion:特征选择标准
gini或entropy,前者代表基尼指数,后者代表信息增益,默认gini,即CART算法
min_samples_split:内部节点再划分所需最小样本数
min_samples_leaf:叶子节点最少样本数
max_depth:决策树最大深度
CART分类树预测输出是一个离散值,而CART回归树预测输出的是连续值
CART分类树使用基尼指数作为划分、构建树依据,CART回归树使用的平方损失
分类树使用叶子节点多数类别作为预测类别,回归树则采用叶子节点里均值作为预测输出
决策树剪枝
概念
防止决策树过拟合的一种正则化方法,提高其泛化能力
剪枝
将子树节点全部删掉,使用叶子节点来替换
剪枝方法
预剪枝
在决策树生成过程中,对每个节点在划分前线进行估计
若当前节点划分不能提高决策树泛化性能,则停止划分并将当前节点标记为叶节点
后剪枝
先从训练集生成一颗完整的决策树,然后自底向上地对非叶节点进行考察
若将该节点对应的子树替换为叶节点能带来决策树泛化性能提升
则将该子树替换为叶节点
决策树正则化与剪枝对比
| 预剪枝 | 后剪枝 | |
|---|---|---|
| 优点 | 预剪枝使决策树很多分支没有展开 不单降低了过拟合风险,还减少了决策树训练,测试时间开销 | 比预剪枝保留了更多分支 一般情况下,后剪枝决策树欠拟合风险很小 泛化性能往往优于预剪枝 |
| 缺点 | 有些分支当前划分虽不能提升泛化性能 但后续划分却有可能导致性能显著提升 从而带来欠拟合风险 | 后剪枝先生成,后剪枝。 自底向上对树中所有非叶子节点进行考察<br /训练时间开销比未剪枝决策树和预剪枝决策树都要大很多 |