【高级机器学习理论】变分推理

关键词：Variational Inference

一、说明

   我们生活在量化的时代。但严格的量化说起来容易做起来难。在生物学等复杂系统中，收集数据可能既困难又昂贵。在医学和金融等高风险应用中，考虑不确定性至关重要。变分推理——人工智能研究前沿的一种方法——是解决这些问题的一种方法。

   本教程向您介绍基础知识：变分推理的时间、原因和方式。

二、变分推理什么时候有用？

   变分推理在以下三个密切相关的用例中很有吸引力：

1. 如果您的数据很少（即观察次数较少），
2. 你关心不确定性，
3. 用于生成建模。

   我们将在我们的工作示例中讨论每个用例。

2.1. 少量数据的变分推理

图 1：变分推理允许您将领域知识与示例中的信息进行权衡。图片由作者提供。
   有时，数据收集的成本很高。例如，DNA 或 RNA 测量每次观察很容易花费数千欧元。在这种情况下，您可以对领域知识进行硬编码来代替额外的示例。当您收集更多示例并更加依赖数据时，变分推理可以帮助系统地“缩减”领域知识（图 1）。

2.2. 不确定性的变分推断

   对于金融和医疗保健等安全关键型应用，不确定性非常重要。不确定性会影响模型的各个方面，最明显的是预测输出。不太明显的是模型的参数（例如权重和偏差）。您可以赋予参数一个分布，使其变得模糊，而不是通常的数字数组（权重和偏差）。变分推理允许您推断合理值的范围。

2.3. 生成模型的变分推理

   生成模型提供了数据生成方式的完整规范。例如，如何生成猫或狗的图像。通常，存在一个带有语义含义的潜在表示z （例如， z描述一只暹罗猫）。通过一组（非线性）变换和采样步骤，z被变换为实际图像x（例如，暹罗猫的像素值）。变分推理是一种推断潜在语义空间z并从中采样的方法。一个众所周知的例子是变分自动编码器。

三、什么是变分推理？

   从本质上讲，变分推理是一项贝叶斯事业[1]。从贝叶斯的角度来看，你仍然让机器像往常一样从数据中学习。不同的是，您给模型一个提示（先验）并允许解决方案（后验）更加模糊。更具体地说，假设您有一个包含m 个示例的训练集X = [ x ₁, x 2,…, x ₘ ]ᵗ 。我们使用贝叶斯定理：

p ( θ | X ) = p ( X | θ ) p ( θ ) / p ( X ),

   推断解θ的范围（分布）。将此与传统的机器学习方法进行对比，在传统的机器学习方法中，我们最小化损失ℒ( θ, X ) = ln p ( X | θ ) 以找到一个特定的解决方案θ。 贝叶斯推理围绕着寻找一种方法来确定页（θ|X）： 这后部参数分布θ给定训练集X。总的来说，这是一个难题。实际中可以采用两种方法来求解页（θ|X): (i) 使用模拟 (马尔可夫链蒙特卡罗) 或 (ii) 通过优化。变分推理是关于选项（ii）的方法。

证据下限 (ELBO)

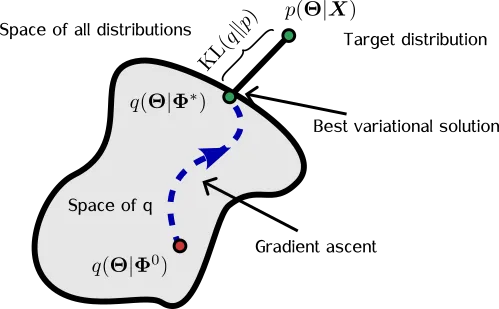
图 2：变分推理示意图。我们寻找接近 p(θ|X) 的分布 q(θ)。图片由作者提供。
   变分推理背后的想法是寻找一个分布q ( θ )，它是p ( θ | X )的替代（代理）。然后，我们尝试通过更改Φ的值来使q [ θ|Φ ( X )] 看起来与p ( θ | X ) 相似（图 2）。这是通过最大化证据下限 (ELBO) 来完成的：

$$\mathcal{L}（\Phi ）=E[lnp（X，\Theta ）—lnq（\Theta |\Phi ）]，$$

   其中期望 E[·] 取自q ( θ|Φ )。 （请注意，Φ隐式依赖于数据集X，但为了符号方便，我们将放弃显式依赖。）

   对于ℒ的基于梯度的优化，乍一看，我们在求导数（相对于Φ）时必须小心，因为 E[·] 依赖于q ( θ|Φ )。幸运的是，像JAX这样的 autograd 包支持重新参数化技巧 [2]，允许您直接从随机样本（例如伽玛分布）中获取导数，而不是依赖高方差黑盒变分方法 [3]。长话短说：用一批[ θ ₁, θ 2,…] ~ q ( θ|Φ ) 估计 ∇ℒ(Φ) ，让你的 autograd 包关心细节。

四、从头开始的变分推理

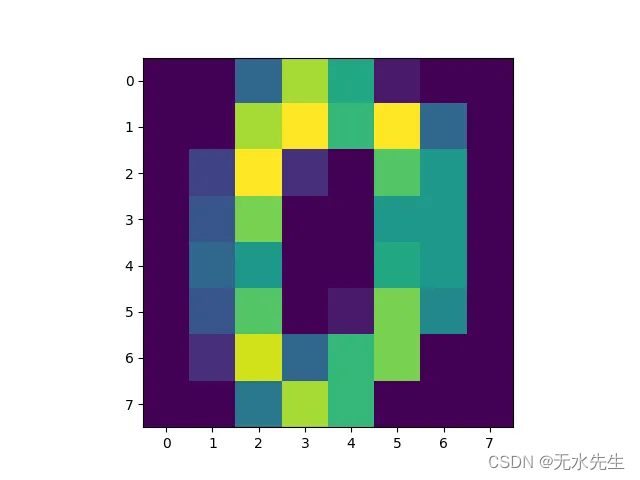
图 3：来自 sci-kit learn 数字数据集的手写“0”的示例图像。图片由作者提供。
   为了巩固我们的理解，让我们使用JAX从头开始​​实现变分推理。在此示例中，您将使用sci-kit learn中的手写数字训练生成模型。您可以按照Colab 笔记本进行操作。

   为了简单起见，我们只分析数字“零”。

from sklearn import datasetsdigits 

= datasets.load_digits() 
is_zero =digits.target == 0
 X_train =digits.images[is_zero] 
 # 将图像网格展平为向量。
 n_pixels = 64   # 8×8。
 X_train = X_train.reshape((- 1 , n_pixels))

   每个图像都是一个 8×8 的离散像素值数组，范围从 0 到 16。由于像素是计数数据，因此我们使用泊松分布对像素x进行建模，其中伽玛先验的速率为θ。速率θ确定像素的平均强度。因此，联合分布由下式给出：
$$p(x,\Theta )=Poisson(x|\Theta )Gamma(\Theta |a,b),$$

   其中a和b是伽马分布的形状和比率。

图 4：使用数字“零”的领域知识作为先验。图片由作者提供。
   先验 — 在本例中为 Gamma( θ | a , b ) — 是您注入领域知识的地方（用例 1.）。例如，您可能知道“平均”数字零是什么样的（图 4）。您可以使用此先验信息来指导您对a和b的选择。使用图 4 作为先验信息（我们称之为x ₀）并作为两个例子来衡量其重要性，然后设置a = 2 x ₀；b = 2。

用 Python 写出来是这样的：

import jax.numpy as jnp
import jax.scipy as jsp

# Hyperparameters of the model.
a = 2. * x_domain_knowledge
b = 2.

def log_joint(θ):
  log_likelihood = jnp.sum(jsp.stats.gamma.logpdf(θ, a, scale=1./b))
  log_likelihood += jnp.sum(jsp.stats.poisson.logpmf(X_train, θ))
  return log_likelihood

   请注意，我们使用了numpy 和 scipy 的JAX实现，以便我们可以求导数。

   接下来，我们需要选择一个代理分布q ( θ|Φ )。提醒您，我们的目标是更改Φ以使代理分布q ( θ|Φ ) 与p ( θ|X)匹配。因此， q ( θ )的选择决定了近似水平（在上下文允许的情况下，我们抑制对Φ的依赖）。出于说明目的，让我们选择一个由 gamma（的乘积）组成的变分分布：
$$q(\Theta |\Phi )=Gamma(\Theta |\alpha ,\beta ),$$

   其中我们使用简写形式Φ = { α , β }。

   接下来，要实现证据下界ℒ ( Φ ) = E[ln p ( X , θ ) — ln q ( θ|Φ )]，首先写下期望括号内的项：

@partial(vmap, in_axes=(0, None, None))
def evidence_lower_bound(θ_i, alpha, inv_beta):
  elbo = log_joint(θ_i) - jnp.sum(jsp.stats.gamma.logpdf(θ_i, alpha, scale=inv_beta))
  return elbo

   在这里，我们使用 JAX 的vmap对函数进行向量化，以便我们可以批量运行它[ θ ₁, θ 2,…, θ ₁ϋ₈]ᵗ。

   为了完成ℒ ( Φ )的实现，我们对上述函数在变分分布θ ᵢ ~ q ( θ ) 的实现上进行平均：

def loss(Φ: dict, key):
  """Stochastic estimate of evidence lower bound."""
  alpha = jnp.exp(Φ['log_alpha'])
  inv_beta = jnp.exp(-Φ['log_beta'])

  # Sample a batch from variational distribution q.
  batch_size = 128
  batch_shape = [batch_size, n_pixels]
  θ_samples = random.gamma(key, alpha , shape=batch_shape) * inv_beta
  
  # Compute Monte Carlo estimate of evidence lower bound.
  elbo_loss = jnp.mean(evidence_lower_bound(θ_samples, alpha, inv_beta))
  
  # Turn elbo into a loss.
  return -elbo_loss

   关于这些论点，有几点需要注意：

• 我们将Φ打包为包含 ln( α ) 和 ln( β )的字典（或者从技术上讲，是pytree ） 。这个技巧保证了优化过程中α > 0 且β > 0（伽玛分布提出的要求）。
• 损失是ELBO 的随机估计。在 JAX 中，每次采样时我们都需要一个新的伪随机数生成器 (PRNG)密钥。在这种情况下，我们使用key来采样[ θ ₁, θ 2,…, θ ₁ϋ₈]ᵗ。
  这就完成了模型p ( x , θ)、变分分布q ( θ ) 和损失ℒ ( Φ )的规范。

五、模型训练

   接下来，我们通过改变Φ = { α , β }来最小化损失ℒ ( Φ )，以使q ( θ|Φ ) 与后验p ( θ | X ) 匹配。如何？使用老式的梯度下降！为了方便起见，我们使用Optax的 Adam 优化器，并使用先验α = a和β = b初始化参数[记住，先验是Gamma( θ | a , b ) 并编码了我们的领域知识]。

# Initialise parameters using prior.
Φ = {
    'log_alpha': jnp.log(a),
    'log_beta': jnp.full(fill_value=jnp.log(b), shape=[n_pixels]),
}

loss_val_grad = jit(jax.value_and_grad(loss))
optimiser = optax.adam(learning_rate=0.2)
opt_state = optimiser.init(Φ)

   在这里，我们使用value_and_grad同时评估 ELBO 及其导数。方便监控收敛！然后，我们及时编译生成的函数（使用jit）以使其变得敏捷。

   最后，我们将模型训练 5000 步。由于损失是随机的，因此对于每次评估，我们需要为其提供伪随机数生成器（PRNG）密钥。我们通过使用random.split分配 5000 个键来实现这一点。

n_iter = 5_000
keys = random.split(random.PRNGKey(42), num=n_iter)

for i, key in enumerate(keys):
  elbo, grads = loss_val_grad(Φ, key)
  updates, opt_state = optimiser.update(grads, opt_state)
  Φ = optax.apply_updates(Φ, updates)

   恭喜！您已经使用变分推理成功训练了您的第一个模型！您可以在 Colab 上访问带有完整代码的笔记本。

六、结果

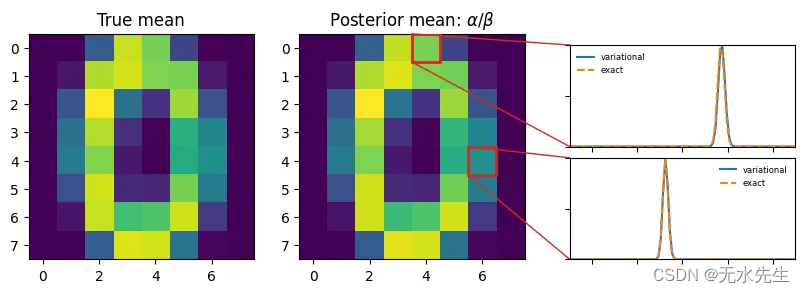
图 5：变分分布与精确后验分布的比较。图片由作者提供。
   让我们退后一步，欣赏我们所构建的内容（图 5）。对于每个像素，代理q ( θ ) 描述平均像素强度的不确定性（用例 2.）。特别是，我们选择的q ( θ ) 捕获了两个互补元素：

6.1 典型的像素强度。

图像与图像之间的强度差异有多大（变异性）。
事实证明，我们选择的联合分布p ( x , θ ) 有精确解：

$$p（\Theta |X）=Gamma（\Theta |a+\Sigma x_i，m+b），$$

   其中m是训练集X中的样本数量。在这里，我们清楚地看到，当我们收集更多示例x ᵢ时，在a和b中编码的领域知识是如何减少的。

   我们可以轻松地将学习到的形状α和速率β与真实值a + Σ x ᵢ 和m + b进行比较。在图 5 中，我们比较了两个特定像素的分布 — q ( θ|Φ ) 与p ( θ|X) 。你瞧，完美的搭配！

6,2 生成合成图像

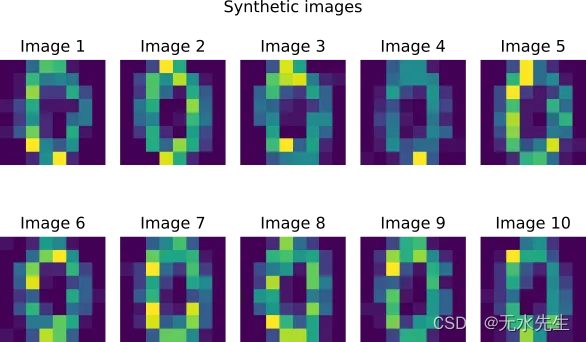
图 6：使用变分推理合成生成的图像。图片由作者提供。
   变分推理非常适合生成建模（用例 3）。有了备用后验q ( θ )，生成新的合成图像就变得微不足道了。这两个步骤是：

• 样本像素强度θ ~ q ( θ )。

# Extract parameters of q.
alpha = jnp.exp(Φ['log_alpha'])
inv_beta = jnp.exp(-Φ['log_beta'])

# 1) Generate pixel-level intensities for 10 images.
key_θ, key_x = random.split(key)
m_new_images = 10
new_batch_shape = [m_new_images, n_pixels]
θ_samples = random.gamma(key_θ, alpha , shape=new_batch_shape) * inv_beta

• 提取q的参数。

# 2) Sample image from intensities.
X_synthetic = random.poisson(key_x, θ_samples)

   您可以在图 6 中看到结果。请注意，“零”字符的锐度略低于预期。这是我们建模假设的一部分：我们将像素建模为相互独立而不是相关。为了考虑像素相关性，您可以将模型扩展为聚类像素强度：这称为泊松分解 [4]。

七、总结

   在本教程中，我们介绍了变分推理的基础知识，并将其应用于一个玩具示例：学习手写数字零。借助 autograd，从头开始实现变分推理只需几行 Python 代码。

   如果数据很少，变分推理就特别强大。我们了解了如何将领域知识与数据信息进行融合和交换。推断的代理分布q ( θ ) 给出模型参数的“模糊”表示，而不是固定值。如果您处于不确定性很重要的高风险应用中，那么这是理想的选择！最后，我们演示了生成建模。一旦可以从q ( θ ) 采样，生成合成样本就很容易。

   总之，通过利用变分推理的力量，我们可以解决复杂的问题，使我们能够做出明智的决策，量化不确定性，并最终释放数据科学的真正潜力。