cspccf备考

13年12月CCF计算机软件能力认证

3192. 出现次数最多的数

给定$n$个正整数，找出它们中出现次数最多的数。
如果这样的数有多个，请输出其中最小的一个。

输入格式

输入的第一行只有一个正整数$n$,表示数字的个数。
输入的第二行有$n$个整数$s_1,s_2,\dots ,s_n$ 。
相邻的数用空格分隔。

输出格式

输出这$n$个次数中出现次数最多的数。
如果这样的数有多个，输出其中最小的一个。

数据范围

$$\begin{array}{rl}& 1\le n\le 1000,\\ & 1\le s_i\le 10000\end{array}$$

输入样例：

6
10110203020

输出样例：

10

}

数组模拟

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int c[N];
int n;
int mx = 1e5 + 10, cnt;

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n;
    while (n -- )
    {
        int x;
        cin >> x;
        c[x] ++;
        if(c[x] > cnt)
        {
            cnt = c[x];
            mx = x;
        }
        if(c[x] == cnt && x < mx)
            mx = x;
    }
    cout << mx << endl;
    return 0;
}

Map

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int mx = N, cnt;
int n;
map<int, int> mp;

int main()
{
    cin >> n;
    while (n -- )
    {
        int x;
        cin >> x;
        mp[x] ++;
        if(mp[x] > cnt)
        {
            cnt = mp[x];
            mx = x;
        }
        if(mp[x] == cnt && x < mx)
            mx = x;
    }
    cout << mx << endl;
    return 0;
}

3193. ISBN号码

每一本正式出版的图书都有一个 ISBN 号码与之对应。
ISBN 码包括9位数字、1位识别码和3位分隔符，其规定格式如 x-xxx-xxxxx-x ,其中符号 - 是分隔符 (键盘上的减号),最后一位是识别码，例如 0-670-82162-4 就是一个标准的ISBN码。
ISBN 码的首位数字表示书籍的出版语言，例如0代表英语；第一个分隔符 - 之后的三位数字代表出版社，例如670代表维京出版社；第二个分隔之后的五位数字代表该书在出版社的编号；最后一位为识别码。
识别码的计算方法如下：
首位数字乘以1加上次位数字乘以2…以此类推，用所得的结果mod 11,所得的余数即为识别码，如果余数为 10,则识别码为大写字母$X.$
例如ISBN 号码 0-670-82162-4 中的识别码4是这样得到的：对067082162这 9 个数字，从左至右，分别乘以
$1,2,\dots ,9$,再求和，即$0\times 1+6\times 2+\dots \dots +2\times 9=158$,然后取158 mod 11的结果 4 作为识别码。
编写程序判断输入的 ISBN 号码中识别码是否正确，如果正确，则仅输出 Right;如果错误，则输出是正确的ISBN 号码。
输入格式
输入只有一行，是一个字符序列，表示一本书的 ISBN 号码 (保证输入符合 ISBN 号码的格式要求)。
输出格式
输出一行，假如输入的ISBN 号码的识别码正确，那么输出 Right,否则，按照规定的格式，输出正确的 ISBN号码(包括分隔符 -)。
输入样例1：

0-670-82162-4

输出样例1：

Right

输入样例2：

0-670-82162-0

输出样例2：

0-670-82162-4

#include <bits/stdc++.h>
using namespace std;

int main()
{
    string s;
    cin >> s;
    for(int i = 0; i < s.size(); i ++)
        if(s[i] == '-')
            s.erase(i, 1);

    int res = 0;
    for(int i = 0; i < s.size() - 1; i ++)
        res += (s[i] - '0') * (i + 1);
    
    int m = res % 11;
    if(m == s[s.size() - 1] - '0')
        cout << "Right" << endl;
    else if(m == 10 && s[s.size() - 1] == 'X')
        cout << "Right" << endl;
    else
    {
        for(int i = 0; i < s.size() - 1; i ++)
        {
            cout << s[i];
            if(i == 0 || i == 3 || i == 8)
                cout << '-';
        }
        if(m == 10)
            cout << 'X';
        else
            cout << m;            
    }
    return 0;
}

3194. 最大的矩形

在横轴上放了$n$个相邻的矩形，每个矩形的宽度是1，而第$i$ ($1\le i\le n$)个矩形的高度是$h_i$。
这$n$个矩形构成了一个直方图。
例如，下图中六个矩形的高度就分别是3，1,6,5,2,3.

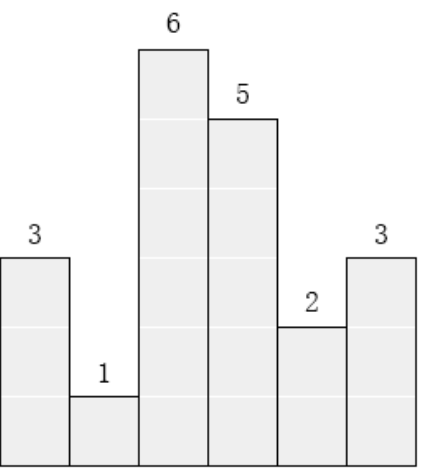
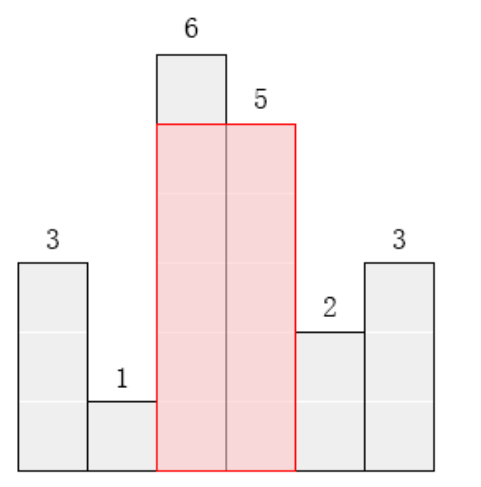
请找出能放在给定直方图里面积最大的矩形，它的边要与坐标轴平行。对于上面给出的例子，最大矩形如下图所示的阴影部分，面积是10。

输入格式

第一行包含一个整数$n$,即矩形的数量。
第二行包含$n$个整数$h_1,h_2,\dots ,h_n$ ,相邻的数之间由空格分隔。$h_i$是第$i$个矩形的高度。
输出格式
输出一行，包含一个整数，即给定直方图内的最大矩形的面积。

数据范围

$1\le n\le 1000$, $1\le h_i\le 10000$ 经实测$h_i$在官网的实际范围是$1\le h_i\le 40000$,这与其给出的题面描述不符，属于官网出题人的失误，也因此卡住了一些同学的代码，望大家加以注意。

输入样例：

6
3 1 6 5 2 3

输出样例：

10

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int h[N];
int n;
int res;

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++)
        cin >> h[i];
    
    for(int i = 1; i <= n; i ++)
    {
        int l, r;
        for(int j = i; j >=1; j --)
        {
            if(h[i] > h[j]) break;
            l = j;
        }
        for(int j = i; j <= n; j ++)
        {
            if(h[i] > h[j]) break;
            r = j;
        }
        res = max(res, h[i] * (r - l + 1));
    }
    cout << res << endl;
    return 0;
}