1. 什么是树状数组
最近也是在学左神视频里面树状数组相关的,也包括 b 站上面一些树状数组的视频,所以也顺便做下笔记,视频:算法讲解108【扩展】树状数组原理、扩展、代码详解。
首先就是树状数组解决了什么问题,对于前缀和我们就知道可以用来解决范围查询问题,而如果是差分就可以用来解决 k 次范围修改之后这个数组会变成什么样这类的问题。现在有一个问题,给你一个数组 arr,有 k 次操作,每一次操作有两种情况:
- 对这个数组的某个下标 +v,也就是 add(arr,index,v)
- 求出这个数组 [L,R] 范围的总和,也就是 sum(arr,L,R)
也就是说我们需要一边维护数组,一遍输出范围求和,那输出范围总和简单来说可以用前缀和以 O(1) 的时间完成,但是如果要加上 +v 就有问题了,如果我们是维护前缀和,就需要对下标 arr[index ] +v 的同时,对 index 后面的下标也要统一 + v,比如数组 [1,2,3,4,5],前缀和是[1,3,6,10,15],如果有一个操作要对 arr[2] + 4,那么同样的我们在维护的时候需要将 arr[3] + 4,arr[4] + 4,因为前缀和某个下标 +v 会影响到后面的所有下标,所以最终的结果就是 [1,3,10,14,19],那么这种情况下我们求比如 [2,4] 的前缀和就可以直接通过数组算出来是 19 - 3 = 16,但是整个过程在 add 的时候时间复杂度是 O(n) 的。
而树状数组就可以去解决这个问题,尤其是这种单点增加,范围查询问题,但是也不止这一类:
- 单点增加,范围查询
- 范围增加,单点查询
- 范围增加,范围查询
2. 树状数组的结构与代码

首先来看下这样的一个结构,最底层是我们的数组 arr,长度是 8,假设现在对 arr[3] + 4,我们要快速维护整个结构,需要将 涉及到 arr[3] 这个下标的位置都 + 4,就变成了下面的图。

这样假设我们要快速求下标 [2,5] 这个范围的累加和,就很简单了,可以直接将两个方框的值加起来,就是范围的累加和了。

但是这样有一个问题,就是我们如果要保存这个结构,需要的空间是比较大的,所以就看下能不能删掉一些没有必要的格子,观察上面我们发现有一些格子删掉之后完全不影响计算。

比如删掉这些格子之后,我们会得到上面的结构,这个结构里面,我们可以随便求出 [0,x] 这个范围的累加和,比如 [0,0] 就是上面的蓝色集合,[0,2] 就是上面的绿色格子,[0,5] 就是上面的红色格子加起来,那么既然能随意求出 [0,x] 这个范围的累加和,对于任意的 [L,R] 范围的累加和也能求出来了,只需要求出 [0,R] 的累加和,减去 [0,L - 1] 的累加和就行了。
而且为了让上面的结构更直观,我们将上面的格子给连接起来,同时对于上面的每一个格子,用一个数组 tree 存起来,下标从 1 开始,这个 tree 数组就是树状数组,注意树状数组需要从 1 开始。

可以看到上面就是树状数组的结构,而且数组数组有这样的规律:
- tree[1] 是原数组 arr[1] 的值
- tree[2] 是原数组 arr[1] + arr[2] 的值
- tree[3] 是原数组 arr[3] 的值
- tree[4] 是原数组 arr[1] + arr[2] + arr[3] + arr[4] 的值
- …
可以发现上面图中每个下标的值就是覆盖的下标范围的总和,所以假设现在我们要在原数组的 arr[1] + 4,那也就是说 tree[1] + 4,这时候 tree[2] 也要 + 4,tree[4] 也要 + 4,tree[8] 也要 + 4,相当于说子节点 + v,我们要找到遍历子节点的父结点同时都 + v。
那么如何找到下标的父结点呢,首先引入一个知识 lowbit,lowbit 可以求出一个数最右边的 1,比如 5 = 101,那么 lowbit(5) = 1,6 = 110,那么 lowbit(6) = 2,我们可以看下树状数组中每一个下标的 lowbit 值。
public static int lowbit(int i) {
return i & -i;
}

可以发现处于同一层的节点的 lowbit 值是相等的,而且我们要找到一个下标的父结点,可以通过 i + lowbit(i) 完成,比如上面我们要找到 5 的父结点就是 5 + lowbit(5) = 6,要找到 6 的父结点可以通过 6 + lowbit(6) = 8 来完成,因此当我们给一个下标 + v 的时候可以通过下面的代码来完成树状数组的维护。
// 给树状数组的下标 i + v
public static void add(int i, int v) {
while (i <= n) {
tree[i] += v;
i += lowbit(i);
}
}
然后再来看下如何求出 1~index 这个范围的总和,比如下面我要求 [1,index] 这个范围的区间总和,那么就可以从 index 开始,不断减去 lowbit(index),就是这个范围的总和了,比如我们要求 [1,7] 这个范围的区间总和,就可以用 tree[7] + tree[6] + tree[4] 算出来,而我们可以发现 7 - lowbit(7) = 6,6 - lowbit(6) = 4。
public static int sum(int i) {
int ans = 0;
while (i > 0) {
ans += tree[i];
i -= lowbit(i);
}
return ans;
}
可以看,下面图中红色部分就是求和,这个方法对于 [1,index] 范围的求和都是适用的。

3. 树状数组单点增加,范围查询模板
P3374 【模板】树状数组 1,树状数组,属于单点增加,范围查询的题目,下面就是模板,注意下面下标是从 1 开始,因为上面的结构,包括 sum、range、add 函数,都是需要从下标 1 开始算的。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
public class Main {
public static int[] tree = null;
public static int n, m;
public static int lowbit(int i) {
return i & -i;
}
public static void add(int i, int v) {
while (i <= n) {
tree[i] += v;
i += lowbit(i);
}
}
public static int sum(int i) {
int ans = 0;
while (i > 0) {
ans += tree[i];
i -= lowbit(i);
}
return ans;
}
public static int range(int l, int r) {
return sum(r) - sum(l - 1);
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
in.nextToken();
n = (int) in.nval;
in.nextToken();
m = (int) in.nval;
tree = new int[n + 1];
for (int i = 1, v; i <= n; i++) {
in.nextToken();
v = (int) in.nval;
add(i, v);
}
for (int i = 1; i <= m; i++) {
in.nextToken();
int type = (int) in.nval;
if (type == 1) {
in.nextToken();
int index = (int) in.nval;
in.nextToken();
int v = (int) in.nval;
add(index, v);
} else {
in.nextToken();
int l = (int) in.nval;
in.nextToken();
int r = (int) in.nval;
out.println(range(l, r));
}
}
out.flush();
out.close();
br.close();
}
}
4. 树状数组如何范围增加,单点查询
树状数组除了可以单点增加,单点查询,还可以用来范围增加,单点查询。如果想要用于范围增加,就需要从差分数组入手,之前二维数组和一维数组中我们也说过差分数组,比如对于数组 [1,2,3,4,5],差分数组就是 [1,1,1,1,1],差分数组的妙处就是使用前缀和之后就能求出原始数组,而且对于原数组的范围 [L,R] + v,我们只需要对差分数组 d[L] + v,d[R + 1] - v 即可。
换成树状数组也是一样的,我们使用树状数组维护原数组的差分信息,最后单点查询的时候使用 sum 方法,就相当于求前缀和,举个例子,比如原数组是 [1,2,3,4,5,6,7,8],那么差分数组就是 [1,1,1,1,1,1,1,1],树状数组维护的就是差分数组信息。
构造差分数组有两种方式,一种是先读取原数组,然后再根据原数组构造差分数组。另一种是我们可以边读取原数组的下标值,边构造差分数组,这样比较方便,比如原数组是 [1,2,3,4,5,6,7,8],我们可以先假设原数组是 [0,0,0,0,0,0,0,0],然后做 8 次操作,分别是:[0,0] + 1,[1,1] + 2 … [8,8] + 8,经过这 8 次操作之后原数组就会变成 [1,2,3,4,5,6,7,8],那么对应的差分数组 tree 的维护就如下图所示。

假设现在要在原数组做3个操作:
- 对数组 [2,4] 范围内的数字 + 4
- 对数组 [3,7] 范围内的数字 + 3
- 对数组 [1,5] 范围内的数字 - 2
我们先来看下原数组 [1,2,3,4,5,6,7,8] 经过这几个步骤之后变成了什么。

那么对于树状数组,就需要执行下面 6 个步骤。
- tree[2] + 4,tree[5] - 4
- tree[3] + 3,tree[8] - 3
- tree[1] - 2,tree[6] + 2
结果如下:
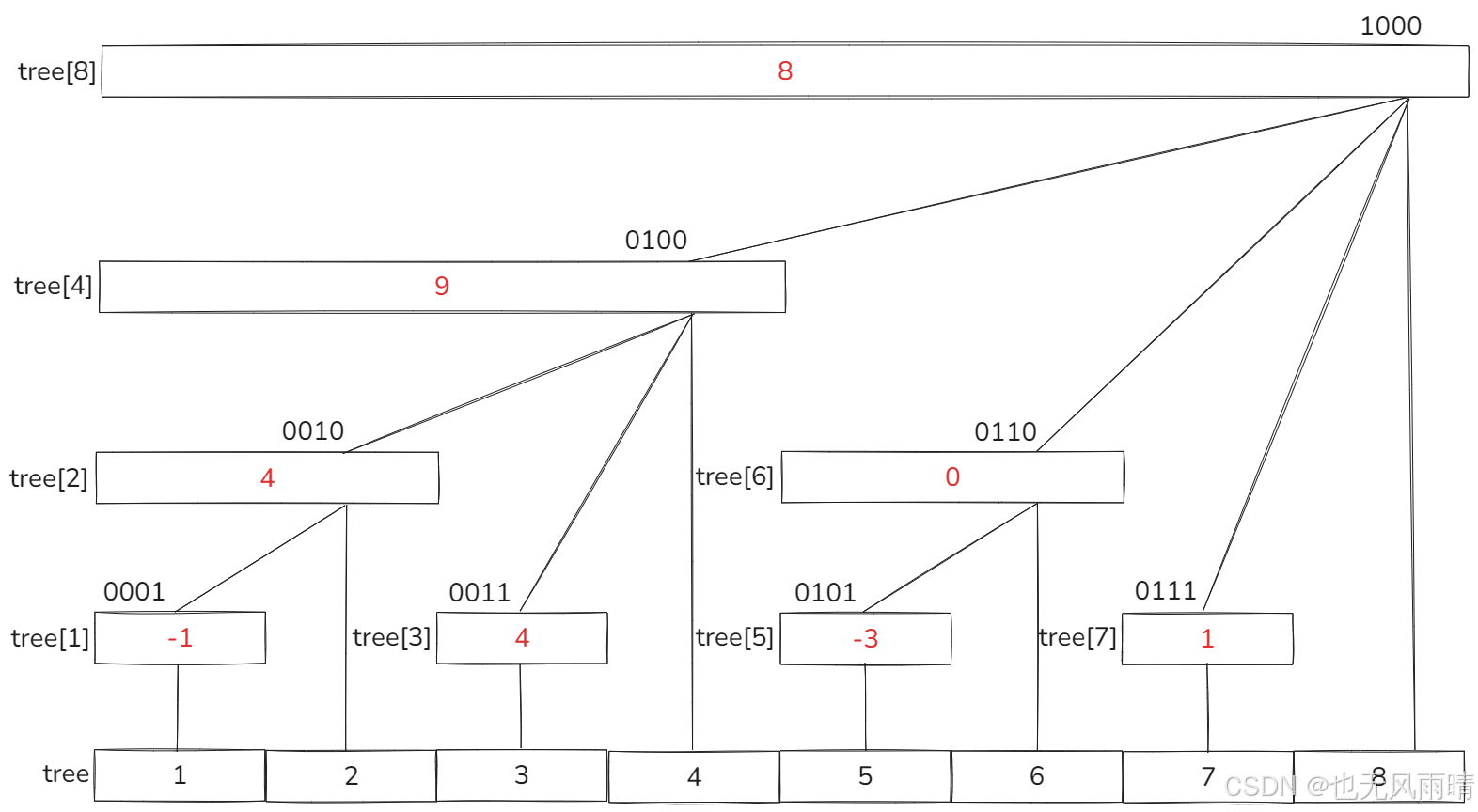
接下来可以通过 tree 求出原数组修改后的每一个下标的值:
- arr[1] = sum(1) = tree[1] = -1
- arr[2] = sum(2) = tree[2] = 4
- arr[3] = sum(3) = tree[3] + tree[2] = 8
- arr[4] = sum(4) = tree[4] = 9
- arr[5] = sum(5) = tree[5] + tree[4] = -3 + 9 = 6
- arr[6] = sum(6) = tree[6] + tree[4] = 9 + 0 = 9
- arr[7] = sum(7) = tree[7] + tree[6] + tree[4] = 10
- arr[8] = sum(8) = tree[8] = 8
可以看到通过树状数组算出来的值跟我们上面手动算出来的是一样的,那么下面就来看下代码。
5. 树状数组范围增加,单点查询模板
还是一样,看题目 P3368 【模板】树状数组 2。
import java.io.*;
import java.util.*;
import java.lang.*;
public class Main {
static int n = 0, m = 0;
static int[] tree = null;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
in.nextToken();
n = (int) in.nval;
tree = new int[n + 1];
in.nextToken();
m = (int) in.nval;
for (int i = 1; i <= n; i++) {
in.nextToken();
int v = (int) in.nval;
// 维护数组的差分信息
add(i, v);
add(i + 1, -v);
}
for (int i = 1; i <= m; i++) {
in.nextToken();
int type = (int) in.nval;
if (type == 1) {
in.nextToken();
int l = (int) in.nval;
in.nextToken();
int r = (int) in.nval;
in.nextToken();
int v = (int) in.nval;
add(l, v);
add(r + 1, -v);
} else {
in.nextToken();
int index = (int) in.nval;
out.println(sum(index));
}
}
out.flush();
out.close();
br.close();
}
public static int sum(int index) {
int sum = 0;
while(index > 0){
sum += tree[index];
index -= lowbit(index);
}
return sum;
}
public static void add(int i, int num) {
while (i <= n) {
tree[i] += num;
i += lowbit(i);
}
}
public static int lowbit(int i) {
return i & -i;
}
}
6. 树状数组范围增加、范围查询模板
范围增加和查询用线段树来做好点,但是树状数组也能写,首先还是一样,既然要范围增加,就需要维护差分数组,假设差分数组是 d,原数组 arr,现在有下面的公式。
- a r r [ 1 ] = d [ 1 ] arr[1] = d[1] arr[1]=d[1]
- a r r [ 2 ] = d [ 1 ] + d [ 2 ] arr[2] = d[1] + d[2] arr[2]=d[1]+d[2]
- a r r [ k ] = d [ 1 ] + d [ 2 ] + . . . + d [ k ] arr[k] = d[1] + d[2]+ ... + d[k] arr[k]=d[1]+d[2]+...+d[k]
然后如果我们要求 [L,R] 这个范围的下标总和,那么只需要用 sum® - sum(L - 1),所以这里的关键就是如何定义 sum 函数,也就是如何求出 [1…k] 这个范围的总和。
从上面的公式也可以看到:
- a r r [ 1 ] + a r r [ 2 ] + . . . + a r r [ k ] = d [ 1 ] + ( d [ 1 ] + d [ 2 ] ) + . . . + ( d [ 1 ] + d [ 2 ] + . . . + d [ k ] ) arr[1] + arr[2] + ... + arr[k] = d[1] + (d[1] + d[2]) + ... + (d[1] + d[2] + ... + d[k]) arr[1]+arr[2]+...+arr[k]=d[1]+(d[1]+d[2])+...+(d[1]+d[2]+...+d[k])
对右边的式子简化,得到下面的式子:
- k ∗ d [ 1 ] + ( k − 1 ) ∗ d [ 2 ] + . . . + ( k − ( k − 1 ) ) ∗ d [ k ] k * d[1] + (k-1) * d[2] + ... + (k - (k-1)) * d[k] k∗d[1]+(k−1)∗d[2]+...+(k−(k−1))∗d[k]
我们把 i 提取出来,得到下面的式子:
- k ∗ ( d [ 1 ] + d [ 2 ] + . . . + d [ k ] ) − ( d [ 2 ] + 2 ∗ d [ 3 ] + . . . + ( k − 1 ) ∗ d [ k ] ) k * (d[1] + d[2] + ... + d[k]) - (d[2] + 2 * d[3] + ... + (k-1)* d[k]) k∗(d[1]+d[2]+...+d[k])−(d[2]+2∗d[3]+...+(k−1)∗d[k])
最后化简得到:
- k ∗ ∑ i = 1 k d i − ∑ i = 1 k ( i − 1 ) ∗ d i k * \sum_{i=1}^{k}d_{i} - \sum_{i=1}^{k} (i-1) * d_{i} k∗∑i=1kdi−∑i=1k(i−1)∗di
所以我们代码中主要就是维护两个差分数组,一个是 d,一个是 (i - 1) * d,我们用数组 tree1 和 tree2 维护这两个差分数组,接着对于 [L,R] 范围内的累加和就可以这么写。
public static long range(int l, int r) {
return sum(tree1, r) * r - sum(tree2, r)
- sum(tree1, l - 1) * (l - 1) + sum(tree2, l - 1);
}
然后如果要维护树状数组,add 函数可以这么写。
public static void add(int l, int r, int v){
add(tree1, l, v);
add(tree1, r + 1, -v);
// (l - 1) * v
add(tree2, l, (l - 1) * v);
// -(r + 1 - 1) * v
add(tree2, r + 1, -(r * v));
}
public static void add(long[] tree, int i, long v) {
while (i <= n) {
tree[i] += v;
i += lowbit(i);
}
}
下面就来看这道题,是线段树的题目,但是可以用树状数组来写,P3372 【模板】线段树 1。

import java.io.*;
import java.util.*;
import java.lang.*;
public class Main {
static int n = 0, m = 0;
// 原始差分信息 Di
static long[] tree1 = null;
// 差分公式第二段的 (i - 1) * Di
static long[] tree2 = null;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
in.nextToken();
n = (int) in.nval;
tree1 = new long[n + 1];
tree2 = new long[n + 1];
in.nextToken();
m = (int) in.nval;
for (int i = 1; i <= n; i++) {
in.nextToken();
long v = (long) in.nval;
// 维护数组的差分信息
add(i, i, v);
}
for (int i = 1; i <= m; i++) {
in.nextToken();
int type = (int) in.nval;
if (type == 1) {
in.nextToken();
int l = (int) in.nval;
in.nextToken();
int r = (int) in.nval;
in.nextToken();
long v = (long) in.nval;
add(l, r, v);
} else {
in.nextToken();
int l = (int) in.nval;
in.nextToken();
int r = (int) in.nval;
out.println(sum(l, r));
}
}
out.flush();
out.close();
br.close();
}
public static long sum(int l, int r){
return sum(tree1, r) * r - sum(tree2, r) - sum(tree1, l - 1) * (l - 1) + sum(tree2, l - 1);
}
public static void add(int l, int r, long v){
add(tree1, l, v);
add(tree1, r + 1, -v);
add(tree2, l, (l - 1) * v);
add(tree2, r + 1, - (r * v));
}
public static long sum(long[] tree, int index) {
long sum = 0;
while(index > 0){
sum += tree[index];
index -= lowbit(index);
}
return sum;
}
public static void add(long[] tree, int i, long num) {
while (i <= n) {
tree[i] += num;
i += lowbit(i);
}
}
public static int lowbit(int i) {
return i & -i;
}
}
7. 二维树状数组单点增加、范围查询
二维树状数组和一维的是一样的,只是增加了一个维度,同样的也需要从下标 1 开始计算,由于视频里面的 leetcode 需要 vip … 所以直接就把视频的代码贴出来,二维数组求一个范围的累加和其实就是二维前缀和的代码。
class NumMatrix {
public int[][] tree;
public int[][] nums;
public int n;
public int m;
// 入参二维数组下标从0开始
// 树状数组一定下标从1开始
public NumMatrix(int[][] matrix) {
n = matrix.length;
m = matrix[0].length;
tree = new int[n + 1][m + 1];
nums = new int[n + 1][m + 1];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
update(i, j, matrix[i][j]);
}
}
}
private int lowbit(int i) {
return i & -i;
}
private void add(int x, int y, int v) {
for (int i = x; i <= n; i += lowbit(i)) {
for (int j = y; j <= m; j += lowbit(j)) {
tree[i][j] += v;
}
}
}
private int sum(int x, int y) {
int ans = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
for (int j = y; j > 0; j -= lowbit(j)) {
ans += tree[i][j];
}
}
return ans;
}
public void update(int x, int y, int v) {
add(x + 1, y + 1, v - nums[x + 1][y + 1]);
nums[x + 1][y + 1] = v;
}
public int sumRegion(int a, int b, int c, int d) {
return sum(c + 1, d + 1) - sum(a, d + 1) - sum(c + 1, b) + sum(a, b);
}
}
8. 二维数组范围增加,范围查询
上面是单点增加,范围查询的代码,这里是范围增加,范围查询的代码,其实有了范围增加,范围查询的代码,单点增加也可以用这个模板来写,下面来推导下,首先明确二维差分数组和原始数组的关系。

对于原始数组 arr 的值,我们可以用这个公式来通过差分数组 D 表示出来:
- a r r [ i ] [ j ] = ∑ x = 1 i ∑ y = 1 j D [ x ] [ y ] arr[i][j] = \sum_{x=1}^{i} \sum_{y=1}^{j} D[x][y] arr[i][j]=∑x=1i∑y=1jD[x][y]
注意这个公式我们是从下标 1 开始,因为树状数组需要从下标 1 开始才能有上面我们说的那些特性。
同时对于原始数组,如果要修改一个范围的值假设是 [1,1] 到 [2,2] + v,那么我们也只需要对差分数组做 4 个步骤:
- D[1][1] + v
- D[3][1] - v
- D[1][3] - v
- D[3][3] + v
换句话说,如果要对 [a,b] 到 [c,d] + v,那么对于差分数组 D,只需要修改四个步骤:
- D[a][b] + v
- D[c+1][b] - v
- D[a][d+1] - v
- D[c+1][d+1] + v
那我们就来看下如果要求原始数组的一个范围的累加和用差分数组怎么表达,首先明确原始数组某一个位置的值表达如下:
- a r r [ i ] [ j ] = ∑ x = 1 i ∑ y = 1 j D [ x ] [ y ] arr[i][j] = \sum_{x=1}^{i} \sum_{y=1}^{j} D[x][y] arr[i][j]=∑x=1i∑y=1jD[x][y]
那么如果现在我们要求一个范围的总和,怎么求呢?

所以最核心的方法是如何实现 sum(n,m) 这个方法,下面再通过上面的 arr[i][j] 来表达这个方法。
那首先 sum(n,m) 表示的是从右上角起点(1,1)到右下角(n,m)的累加和,可以写如下式子:
- s u m ( n , m ) = ∑ i = 1 n ∑ j = 1 m a r r [ i ] [ j ] = ∑ i = 1 n ∑ j = 1 m ∑ x = 1 i ∑ y = 1 j D [ x ] [ y ] sum(n, m) = \sum_{i=1}^{n} \sum_{j=1}^{m} arr[i][j] = \sum_{i=1}^{n} \sum_{j=1}^{m} \sum_{x=1}^{i} \sum_{y=1}^{j} D[x][y] sum(n,m)=∑i=1n∑j=1marr[i][j]=∑i=1n∑j=1m∑x=1i∑y=1jD[x][y]
但是这样看起来这个式子就有点复杂了,所以我们想办法把里面的 x 和 y 去掉,为什么是 x 和 y 呢,因为最终目的是求出 sum 方法,这个方法的传入参数是 n 和 m,跟 x 和 y 是无关的。所以我们下面就来看下里面的 x 和 y 如何去掉。

因为 x 的上限是 i,y 的上限是 j,所以求和的时候假设 i < 2 或者 j < 2,上面 D[2][2] 就不会出现,所以当 i >= 2 且 j >= 2 的时候 D[2][2] 才会出现,且整个四层嵌套调用下来 D[2][2] 出现的次数就是绿色的部分,所以我们直接遍历每一个下标,然后直接求这个格子最终出现的次数就行,写法如下:
- ∑ i = 1 n ∑ j = 1 m ∑ x = 1 i ∑ y = 1 j D [ x ] [ y ] = ∑ i = 1 n ∑ j = 1 m D [ i ] [ j ] ∗ ( n − i + 1 ) ∗ ( m − i + 1 ) \sum_{i=1}^{n} \sum_{j=1}^{m} \sum_{x=1}^{i} \sum_{y=1}^{j} D[x][y] = \sum_{i=1}^{n} \sum_{j=1}^{m} D[i][j] * (n - i + 1) * (m - i + 1) ∑i=1n∑j=1m∑x=1i∑y=1jD[x][y]=∑i=1n∑j=1mD[i][j]∗(n−i+1)∗(m−i+1)
然后化简得到:
- ( m + 1 ) ∗ ( n + 1 ) ∑ i = 1 n ∑ j = 1 m D [ i ] [ j ] − ( m + 1 ) ∗ ∑ i = 1 n ∑ j = 1 m ( i ∗ D [ i ] [ j ] ) − ( n + 1 ) ∗ ∑ i = 1 n ∑ j = 1 m ( j ∗ D [ i ] [ j ] ) + ∑ i = 1 n ∑ j = 1 m ( D [ i ] [ j ] ∗ i ∗ j ) (m + 1) * (n + 1) \sum_{i=1}^{n} \sum_{j=1}^{m} D[i][j]-(m + 1) * \sum_{i=1}^{n} \sum_{j=1}^{m} (i * D[i][j] ) - (n + 1) * \sum_{i=1}^{n} \sum_{j=1}^{m} (j * D[i][j] ) + \sum_{i=1}^{n} \sum_{j=1}^{m}(D[i][j] * i * j) (m+1)∗(n+1)∑i=1n∑j=1mD[i][j]−(m+1)∗∑i=1n∑j=1m(i∗D[i][j])−(n+1)∗∑i=1n∑j=1m(j∗D[i][j])+∑i=1n∑j=1m(D[i][j]∗i∗j)
所以一共需要维护四个差分信息:
- D [ i ] [ j ] D[i][j] D[i][j]
- D [ i ] [ j ] ∗ i D[i][j] * i D[i][j]∗i
- D [ i ] [ j ] ∗ j D[i][j] * j D[i][j]∗j
- D [ i ] [ j ] ∗ i ∗ j D[i][j] * i * j D[i][j]∗i∗j
代码里面的 add 方法如下:
// add 的时候维护四个差分数组的信息
public static void add(int x, int y, int v) {
int v1 = v;
int v2 = v * x;
int v3 = v * y;
int v4 = v * x * y;
for (int i = x; i <= n; i += lowbit(i)) {
for (int j = y; j <= m; j += lowbit(j)) {
tree1[i][j] += v1;
tree2[i][j] += v2;
tree3[i][j] += v3;
tree4[i][j] += v4;
}
}
}
求和就是上面的公式:
// 求 (1, 1) 到 (x, y) 的总和
public static int sum(int x, int y) {
int ans = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
for (int j = y; j > 0; j -= lowbit(j)) {
ans += (x + 1) * (y + 1) * tree1[i][j] - (y + 1) * tree2[i][j] - (x + 1) * tree3[i][j] + tree4[i][j];
}
}
return ans;
}
那下面看下代码和一道例题:P4514 上帝造题的七分钟。
import java.io.*;
import java.util.*;
import java.lang.*;
public class Main {
static int n = 0, m = 0;
// 差分信息: d[i][j]
public static int[][] tree1 = null;
// 差分信息: d[i][j] * i
public static int[][] tree2 = null;
// 差分信息: d[i][j] * j
public static int[][] tree3 = null;
// 差分信息: d[i][j] * j * i
public static int[][] tree4 = null;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
String op = "";
while (in.nextToken() != StreamTokenizer.TT_EOF) {
op = in.sval;
if (op.equals("X")) {
in.nextToken();
n = (int) in.nval;
in.nextToken();
m = (int) in.nval;
tree1 = new int[n + 1][m + 1];
tree2 = new int[n + 1][m + 1];
tree3 = new int[n + 1][m + 1];
tree4 = new int[n + 1][m + 1];
} else if (op.equals("L")) {
in.nextToken();
int a = (int) in.nval;
in.nextToken();
int b = (int) in.nval;
in.nextToken();
int c = (int) in.nval;
in.nextToken();
int d = (int) in.nval;
in.nextToken();
int v = (int) in.nval;
add(a, b, c, d, v);
} else {
in.nextToken();
int a = (int) in.nval;
in.nextToken();
int b = (int) in.nval;
in.nextToken();
int c = (int) in.nval;
in.nextToken();
int d = (int) in.nval;
System.out.println(sum(a, b, c, d));;
}
}
br.close();
}
// arr[a][b] 到 arr[c][d] 这个范围的下标都 + v
public static void add(int a, int b, int c, int d, int v) {
// 差分数组修改的四个操作
add(a, b, v);
add(a, d + 1, -v);
add(c + 1, b, -v);
add(c + 1, d + 1, v);
}
// add 的时候维护四个差分数组的信息
public static void add(int x, int y, int v) {
int v1 = v;
int v2 = v * x;
int v3 = v * y;
int v4 = v * x * y;
for (int i = x; i <= n; i += lowbit(i)) {
for (int j = y; j <= m; j += lowbit(j)) {
tree1[i][j] += v1;
tree2[i][j] += v2;
tree3[i][j] += v3;
tree4[i][j] += v4;
}
}
}
public static int lowbit(int i) {
return i & -i;
}
// 求 (1, 1) 到 (x, y) 的总和
public static int sum(int x, int y) {
int ans = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
for (int j = y; j > 0; j -= lowbit(j)) {
ans += (x + 1) * (y + 1) * tree1[i][j] - (y + 1) * tree2[i][j] - (x + 1) * tree3[i][j] + tree4[i][j];
}
}
return ans;
}
// 题目就是从 1 开始, 因此初始化的时候就会创建数组大小为 n + 1, m + 1, 所以这里不需要考虑边界
public static int sum(int a, int b, int c, int d) {
return sum(c, d) - sum(a - 1, d) - sum(c, b - 1) + sum(a - 1, b - 1);
}
}
如有错误,欢迎指出!!!!