lc1619.去掉前后5%
class Solution {
public:
double trimMean(vector<int>& arr) {
int len = arr.size() * 0.05;
sort(arr.begin(), arr.end());
double sum = 0;
for(int i = len; i < arr.size() - len; i++){
sum += arr[i];
}
return sum / (arr.size() - 2 * len);
}
};
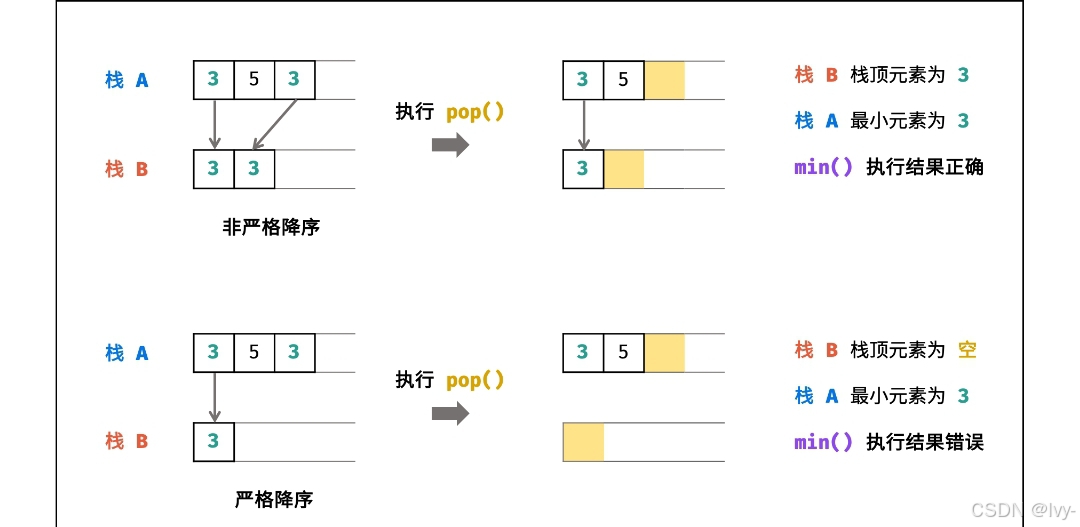
lcr147.最小栈
通过两个栈 维护实现
class MinStack {
public:
stack<int> A, B;
MinStack() {}
void push(int x) {
A.push(x);
if(B.empty() || B.top() >= x)
B.push(x);
}
void pop() {
if(A.top() == B.top())
B.pop();
A.pop();
}
int top() {
return A.top();
}
int getMin() {
return B.top();
}
};
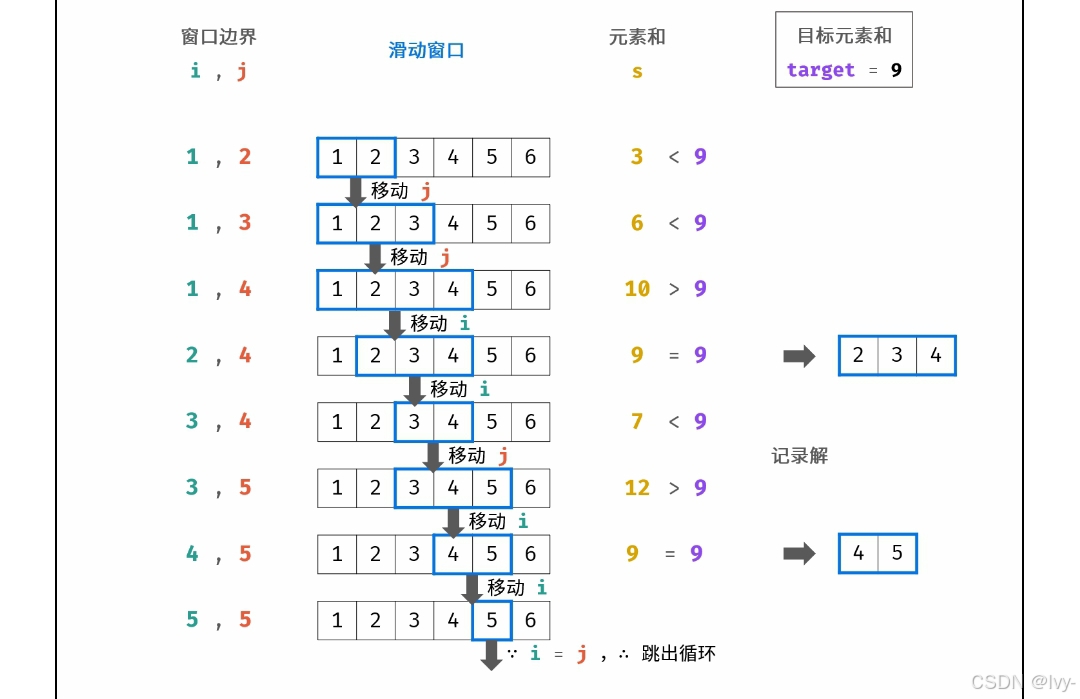
lcr180
特判,放在循环执行的前面
class Solution {
public:
vector<vector<int>> fileCombination(int target) {
int i = 1, j = 2, s = 3;
vector<vector<int>> res;
while(i < j) {
if(s == target) {
vector<int> ans;
for(int k = i; k <= j; k++)
ans.push_back(k);
res.push_back(ans);
}
if(s >= target) {
s -= i;
i++;
} else {
j++;
s += j;
}
}
return res;
}
};
lc973
数据结构vector<pair<double,pair<int,int>>>cnt
sort后取出k个
ans.push_back(vector<int>{cnt[i].second.first, cnt[i].second.second});
class Solution {
public:
double dist(vector<int>&a){
return sqrt(a[0] * a[0] + a[1] * a[1]);
}
vector<vector<int>> kClosest(vector<vector<int>>& points, int k)
{
vector<pair<double, pair<int,int>>>cnt;
for(int i = 0; i < points.size(); i++){
double d = dist(points[i]);
cnt.push_back({d, {points[i][0], points[i][1]}});
}
//按照坐标点进行升序排序
sort(cnt.begin(), cnt.end(), [](pair<double,pair<int,int>>&a,pair<double,pair<int,int>>&b)
{
return a.first < b.first;
});
//记录答案
vector<vector<int>>ans;
for(int i = 0; i < k; i++)
{
ans.push_back(vector<int>{cnt[i].second.first, cnt[i].second.second});
}
return ans;
}
};
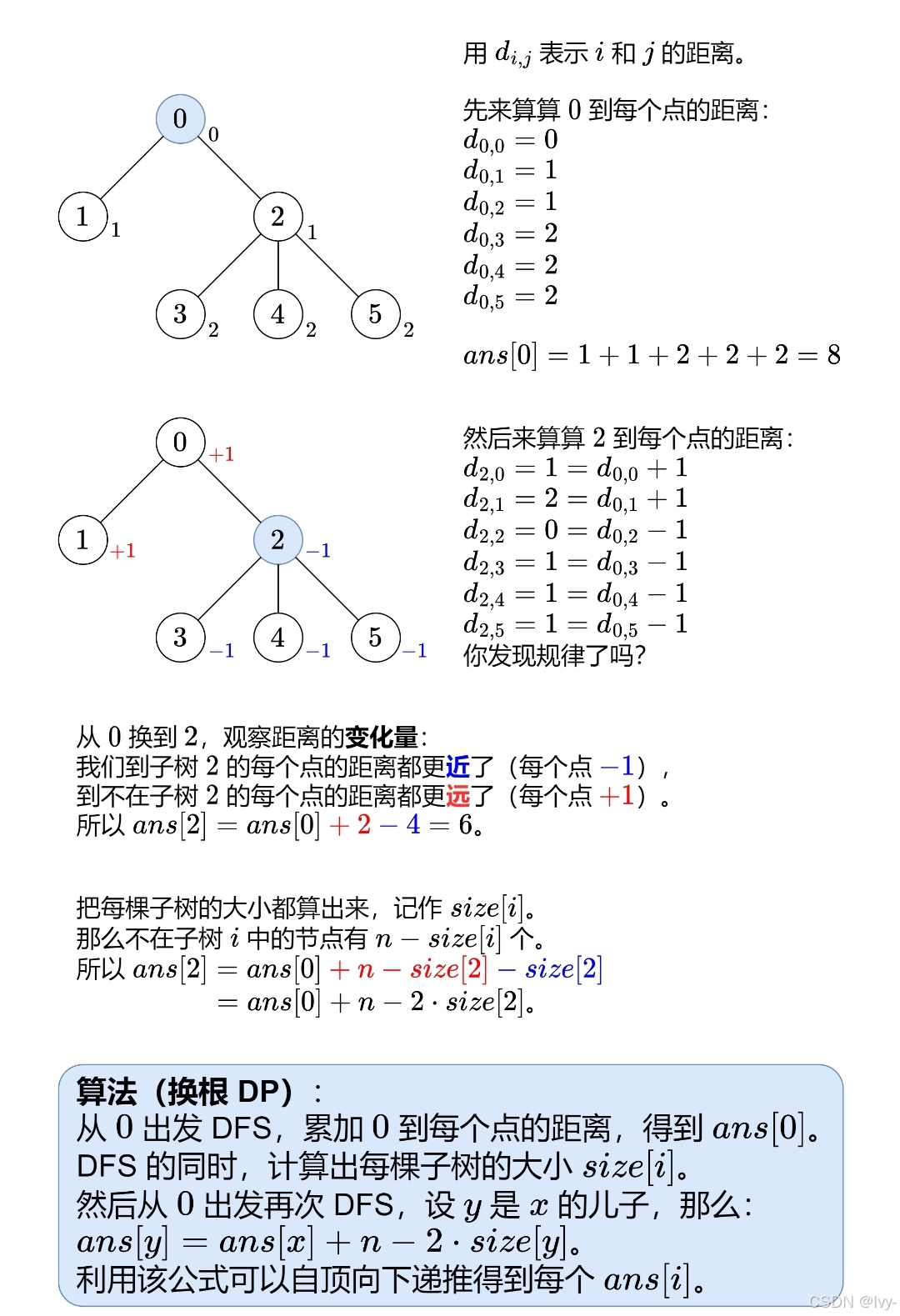
换根dp
最开始想到的是bfs的暴力遍历,也能归纳出数学关系优化
题解是由 父子关系-> 加减关系-dp tree
正解
详见oi-wiki dp tree
class Solution {
public:
vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {
vector<vector<int>> g(n); // g[x] 表示 x 的所有邻居
for (auto& e: edges) {
int x = e[0], y = e[1];
g[x].push_back(y);
g[y].push_back(x);
}
vector<int> ans(n);
vector<int> size(n, 1); // 注意这里初始化成 1 了,下面只需要累加儿子的子树大小
auto dfs = [&](auto&& dfs, int x, int fa, int depth) -> void {
ans[0] += depth; // depth 为 0 到 x 的距离
for (int y: g[x]) { // 遍历 x 的邻居 y
if (y != fa) { // 避免访问父节点
dfs(dfs, y, x, depth + 1); // x 是 y 的父节点
size[x] += size[y]; // 累加 x 的儿子 y 的子树大小
}
}
};
dfs(dfs, 0, -1, 0); // 0 没有父节点
auto reroot = [&](auto&& reroot, int x, int fa) -> void {
for (int y: g[x]) { // 遍历 x 的邻居 y
if (y != fa) { // 避免访问父节点
ans[y] = ans[x] + n - 2 * size[y];
reroot(reroot, y, x); // x 是 y 的父节点
}
}
};
reroot(reroot, 0, -1); // 0 没有父节点
return ans;
}
};
数学归纳法

lc2944.选不选
遍历i,
for j 处理其影响范围,每步取最小的cache
o n^2,但是可以正向遍历,挺好想的

class Solution {
public:
int minimumCoins(vector<int>& prices) {
int n = prices.size();
vector<int> dp(n + 1, 0x3f3f3f3f);
dp[0] = 0;
for (int i = 1; i <= n; ++i)
{
int end = min(2 * i, n);
//处理其影响范围,每步取最小的cache
for (int j = i; j <= end; ++j)
{
dp[j] = min(dp[j],dp[i - 1] + prices[i - 1]);
}
}
return dp[n];
}
};
