数据结构：二叉树的链式存储

用链表来表示一棵二叉树，即用指针指向来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。

我们之前就已经说过，二叉树是递归定义的，也就是说，一棵二叉树是由根节点，左子树，右子树组成的，而左子树和右子树本身又是一棵二叉树。我们要牢记二叉树是递归定义的这一特点，在后续操作中我们将会体会递归的暴力美学。

二叉树的前中后序遍历

前序遍历（先根遍历）：先遍历根节点，再遍历左子树，最后遍历右子树。（根左右）

中序遍历（中根遍历）：先遍历左子树，再遍历根节点，最后遍历右子树。（左根右）

后序遍历（后根遍历）：先遍历左子树，再遍历右子树，最后再遍历根节点。（左右根）

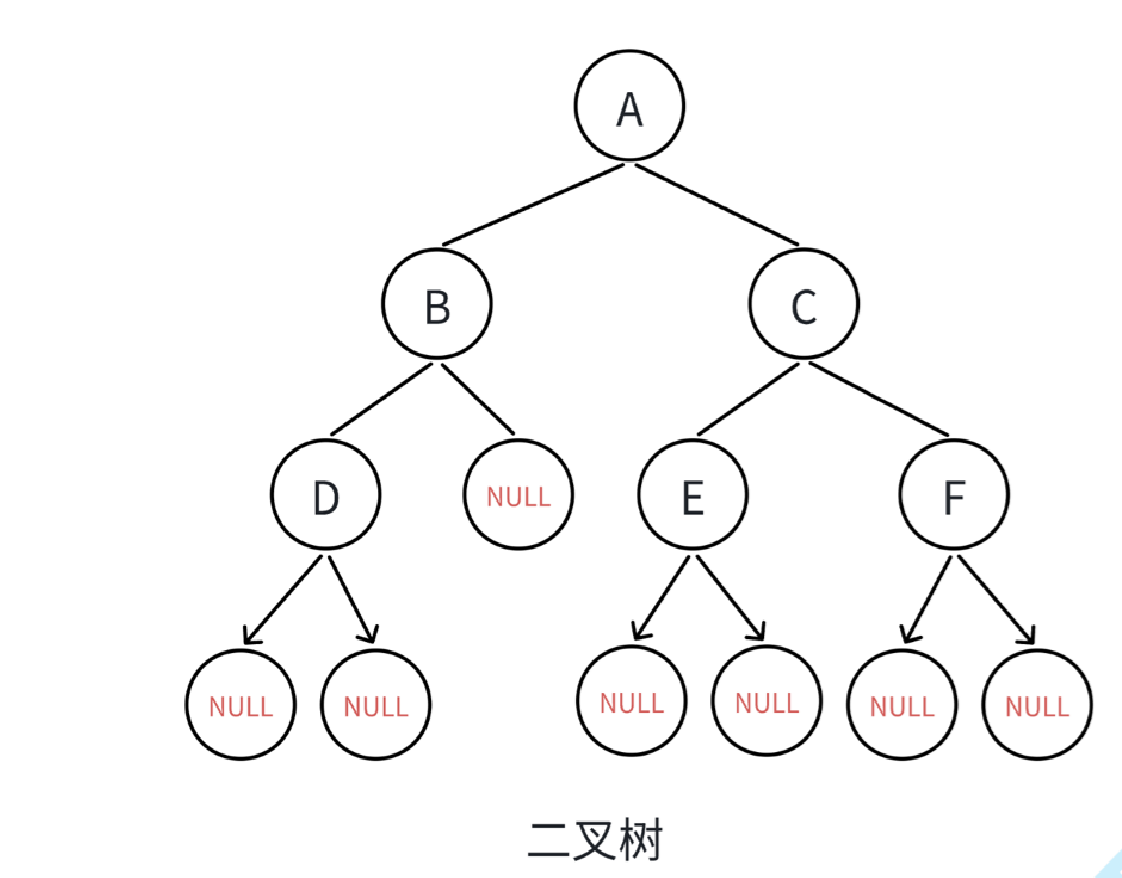
根据上述定义，写出这个二叉树分别按三种遍历方式得到的序列：

二叉树相关方法的代码实现

二叉树的结构

//定义树的结构
typedef char btdatatype;

typedef struct btnode
{
	btdatatype data;  //节点数据
	struct btnode* left;//左孩子结点
	struct btnode* right;//右孩子结点
}btnode;

二叉树节点的创建

//建立新的树节点
btnode* buynode(btdatatype x)
{
	btnode* newnode = (btnode*)malloc(sizeof(btnode));
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;
}

二叉树的前序遍历

//前序遍历树的节点
void preorder(btnode* root)
{
	//递归的终止条件：遍历到空节点
	if (root == NULL)
	{
		return;
	}
	//先访问根节点
	printf("%c ", root->data);
	//再遍历左子树
	preorder(root->left);
	//再遍历右子树
	preorder(root->right);
}

画图说明递归过程（红色的线表示递推，绿色的线表示回归，递推就意味着要创建函数栈桢，回归表示函数栈桢销毁，同时要返回值）：

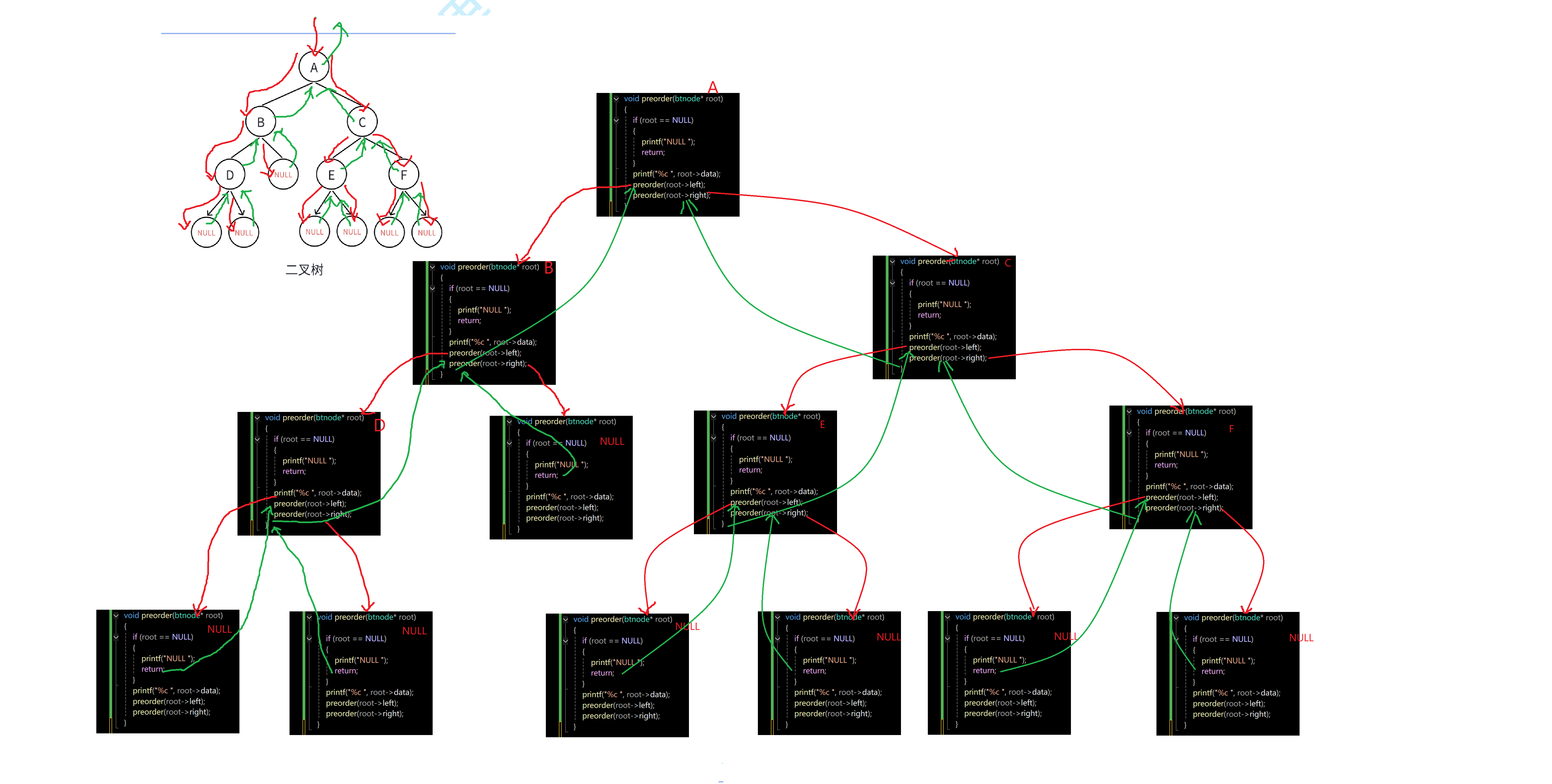
二叉树的中序遍历

//中序遍历树的节点
void inorder(btnode* root)
{
	if (root == NULL)
	{
		return;
	}
	//先遍历左子树
	inorder(root->left);
	//再访问根节点
	printf("%c ", root->data);
	//再遍历右子树
	inorder(root->right);
}

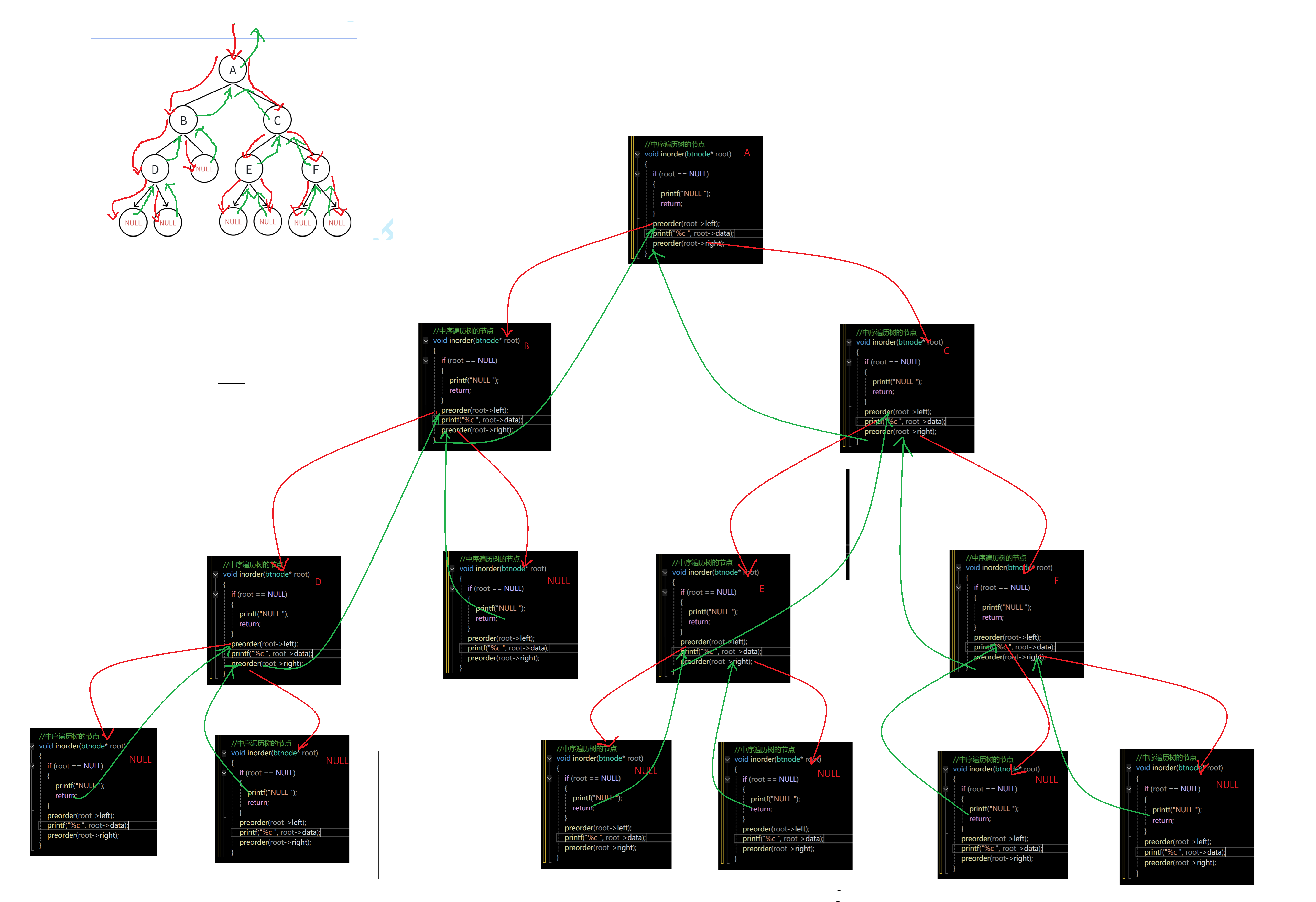
在前面两个递归过程的解释中，我们发现，在递归调用时，产生的函数栈桢形成的结构与二叉树的形态结构长得一模一样，所以接下来我们模拟递归过程的函数栈桢的调用时，就不用再使用具体的函数栈桢图了，可以直接使用二叉树的每个节点来进行模拟比较。

二叉树的后序遍历

//后序遍历树的节点
void postorder(btnode* root)
{
    if (root == NULL)
    {
        return;
    }
    //先遍历左子树
    postorder(root->left);
    //再遍历右子树
    postorder(root->right);
    //最后访问根节点
    printf("%c ", root->data);
}

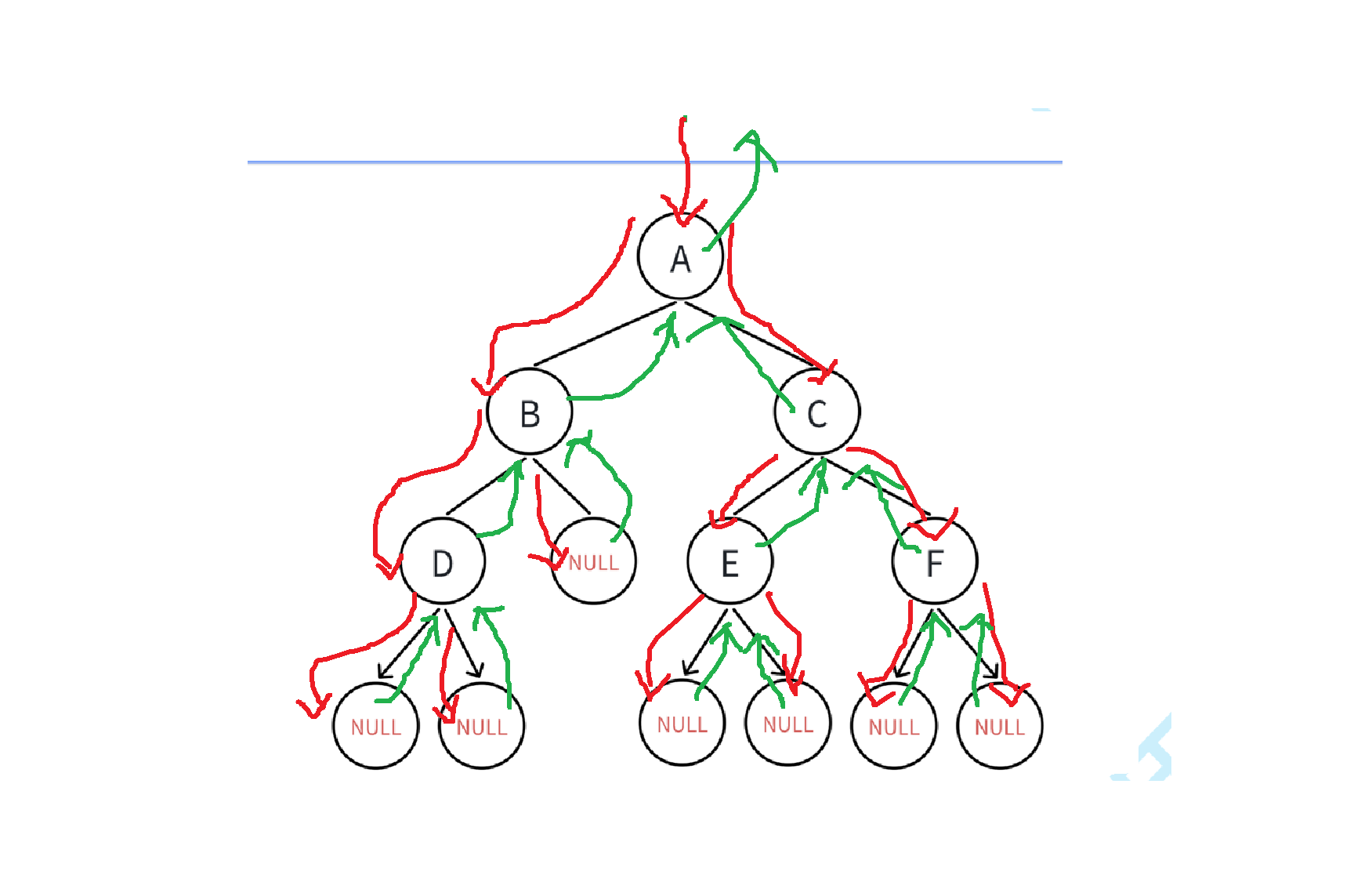
三种遍历方式下，产生的函数栈桢图一样。

二叉树中结点的个数

//二叉树节点个数
void binarytreesize_1(btnode* root, int size)
{
	if (root == NULL)
	{
		return;
	}
	size++;
	binarytreesize_1(root->left, size);
	binarytreesize_1(root->right, size);
}

大家看看上面的代码能正确完成任务嘛，我们可以再写一个测试代码来测试一下：

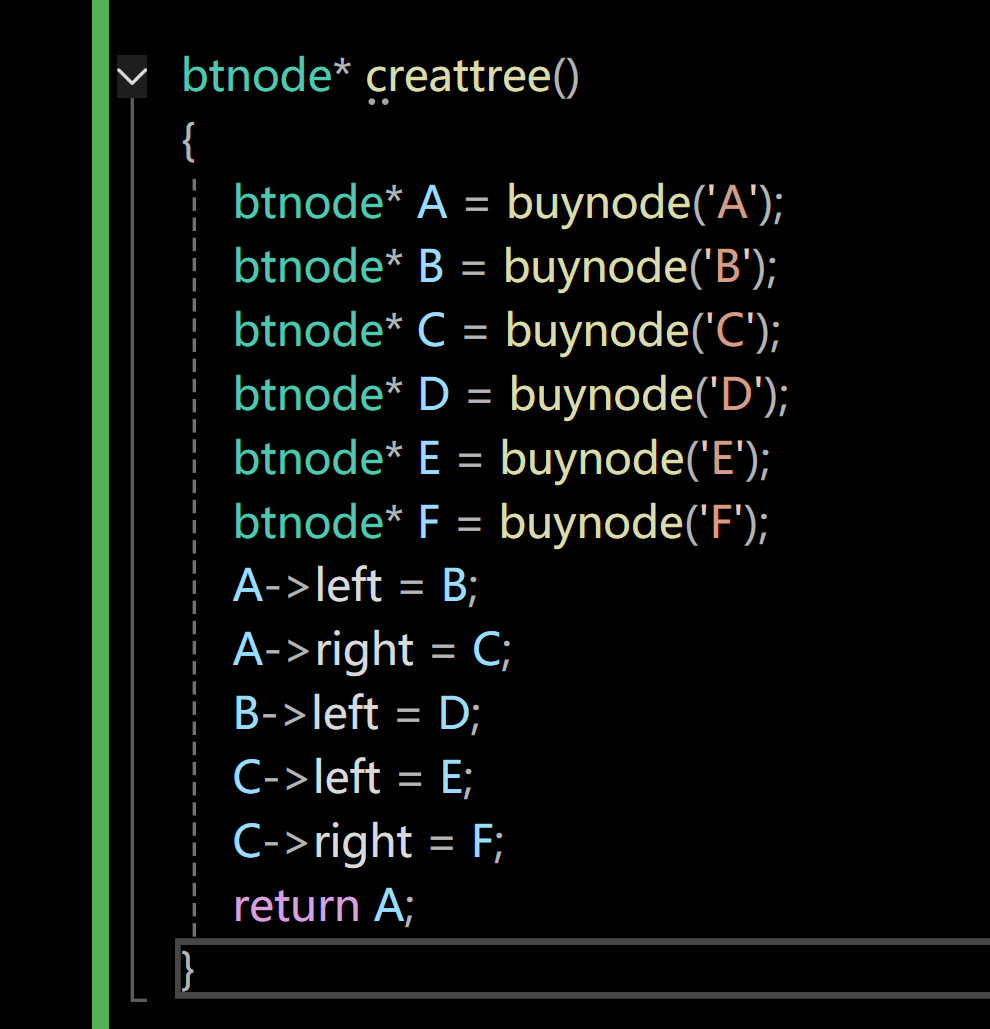
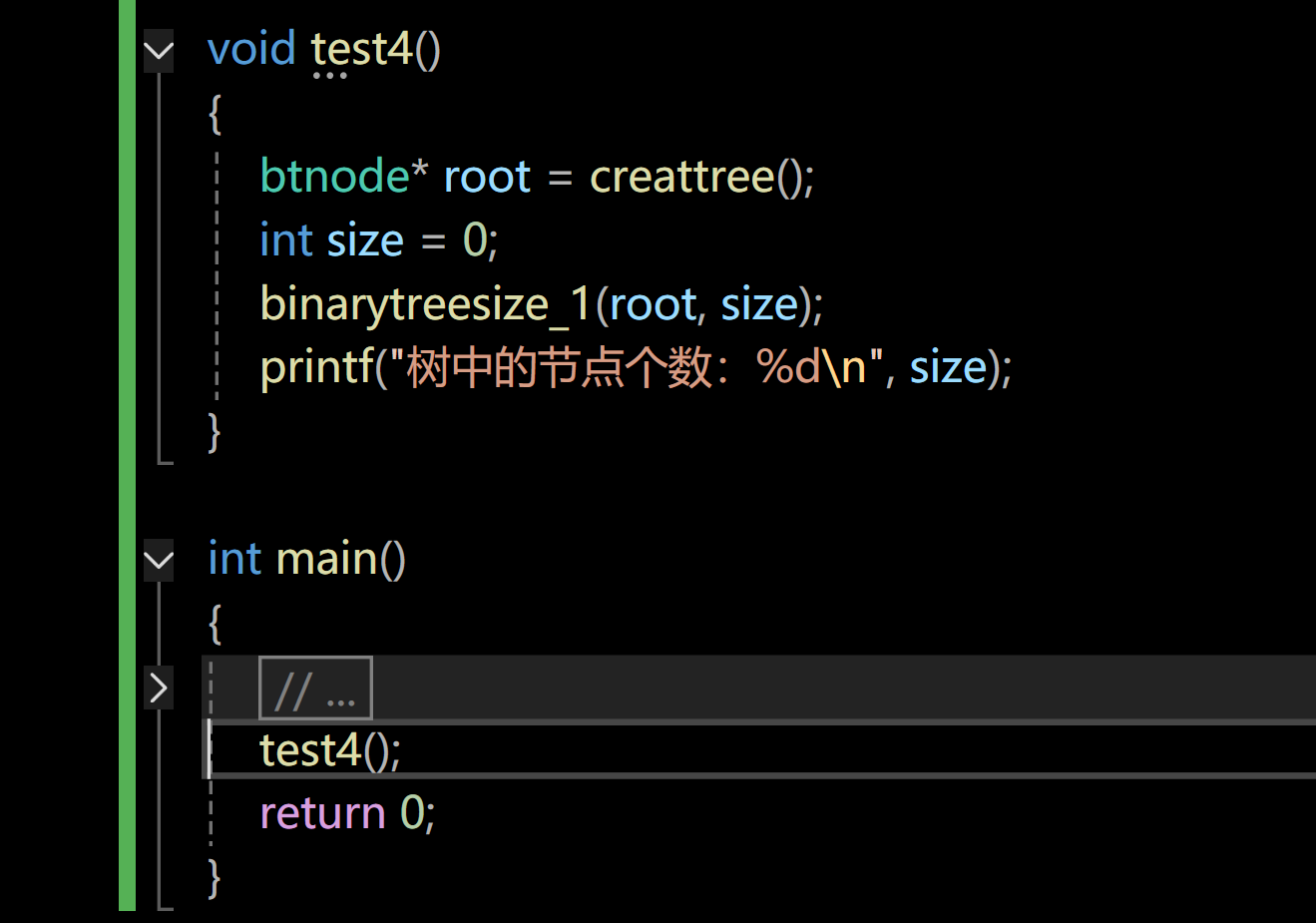
屏幕前的家人们觉得结果会是6嘛？

上面的代码应该是想实现在递归过程中只要遇到的节点不是空节点就对size进行累加，而且我们传入的size的初始值是0，按理来说应该会完成任务，但是size的大小竟然没有发生改变。

这是因为，我们采用的是传值调用，形参的改变不会影响实参，所以size的值不会发生改变，还是0.但我们也得到了解决思路，直接采用传址调用就好了呀：

void binarytreesize_2(btnode* root, int* psize)
{
	if (root == NULL)
	{
		return;
	}
	(*psize)++;
	binarytreesize_2(root->left, psize);
	binarytreesize_2(root->right, psize);
}

我们用相同的测试用例测试一下结果：

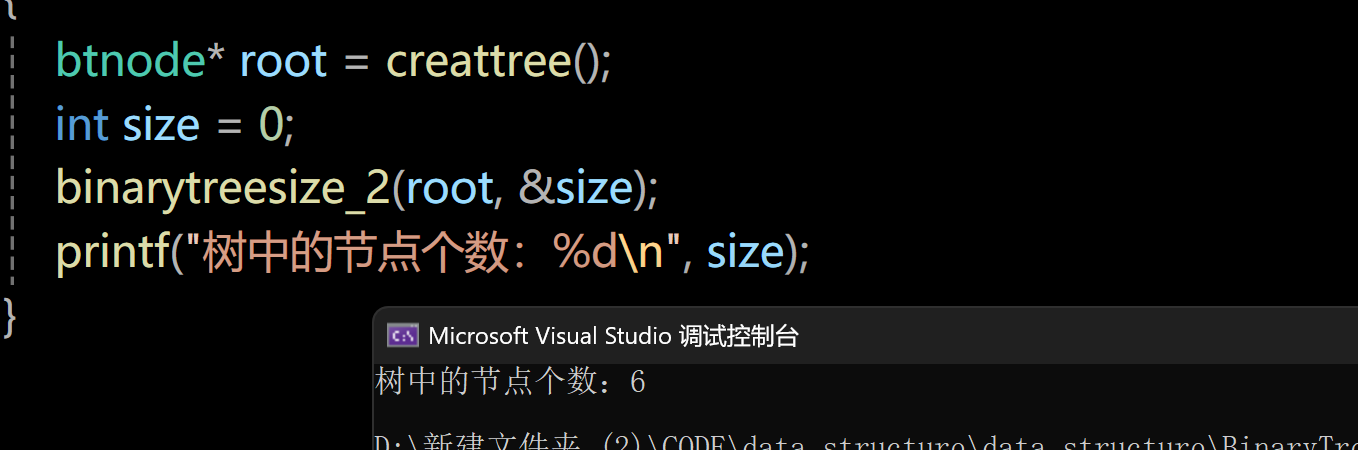
看来这个代码好像确实可以帮我们完成任务。

上面代码的递归过程图解：

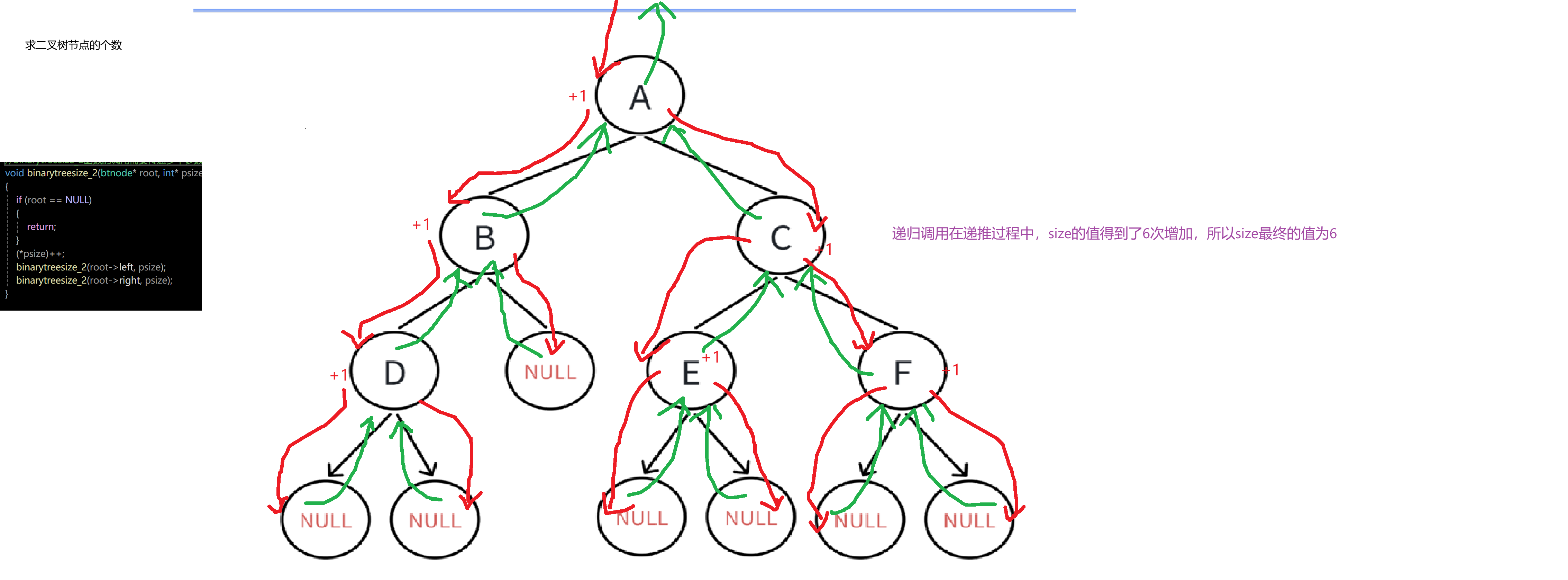
如果我们在多测试几次代码：

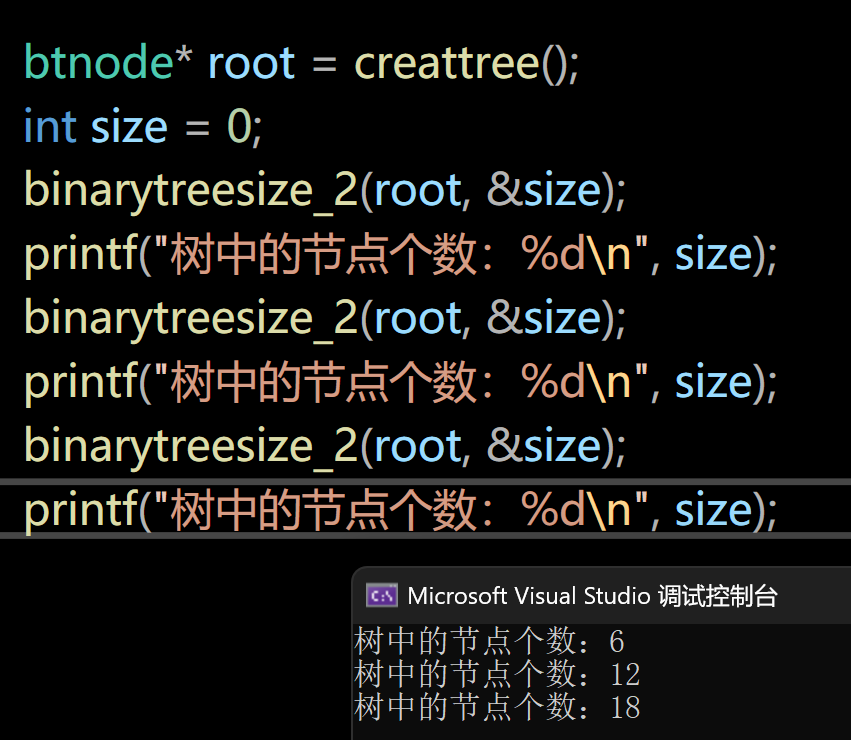
我们会发现size的值在不断递增，这是因为第二次和第三次调用函数时，我们没有将size重新赋值为0，直接在原来值“6”的基础上进行累加了，这也正是我们这个代码的缺点所在：每一次调用函数前都要将size的值重新置为0.

那还有没有别的算法解决问题呢，有的兄弟们，有的。

我们知道，二叉树是递归定义的，它是由根节点、左子树、右子树组成。要求整棵二叉树节点个数，不就是求根节点的个数加上左子树中节点的个数再加上右子树中节点的个数嘛，而根节点的个数本来就是1，这样我们就把一个大问题拆解成相似的小问题了，这种情况下，使用递归简直就不要太容易了。

int binarytreesize(btnode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return 1 + binarytreesize(root->left) + binarytreesize(root->right);
}

我们再来用相同的测试用例测试一下：

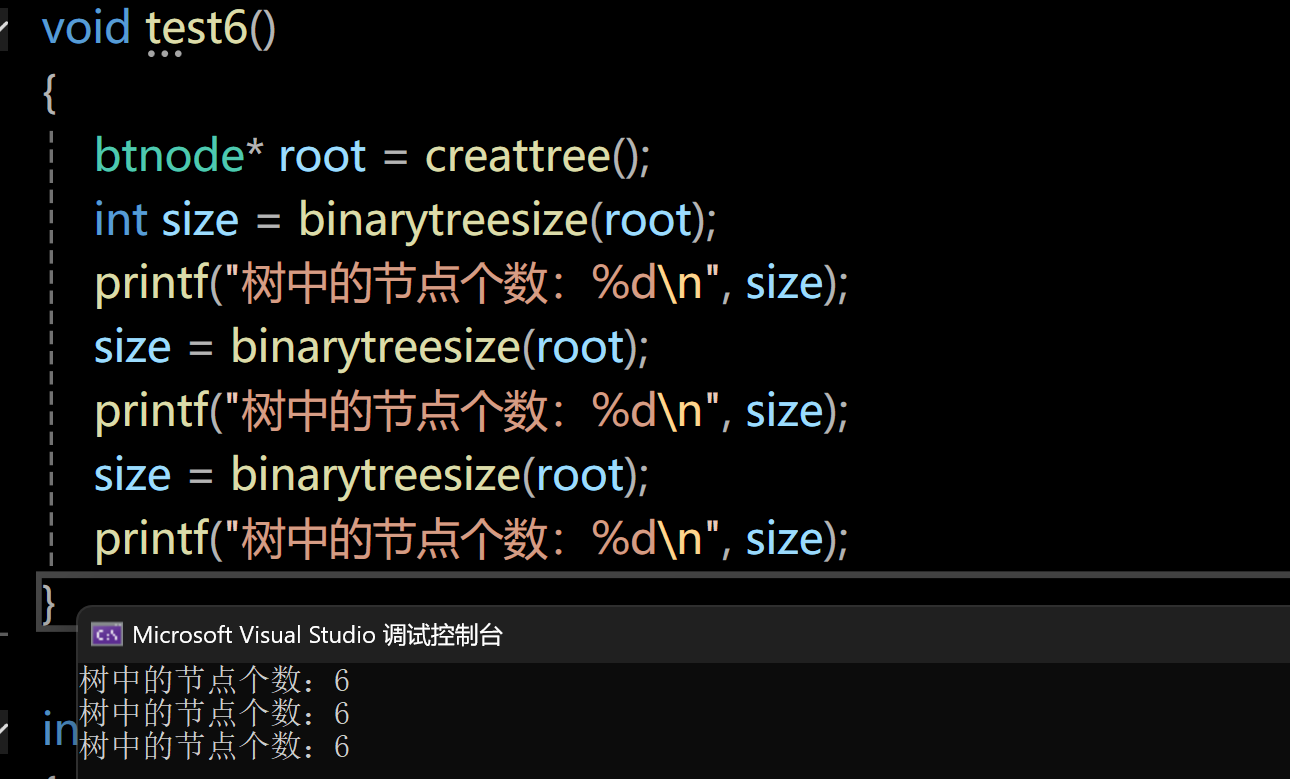
可以看到，这个代码可以通过测试样例，同时避免了上一个代码的缺点。

再来模拟一下递归调用的过程：

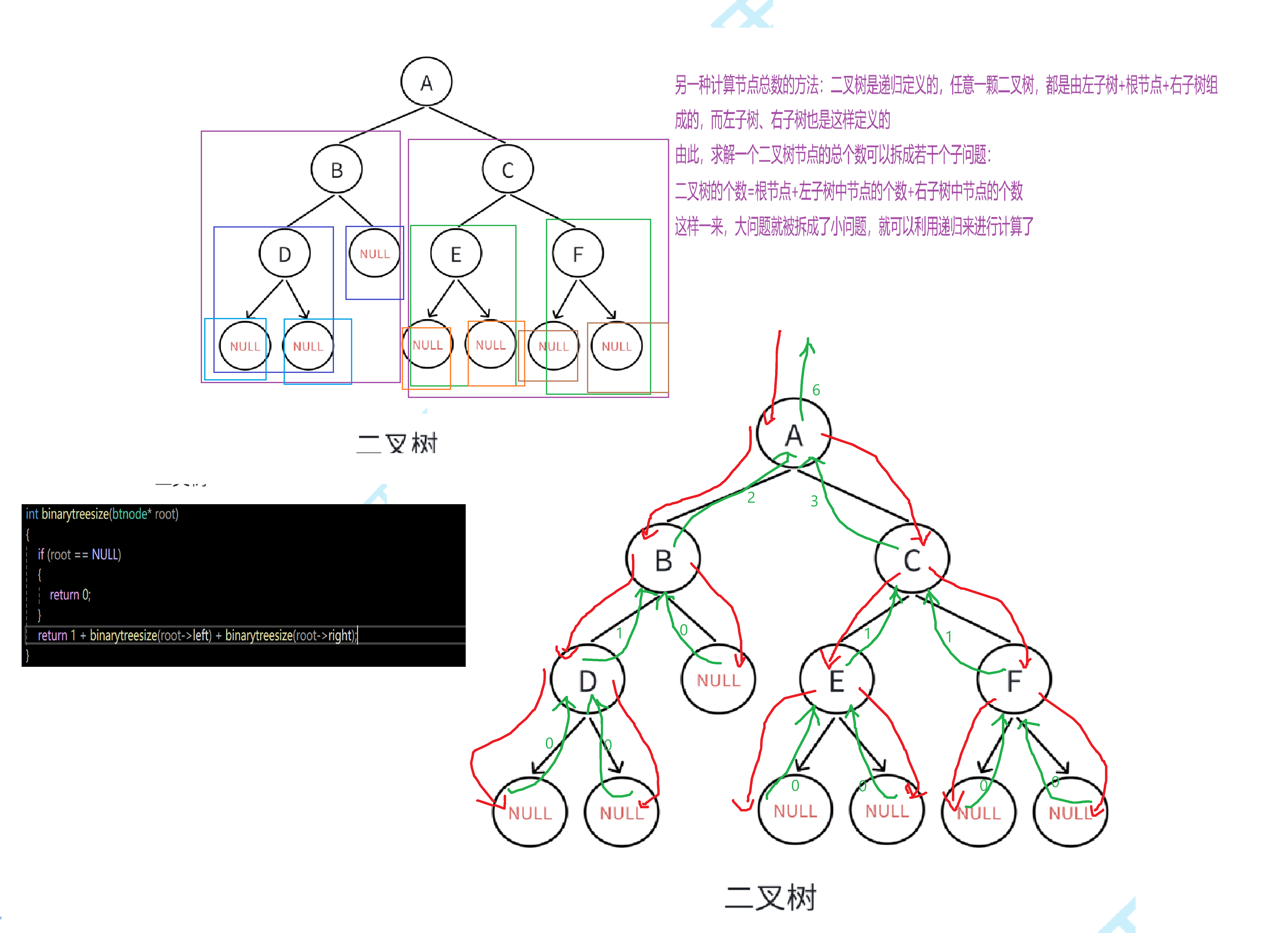
二叉树中叶子结点的个数

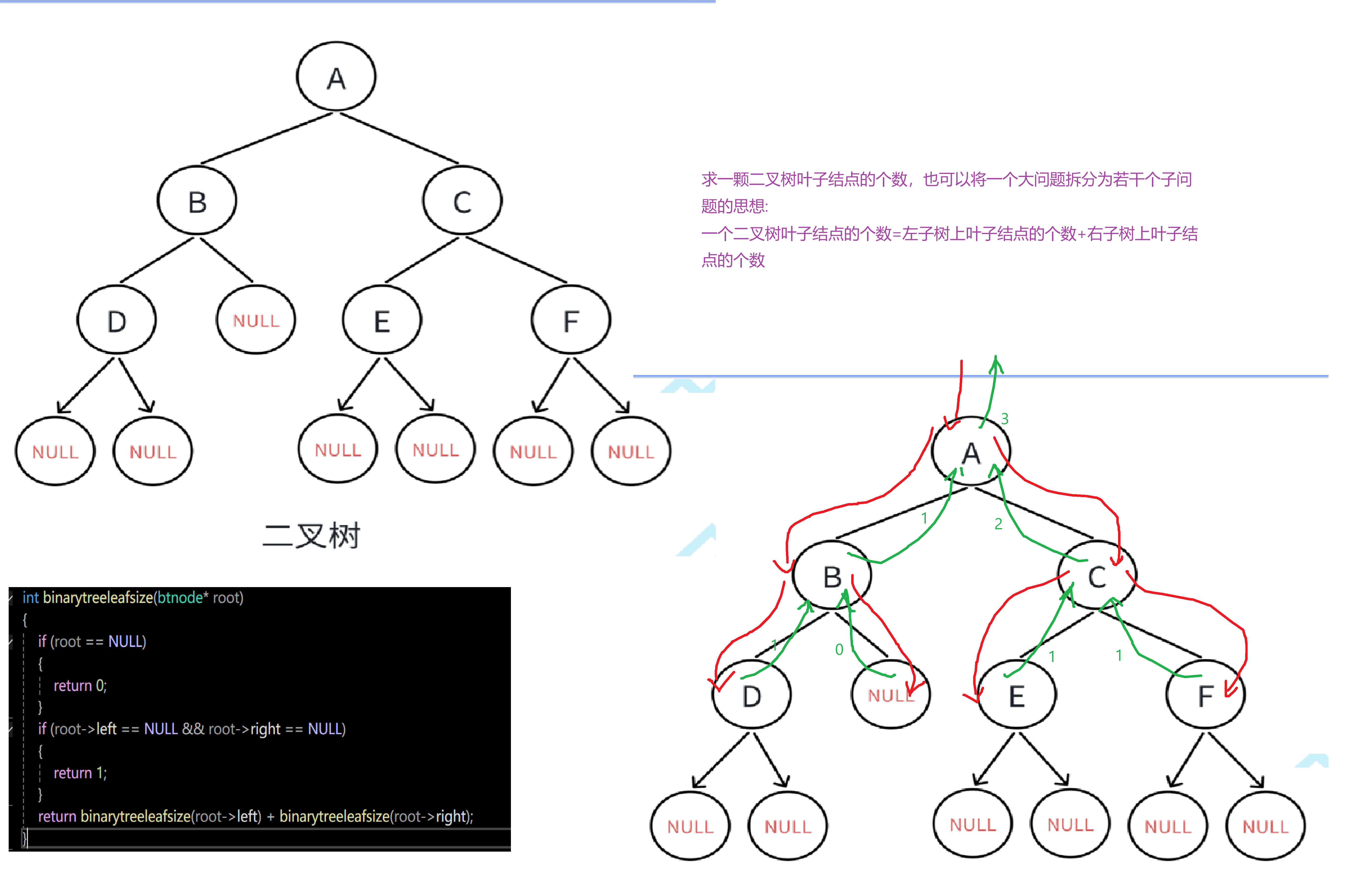
//二叉树叶子结点个数
int binarytreeleafsize(btnode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return binarytreeleafsize(root->left) + binarytreeleafsize(root->right);
}

求第k层节点的个数

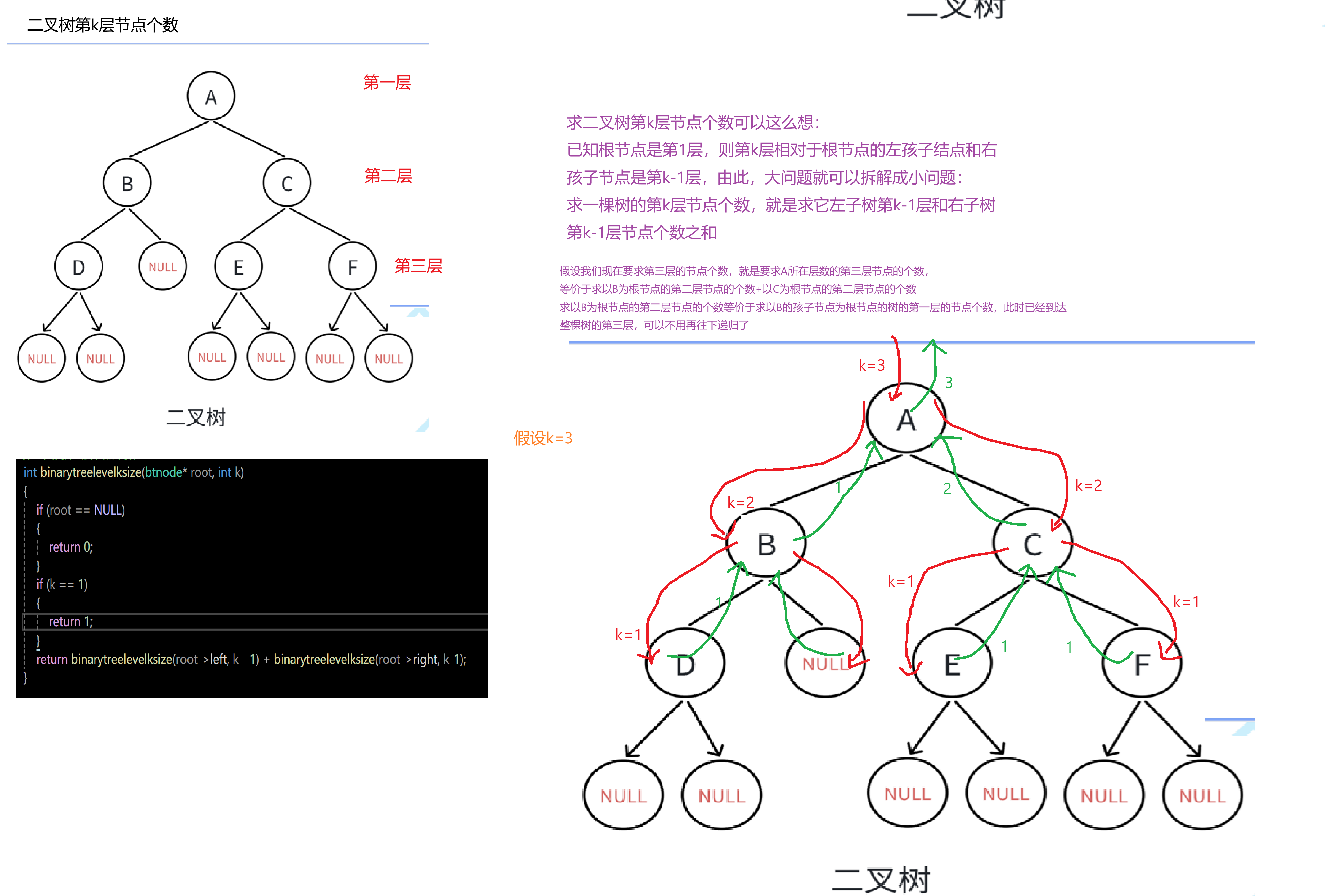
//二叉树第k层节点个数
int binarytreelevelksize(btnode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)//树的根在第一层
	{
		return 1;
	}
	return binarytreelevelksize(root->left, k - 1) + binarytreelevelksize(root->right, k - 1);
}

求二叉树的深度

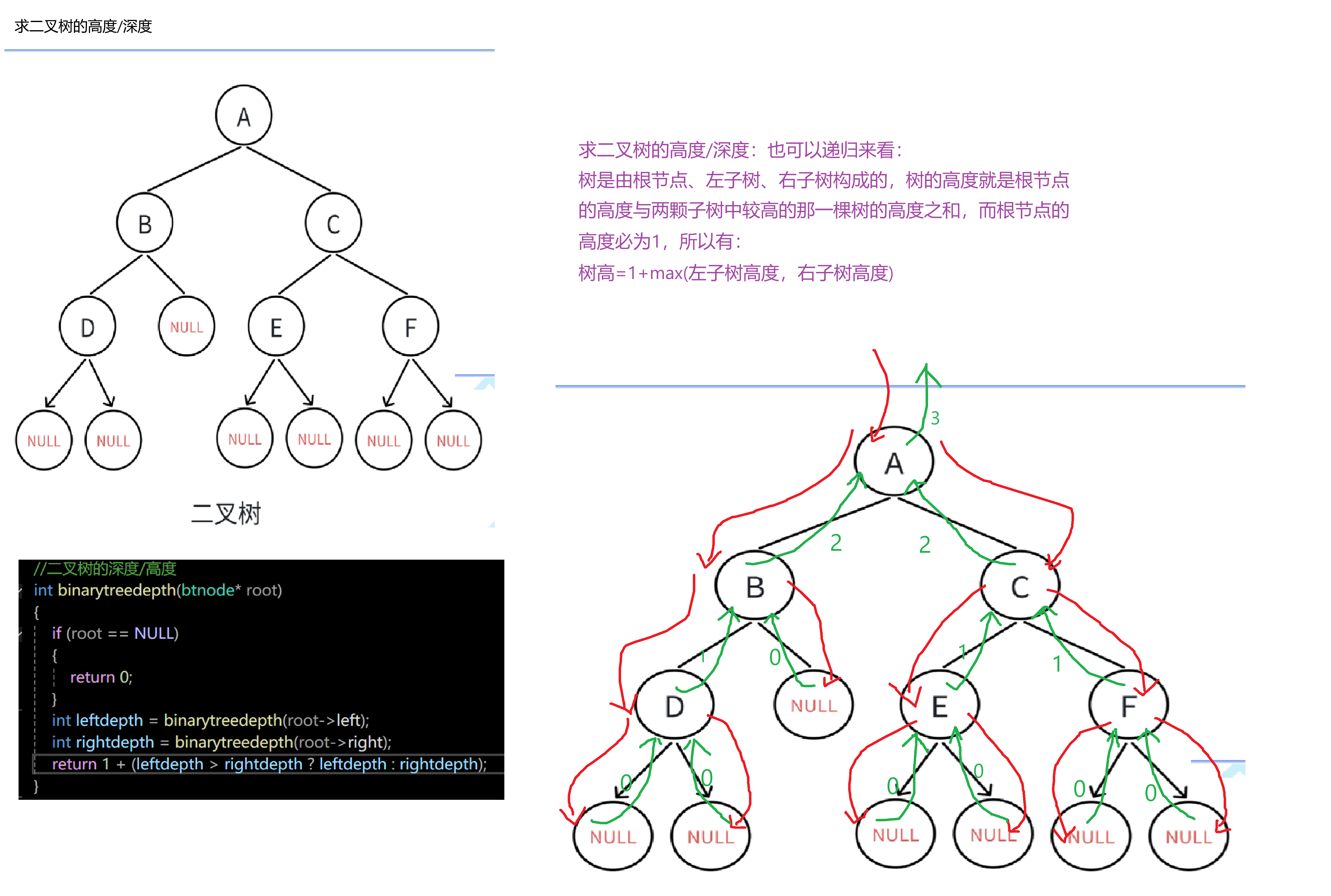
//二叉树的深度/高度：深度从1开始哦
int binarytreedepth(btnode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftlen = binarytreedepth(root->left);
	int rightlen = binarytreedepth(root->right);
	return 1 + (leftlen > rightlen ? leftlen : rightlen);
}

在树中查找节点

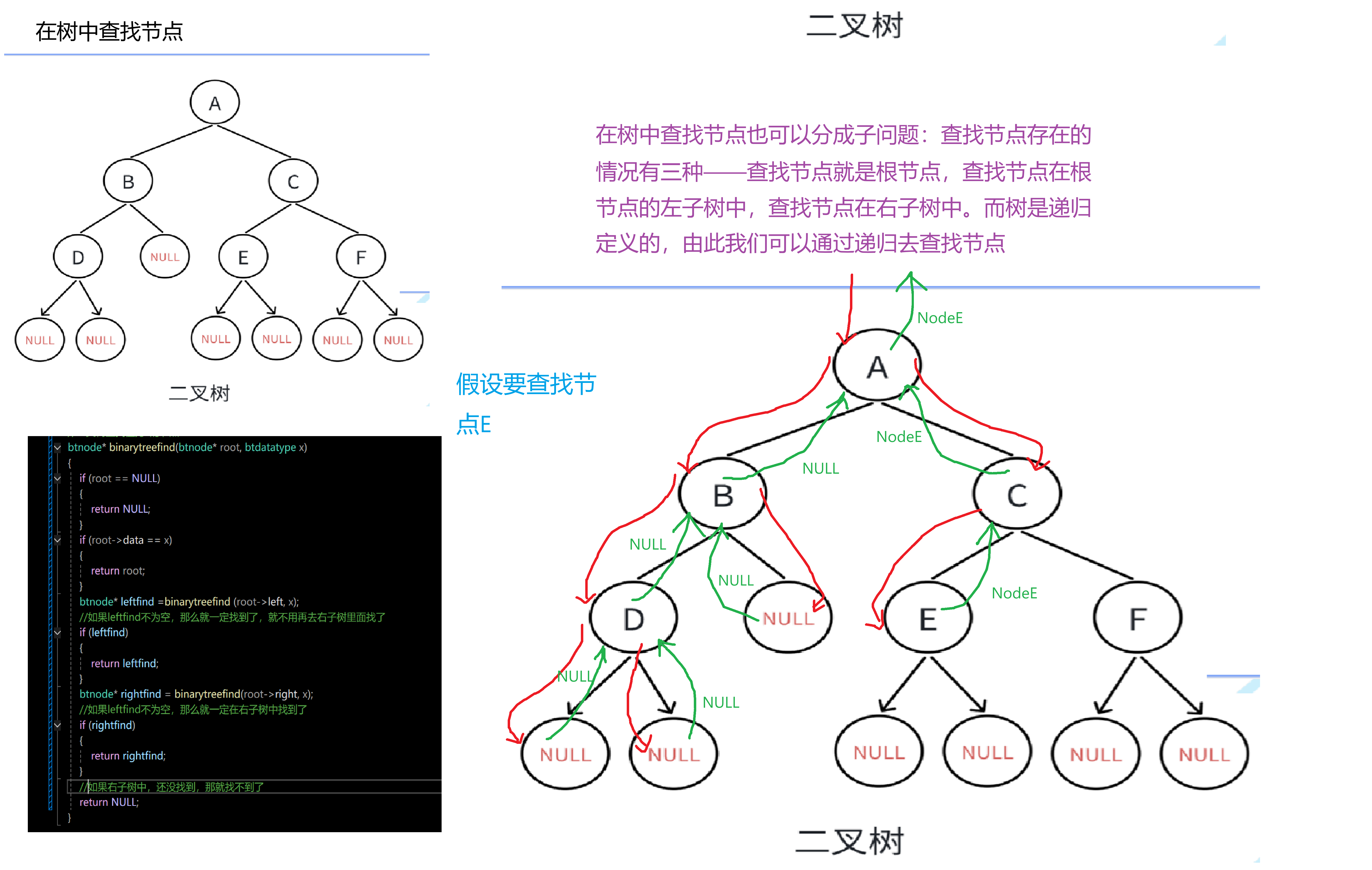
//二叉树查找值为x的节点
btnode* binarytreefind(btnode* root, btdatatype x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	//如果在左子树中找到了，就不用在右子树中找了
	btnode* leftfind = binarytreefind(root->left, x);
	if (leftfind)
	{
		return leftfind;
	}
	//说明左子树中没有找到
	//再到右子树中继续找
	btnode* rightfind = binarytreefind(root->right, x);
	if (rightfind)
	{
		return rightfind;
	}
	//说明右子树中也没有找到
	return NULL;
}

二叉树的销毁

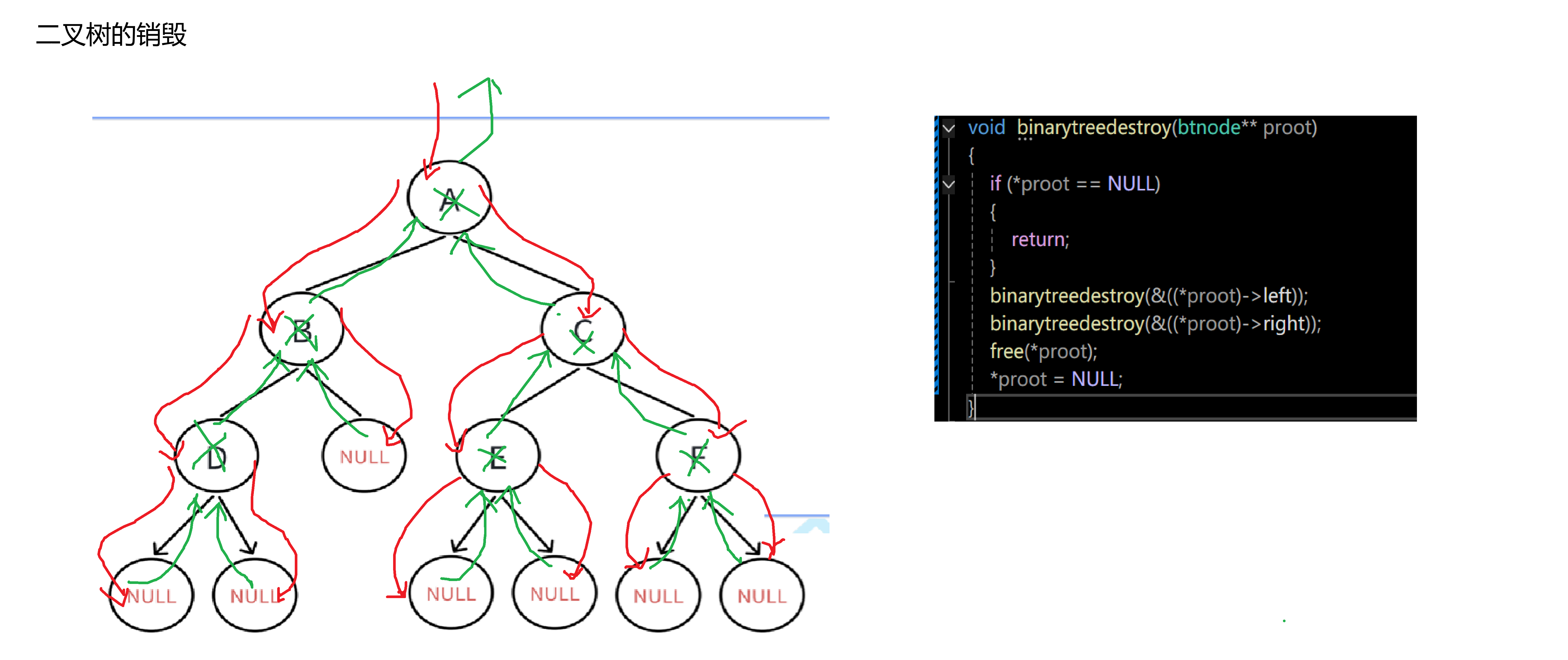
//二叉树的销毁
//二叉树的销毁:要销毁二叉树，肯定是要先遍历二叉树，那么我们应该如何遍历二叉树呢？
//可以参考已有的遍历方式：前序？中序？后序？
//前序和中序在遍历完子树前都会先遍历完根，先销毁根的话，就没办法再找到根的子树了，所以这两种遍历方式都不可取，我们只能后序遍历来销毁二叉树
void  binarytreedestroy(btnode** proot)
{
	if (*proot == NULL)
	{
		return;
	}
	binarytreedestroy(&((*proot)->left));
	binarytreedestroy(&((*proot)->right));
	free(*proot);
	*proot = NULL;
}

二叉树的层序遍历

二叉树的层序遍历是指 按照树的层级顺序，从上到下、从左到右依次访问所有节点。这种遍历方式也称为 广度优先搜索（BFS），通常需要借助 队列 数据结构来实现。

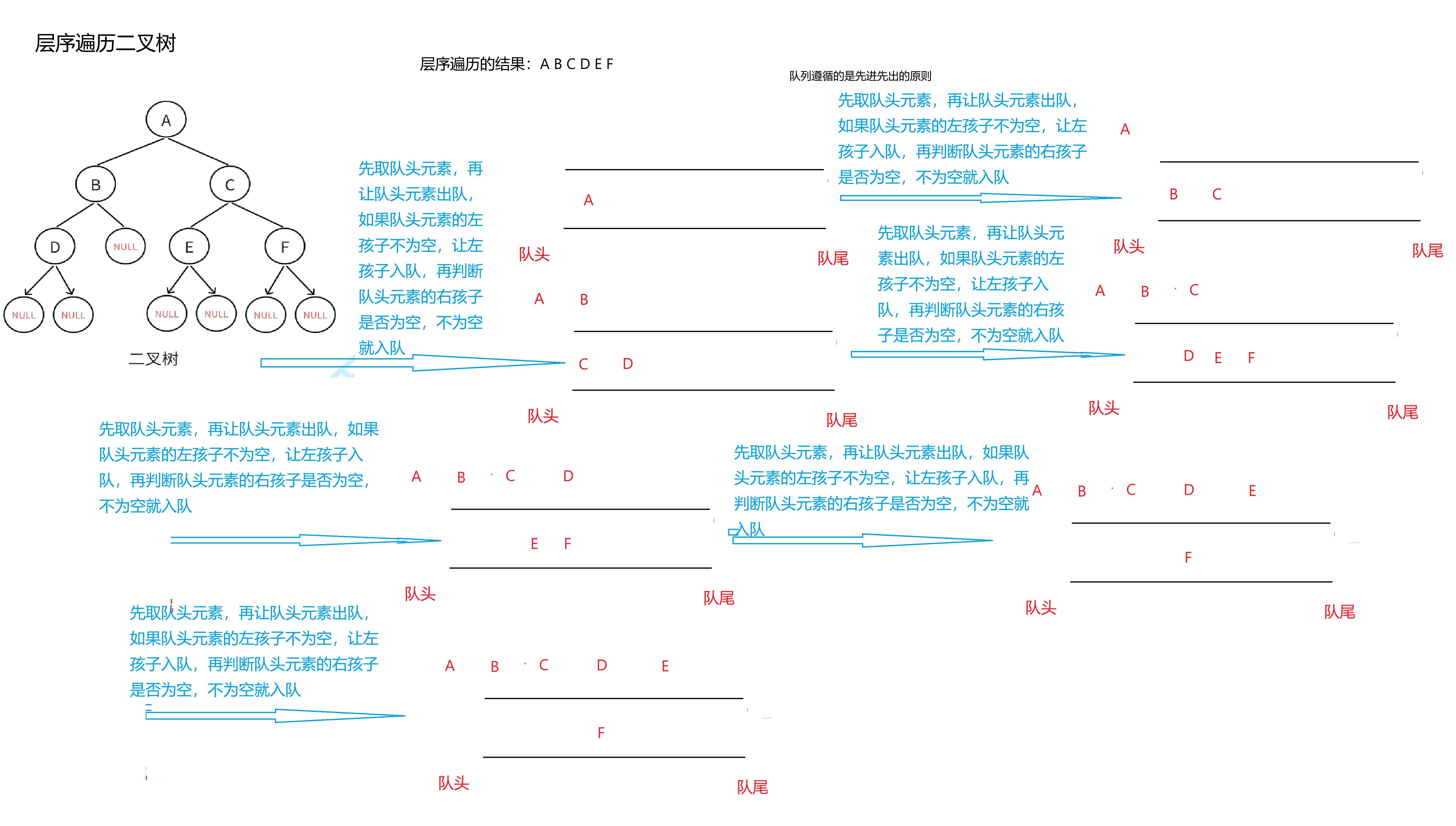
在这个层序遍历的实现中，我们需要使用队列来辅助，所以我们之前写的队列的实现方法就派上用场了，还没看的朋友可以点击链接：数据结构里的 “排队系统”：队列的生活映射与代码实现-CSDN博客进行观看哦。

如果之前已经实现了队列相关方法的盆友，可以按照以下步骤直接添加：

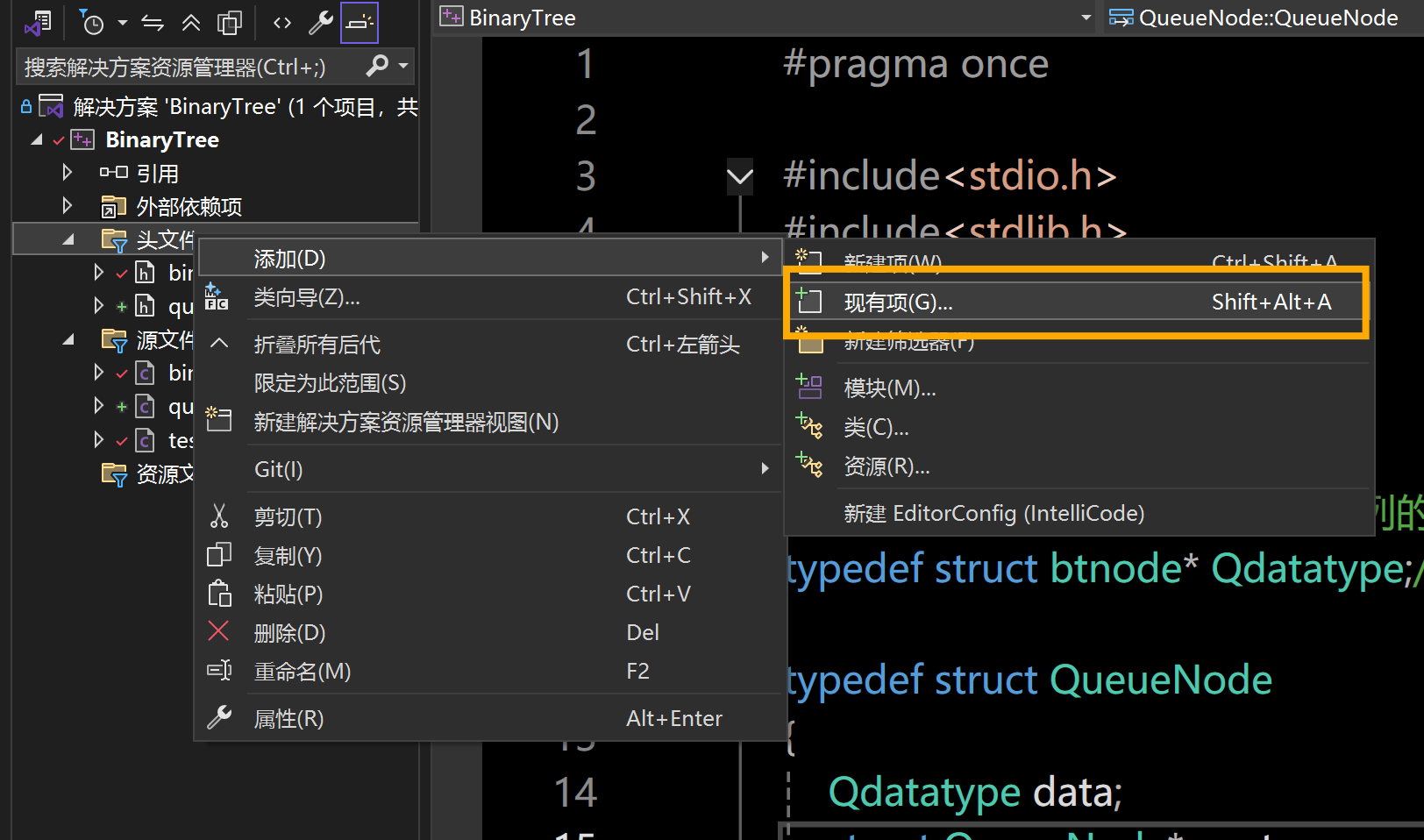
找到解决方案资源管理器->右键单击头文件->添加->现有项->来到你所写的队列的实现方法的项目路径下：

按住ctrl键，选中queue.c和queue.h两个文件，直接ctrl+c复制两个文件，再来到当前二叉树实现方法的路径下，将两个文件粘贴到当前路径：

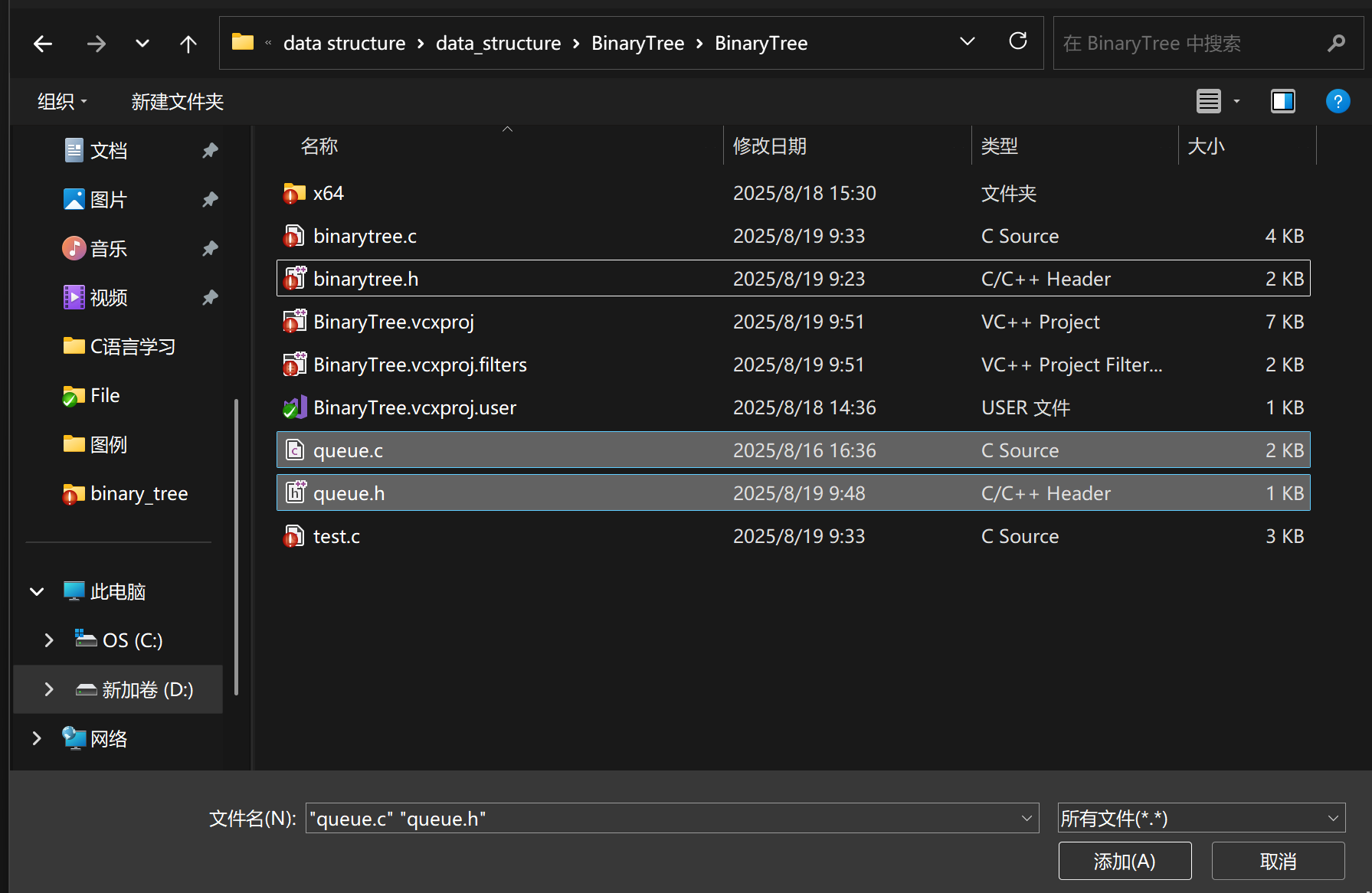
此时两个文件还是选中的状态，我们直接点击添加就好。

添加好以后，将queue.c文件拖拽到源文件的地方就好了。

现在既然我们要是用队列中的相关方法，还要包含对应的头文件，那就要在当前二叉树的项目中的头文件中添加queue.h的头文件包含：

同时，之前我们在实现队列的时候，队列中存储的元素类型是int类型的，现在我们要将它改成二叉树节点类型的，但是队列的实现方法中并没有关于二叉树的结构声明，难道需要在队列实现方法的头文件中加上："include binarytree.h"？这样就会造成头文件的相互包含，就会引发错误，正确的方法就是在queue.h文件中加上这样一句代码：

typedef struct btnode* Qdatatype;

它的作用是：告诉队列：你要存的数据类型是一个指向 struct btnode 的指针，但我不关心它长什么样。换句话说：

• 队列只负责“存指针、传指针”，不关心这个指针指向的结构体有哪些成员。
• 真正的 struct btnode 定义可以放在别的文件里（比如 tree.c），queue.h 不需要知道细节

那现在我们就来手动实现一下层序遍历的代码吧：

//层序遍历
void levelorder(btnode* root)
{
	if (root == NULL)
	{
		return;
	}
	//先创建一个队列
	Queue q;
	QueueInit(&q);
	//先让队头元素入队列
	QueuePush(&q, root);

	//不断循环直到队列为空
	while (!QueueEmpty(&q))
	{
		//先取队头元素
		btnode* top = QueueFront(&q);
		//出队
		QueuePop(&q);
		//访问队头元素
		printf("%c ", top->data);
		//如果左孩子不为空，左孩子入队
		if (top->left)
		{
			QueuePush(&q, top->left);
		}
		//如果右孩子不为空，右孩子入队
		if (top->right)
		{
			QueuePush(&q, top->right);
		}
	}
	QueueDesTroy(&q);
}

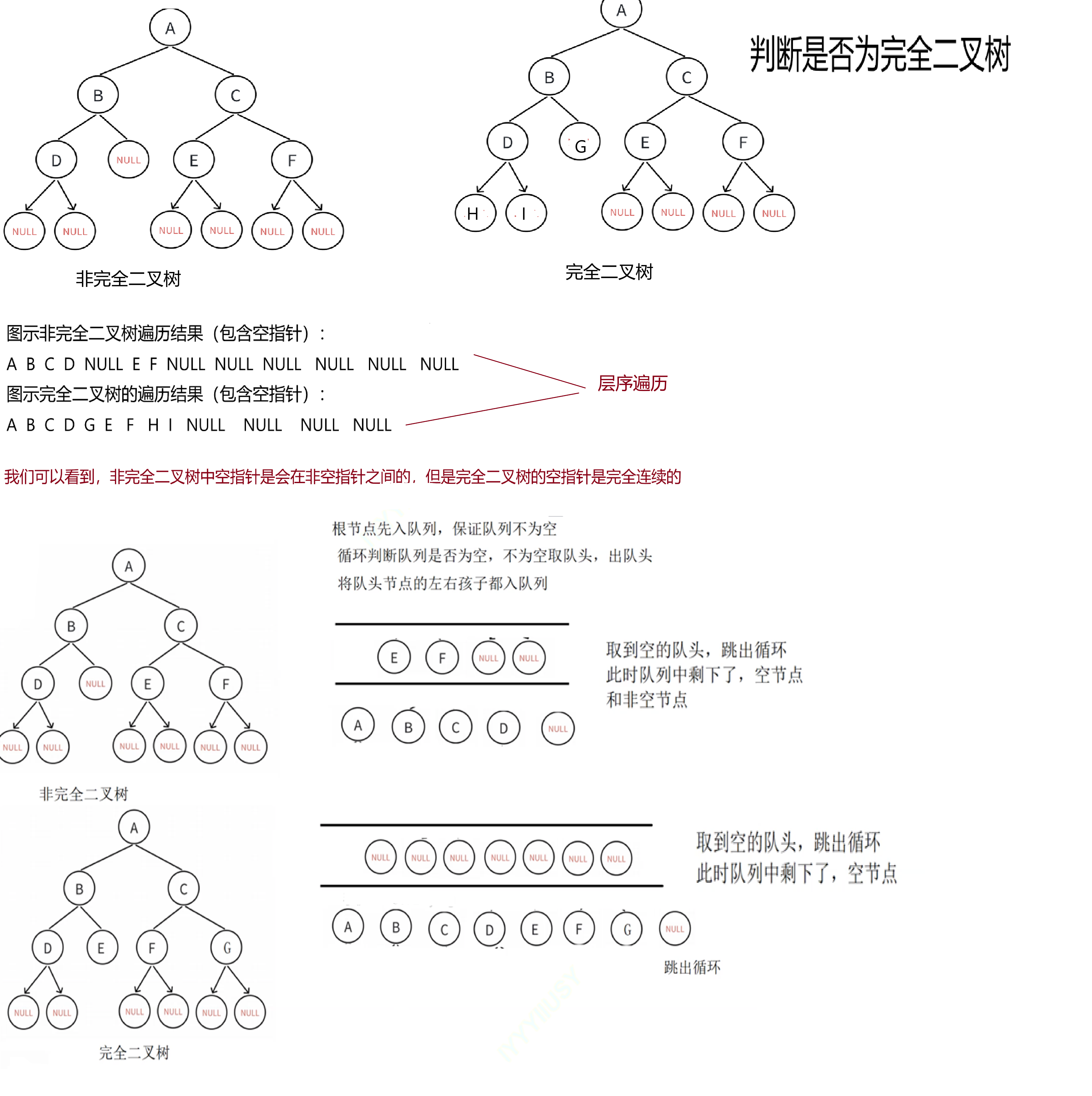
判断是否为完全二叉树

//判断是否为完全二叉树
bool binarytreecomplete(btnode* root)
{
	if (root == NULL)
	{
		return true;
	}
	//利用层序遍历的思想判断是否为完全二叉树
		//先创建一个队列
	Queue q;
	QueueInit(&q);
	//先让队头元素入队列
	QueuePush(&q, root);

	//不断循环直到队列为空
	while (!QueueEmpty(&q))
	{
		//先取队头元素
		btnode* top = QueueFront(&q);
		//出队
		QueuePop(&q);
		//如果队头元素为空，就直接跳出循环
		if (top == NULL)
		{
			break;
		}
	//走到这里，说明队列不为空，那么就让队头元素的左右孩子都入队列
		QueuePush(&q, top->left);
		QueuePush(&q, top->right);
	}

	//现在就只需要判断第一次得到空的队头元素后，剩下的元素是否是既有空节点又有非空节点（非完全二叉树）
	//如果剩下的元素只有空节点（完全二叉树）
	while (!QueueEmpty(&q))
	{
		//取队头元素
		btnode* top = QueueFront(&q);
		QueuePop(&q);
		if (top != NULL)
		{
			QueueDesTroy(&q);
			return false;
		}
	}
	QueueDesTroy(&q);
	return true;
}

今天的内容就是这些，我们可以看到在这一小节中我画了很多图，其实画图是很利于我们理解算法的，小伙伴们自己也要多练练哦!!

代码整合

//binarytree.h
#pragma once

#include"queue.h"
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

//定义树的结构
typedef char btdatatype;

typedef struct btnode
{
	btdatatype data;
	struct btnode* left;
	struct btnode* right;
}btnode;

//建立新的树节点
btnode* buynode(btdatatype x);

//前序遍历树的节点
void preorder(btnode* root);

//中序遍历树的节点
void inorder(btnode* root);

//后序遍历树的节点
void postorder(btnode* root);

//二叉树节点个数
int binarytreesize(btnode* root);
void binarytreesize_1(btnode* root, int size);
void binarytreesize_2(btnode* root, int* psize);

//二叉树叶子结点个数
int binarytreeleafsize(btnode* root);

//二叉树第k层节点个数
int binarytreelevelksize(btnode* root, int k);

//二叉树的深度/高度
int binarytreedepth(btnode* root);

//二叉树查找值为x的节点
btnode* binarytreefind(btnode* root, btdatatype x);

//二叉树的销毁
void  binarytreedestroy(btnode* root);

//层序遍历
void levelorder(btnode* root);

//判断是否为完全二叉树
bool binarytreecomplete(btnode* root);

//binarytree.c
#define  _CRT_SECURE_NO_WARNINGS 1

#include"binarytree.h"

//建立新的树节点
btnode* buynode(btdatatype x)
{
	btnode* newnode = (btnode*)malloc(sizeof(btnode));
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;
}

//前序遍历树的节点
void preorder(btnode* root)
{
	//递归的终止条件：遍历到空节点
	if (root == NULL)
	{
		return;
	}
	//先访问根节点
	printf("%c ", root->data);
	//再遍历左子树
	preorder(root->left);
	//再遍历右子树
	preorder(root->right);
}

//中序遍历树的节点
void inorder(btnode* root)
{
	if (root == NULL)
	{
		return;
	}
	//先遍历左子树
	inorder(root->left);
	//再访问根节点
	printf("%c ", root->data);
	//再遍历右子树
	inorder(root->right);
}

//后序遍历树的节点
void postorder(btnode* root)
{
	if (root == NULL)
	{
		return;
	}
	//先遍历左子树
	postorder(root->left);
	//再遍历右子树
	postorder(root->right);
	//最后访问根节点
	printf("%c ", root->data);
}

//二叉树节点个数
void binarytreesize_1(btnode* root, int size)
{
	if (root == NULL)
	{
		return;
	}
	size++;
	binarytreesize_1(root->left, size);
	binarytreesize_1(root->right, size);
}

void binarytreesize_2(btnode* root, int* psize)
{
	if (root == NULL)
	{
		return;
	}
	(*psize)++;
	binarytreesize_2(root->left, psize);
	binarytreesize_2(root->right, psize);
}

int binarytreesize(btnode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return 1 + binarytreesize(root->left) + binarytreesize(root->right);
}

//二叉树叶子结点个数
int binarytreeleafsize(btnode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return binarytreeleafsize(root->left) + binarytreeleafsize(root->right);
}

//二叉树第k层节点个数
int binarytreelevelksize(btnode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)//树的根在第一层
	{
		return 1;
	}
	return binarytreelevelksize(root->left, k - 1) + binarytreelevelksize(root->right, k - 1);
}

//二叉树的深度/高度
int binarytreedepth(btnode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftlen = binarytreedepth(root->left);
	int rightlen = binarytreedepth(root->right);
	return 1 + (leftlen > rightlen ? leftlen : rightlen);
}

//二叉树查找值为x的节点
btnode* binarytreefind(btnode* root, btdatatype x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	//如果在左子树中找到了，就不用在右子树中找了
	btnode* leftfind = binarytreefind(root->left, x);
	if (leftfind)
	{
		return leftfind;
	}
	//说明左子树中没有找到
	//再到右子树中继续找
	btnode* rightfind = binarytreefind(root->right, x);
	if (rightfind)
	{
		return rightfind;
	}
	//说明右子树中也没有找到
	return NULL;
}

//二叉树的销毁
//二叉树的销毁:要销毁二叉树，肯定是要先遍历二叉树，那么我们应该如何遍历二叉树呢？
//可以参考已有的遍历方式：前序？中序？后序？
//前序和中序在遍历完子树前都会先遍历完根，先销毁根的话，就没办法再找到根的子树了，所以这两种遍历方式都不可取，我们只能后序遍历来销毁二叉树
void  binarytreedestroy(btnode** proot)
{
	if (*proot == NULL)
	{
		return;
	}
	binarytreedestroy(&((*proot)->left));
	binarytreedestroy(&((*proot)->right));
	free(*proot);
	*proot = NULL;
}
//
//层序遍历
void levelorder(btnode* root)
{
	if (root == NULL)
	{
		return;
	}
	//先创建一个队列
	Queue q;
	QueueInit(&q);
	//先让队头元素入队列
	QueuePush(&q, root);

	//不断循环直到队列为空
	while (!QueueEmpty(&q))
	{
		//先取队头元素
		btnode* top = QueueFront(&q);
		//出队
		QueuePop(&q);
		//访问队头元素
		printf("%c ", top->data);
		//如果左孩子不为空，左孩子入队
		if (top->left)
		{
			QueuePush(&q, top->left);
		}
		//如果右孩子不为空，右孩子入队
		if (top->right)
		{
			QueuePush(&q, top->right);
		}
	}
	QueueDesTroy(&q);
}


//判断是否为完全二叉树
bool binarytreecomplete(btnode* root)
{
	if (root == NULL)
	{
		return true;
	}
	//利用层序遍历的思想判断是否为完全二叉树
		//先创建一个队列
	Queue q;
	QueueInit(&q);
	//先让队头元素入队列
	QueuePush(&q, root);

	//不断循环直到队列为空
	while (!QueueEmpty(&q))
	{
		//先取队头元素
		btnode* top = QueueFront(&q);
		//出队
		QueuePop(&q);
		//如果队头元素为空，就直接跳出循环
		if (top == NULL)
		{
			break;
		}
	//走到这里，说明队列不为空，那么就让队头元素的左右孩子都入队列
		QueuePush(&q, top->left);
		QueuePush(&q, top->right);
	}

	//现在就只需要判断第一次得到空的队头元素后，剩下的元素是否是既有空节点又有非空节点（非完全二叉树）
	//如果剩下的元素只有空节点（完全二叉树）
	while (!QueueEmpty(&q))
	{
		//取队头元素
		btnode* top = QueueFront(&q);
		QueuePop(&q);
		if (top != NULL)
		{
			QueueDesTroy(&q);
			return false;
		}
	}
	QueueDesTroy(&q);
	return true;
}

//test.c
#define  _CRT_SECURE_NO_WARNINGS 1

#include"binarytree.h"

btnode* creattree()
{
	btnode* A = buynode('A');
	btnode* B = buynode('B');
	btnode* C = buynode('C');
	btnode* D = buynode('D');
	btnode* E = buynode('E');
	btnode* F = buynode('F');
	A->left = B;
	A->right = C;
	B->left = D;
	C->left = E;
	C->right = F;
	return A;
}

void test1()
{
	btnode* root=creattree();
	preorder(root);
}

void test2()
{
	btnode* root = creattree();
	inorder(root);
}

void test3()
{
	btnode* root = creattree();
	postorder(root);
}

void test4()
{
	btnode* root = creattree();
	int size = 0;
	binarytreesize_1(root, size);
	printf("树中的节点个数：%d\n", size);
}

void test5()
{
	btnode* root = creattree();
	int size = 0;
	binarytreesize_2(root, &size);
	printf("树中的节点个数：%d\n", size);
	binarytreesize_2(root, &size);
	printf("树中的节点个数：%d\n", size);
	binarytreesize_2(root, &size);
	printf("树中的节点个数：%d\n", size);
}

void test6()
{
	btnode* root = creattree();
	int size = binarytreesize(root);
	printf("树中的节点个数：%d\n", size);
	size = binarytreesize(root);
	printf("树中的节点个数：%d\n", size);
	size = binarytreesize(root);
	printf("树中的节点个数：%d\n", size);
}

void test7()
{
	btnode* root = creattree();
	int leafsize = binarytreeleafsize(root);
	printf("叶子结点的个数：%d\n", leafsize);
}
void test8()
{
	btnode* root = creattree();
	int levelksize = binarytreelevelksize(root,3);
	printf("第三层共有%d个节点\n", levelksize);
}

void test9()
{
	btnode* root = creattree();
	int depth= binarytreedepth(root);
	printf("树的深度：%d\n", depth);
}

void test10()
{
	btnode* root = creattree();
	btnode* find = binarytreefind(root, 'C');
	if (find)
	{
		printf("yes:%c\n", find->data);
	}
	else
	{
		printf("no\n");
	}
}

void test11()
{
	btnode* root = creattree();
	levelorder(root);
}

void test12()
{
	btnode* root = creattree();
	if (binarytreecomplete(root))
	{
		printf("是完全二叉树\n");
	}
	else
	{
		printf("不是完全二叉树\n");
	}
}
int main()
{
	//test1();
	//test2();
	//test3();
	//test4();
   //	test5();
	//test6();
	//test7();
	//test8();
	//test9();
	//test10();
	//test11();
	test12();
	return 0;
}

//queue.c
#define  _CRT_SECURE_NO_WARNINGS 1

#include"queue.h"

//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

//销毁
void QueueDesTroy(Queue* pq)
{
	QueueNode* pcur = pq->phead;
	while (pcur)
	{
		QueueNode* pnext = pcur->next;
		free(pcur);
		pcur = pnext;
	}
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

//入队列
//入队列是在队尾入的，所以入队列相当于链表的尾插
void QueuePush(Queue* pq, Qdatatype x)
{
	assert(pq);
	//申请新的节点空间
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	newnode->next = NULL;
	newnode->data = x;
	//尾插
	//如果此时队列中一个元素都没有
	if (pq->phead == NULL)
	{
		pq->phead = pq->ptail = newnode;
	}
	else//队列本来就有元素
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	(pq->size)++;
}

//判空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size == 0;
}

//出队列
//出队列是在队头出的，相当于链表的头删
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	//如果链表中只有一个元素
	if (pq->phead->next == NULL)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
	}
	else//直接头删
	{
		QueueNode* newhead = pq->phead->next;
		free(pq->phead);
		pq->phead = newhead;
	}
	(pq->size)--;
}

//取队头数据
Qdatatype QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}


//取队尾数据
Qdatatype QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}

//队列有效元素个数
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

//queue.h
#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

//队列的结构
//先定义队列中节点的结构——队列的底层是链表
typedef struct btnode* Qdatatype;

typedef struct QueueNode
{
	Qdatatype data;
	struct QueueNode* next;
}QueueNode;

//队列的结构定义：
typedef struct Queue
{
	QueueNode* phead;//队头
	QueueNode* ptail;//队尾
	int size;//队列中有效数据个数
}Queue;

//初始化
void QueueInit(Queue* pq);
//销毁
void QueueDesTroy(Queue* pq);

//入队列
void QueuePush(Queue* pq, Qdatatype x);
//出队列
void QueuePop(Queue* pq);
//取队头数据
Qdatatype QueueFront(Queue* pq);
//取队尾数据
Qdatatype QueueBack(Queue* pq);
//判空
bool QueueEmpty(Queue* pq);
//队列有效元素个数
int QueueSize(Queue* pq);