线性代数·概念特性 | 正交向量组 / 正交基 / 标准正交基 / 单位矩阵 / 正交矩阵 / 正交变换

注：本文为 “线性代数 ” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未整理去重。
如有内容异常，请看原文。

【机器学习】【线性代数】正交基、标准正交基、正交矩阵、正交变换等数学知识点-CSDN博客

CV_ML_DP 于 2018-05-28 09:30:08 发布

摘要

本文详细介绍了正交向量、正交基、标准正交基等概念，阐述了正交矩阵及其特性，解释了正交变换的定义及应用，包括其对向量长度与夹角的影响，为线性代数在机器学习领域的应用提供了基础理论支撑。

1. 正交向量组

定义：设欧式空间 $V$ 中的一组非零向量 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k$，若对任意 $i\ne j$，都有内积 $({\alpha }_i,{\alpha }_j)=0$（即向量两两正交），则称该向量组为正交向量组。

正交向量组具有以下核心性质：

1. 正交向量组是线性无关的。
2. $n$ 维欧式空间中，两两正交的非零向量个数不会超过 $n$，即 $n$ 维欧式空间中一个正交向量组最多包含 $n$ 个向量。

2. 正交基

定义：在 $n$ 维欧式空间 $V$ 中，若一个正交向量组恰好包含 $n$ 个非零向量，则该正交向量组称为 $n$ 维欧式空间 $V$ 的正交基。

3. 标准正交基

定义：在 $n$ 维欧式空间 $V$ 中，若一个正交向量组满足两个条件——包含 $n$ 个向量、每个向量均为单位向量（即向量的模长 $\Vert {\alpha }_i\Vert =1$），则该正交向量组称为 $n$ 维欧式空间 $V$ 的标准正交基。

示例：3 维欧式空间 ${\mathbb{R}}^3$ 中，向量组 $\{(1,0,0),(0,1,0),(0,0,1)\}$ 是标准正交基，理由如下：

1. 向量两两正交：

   $(1,0,0)\cdot (0,1,0)=0$

   $(1,0,0)\cdot (0,0,1)=0$

   $(0,1,0)\cdot (0,0,1)=0$

2. 每个向量均为单位向量：

   $\Vert (1,0,0)\Vert =\sqrt{1^2+0^2+0^2}=1$，

   同理 $\Vert (0,1,0)\Vert =1$，$\Vert (0,0,1)\Vert =1$；

3. 向量个数等于空间维度（3 个）。

4. 单位矩阵

定义：若一个矩阵满足以下三个条件，则称该矩阵为单位矩阵，通常记作 $E$ 或 $I$：

1. 矩阵为方阵（即行数等于列数）；
2. 主对角线（从左上到右下的对角线）上的所有元素均为 1；
3. 除主对角线外，其余位置的元素均为 0。

示例：3 阶单位矩阵 $E_3$ 可表示为：
$$E_3=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

5. 正交矩阵

定义：若一个矩阵 $A$ 满足以下两个条件，则称该矩阵为正交矩阵：

1. 矩阵 $A$ 为方阵；
2. 矩阵 $A$ 与其转置矩阵 $A^T$ 的乘积等于单位矩阵 $E$，即 $A{A}^T=A^{T}A=E$。

若 $A$ 为正交矩阵，则其满足以下性质：

1. $A$ 的转置矩阵 $A^T$ 也是正交矩阵；
2. $A$ 的各行向量均为单位向量，且任意两个不同行向量正交；
3. $A$ 的各列向量均为单位向量，且任意两个不同列向量正交；
4. 对任意向量 $x,y\in {\mathbb{R}}^n$，均有内积关系 $(Ax,Ay)=(x,y)$；
5. 矩阵 $A$ 的行列式值为 $1$ 或 $-1$，即 $\det (A)=\pm 1$；
6. $A$ 的转置矩阵等于 $A$ 的逆矩阵，即 $A^T=A^{-1}$。

6. 正交变换

6.1 内积定义

对于欧式空间中的任意两个向量 $u$ 和 $v$，其內积定义为：
$$(u,v)=\Vert u\Vert \cdot \Vert v\Vert \cdot \cos ⟨u,v⟩$$
其中，$\Vert u\Vert$、$\Vert v\Vert$ 分别表示向量 $u$、$v$ 的模长，$⟨u,v⟩$ 表示向量 $u$ 与 $v$ 的夹角。

6.2 正交变换的定义

在 linear algebra 中，正交变换是线性变换的一种特殊形式：设 $V$ 为实内积空间，若线性变换 $T:V\to V$ 满足对任意 $u,v\in V$，均有 $(T(u),T(v))=(u,v)$（即变换前后向量的内积不变），则称 $T$ 为 $V$ 上的正交变换。

由于向量的模长（$\Vert u\Vert =\sqrt{(u,u)}$）与夹角（$\cos ⟨u,v⟩=\frac{(u,v)}{\Vert u\Vert \cdot \Vert v\Vert }$）均由内积定义，因此正交变换具有核心特性——变换前后，向量的模长和向量间的夹角均保持不变。

特别地：标准正交基经过正交变换后，仍为标准正交基。

6.3 欧式空间中正交变换的类型

欧式空间 $V$ 中的正交变换仅包含以下三类：

1. 旋转变换；
2. 反射变换；
3. 旋转与反射的组合变换（又称瑕旋转）。

6.4 正交变换的性质

设 $T$ 为欧式空间 $V$ 上的正交变换，$A,B$ 为正交矩阵，则 $T$ 满足以下性质：

1. 正交变换保持向量间的正交性：若 $u,v\in V$ 且 $(u,v)=0$，则 $(T(u),T(v))=0$；
2. 正交矩阵的乘积仍为正交矩阵：若 $A,B$ 均为正交矩阵，则 $AB$ 也为正交矩阵；
3. 正交矩阵的逆矩阵仍为正交矩阵：若 $A$ 为正交矩阵，则 $A^{-1}$ 也为正交矩阵；
4. 正交变换的逆运算易于实现：由于 $A^T=A^{-1}$，正交变换的逆变换可通过矩阵转置直接计算；
5. 内积不变性的推广：对任意 $u,v\in V$，$(T(u),T(v))=(u,v)$ 恒成立。

6.5 正交变换的示例与 Python 实现

设原矩阵 $A$、正交变换矩阵 $T$ 分别为：
$$A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right],T=\left[\begin{array}{ccc}2& 0& 0\\ 0& 3& 0\\ 0& 0& 4\end{array}\right]$$
则矩阵 $A$ 经过正交变换 $T$ 后得到的矩阵 $TA$ 为：
$$TA=\left[\begin{array}{ccc}2& 0& 0\\ 0& 3& 0\\ 0& 0& 4\end{array}\right]\cdot \left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]=\left[\begin{array}{ccc}2& 4& 6\\ 12& 15& 18\\ 28& 32& 36\end{array}\right]$$

Python 代码实现（基于 NumPy 库）

通过代码可直接定义原矩阵 $A$ 和变换矩阵 $T$，并计算变换后的矩阵 $TA$，代码如下：

import numpy as np

# 定义原矩阵 A
A = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])

# 定义正交变换矩阵 T
T = np.array([[2, 0, 0],
              [0, 3, 0],
              [0, 0, 4]])

# 计算 A 经过 T 变换后的矩阵 TA（矩阵乘法）
TA = np.dot(T, A)

# 输出结果
print("原矩阵 A:")
print(A)
print("\n正交变换矩阵 T:")
print(T)
print("\nA 经过 T 变换后的矩阵 TA:")
print(TA)

代码运行结果

原矩阵 A:
[[1 2 3]
 [4 5 6]
 [7 8 9]]

正交变换矩阵 T:
[[2 0 0]
 [0 3 0]
 [0 0 4]]

A 经过 T 变换后的矩阵 TA:
[[ 2  4  6]
 [12 15 18]
 [28 32 36]]

变换过程解读

由于变换矩阵 $T$ 是对角矩阵（仅主对角线有非零元素），该乘法等价于对 $A$ 的每行进行缩放：

• 主对角线元素 $2$：第 1 行所有元素 × 2

  将 $A$ 的第一行向量 $(1,2,3)$ 沿原方向 “拉伸” 2 倍，得到 $(2,4,6)$；

• 主对角线元素 $3$：第 2 行所有元素 × 3

  将 $A$ 的第二行向量 $(4,5,6)$ 沿原方向 “拉伸” 3 倍，得到 $(12,15,18)$；

• 主对角线元素 $4$：第 3 行所有元素 × 4

  将 $A$ 的第三行向量 $(7,8,9)$ 沿原方向 “拉伸” 4 倍，得到 $(28,32,36)$。

若 $T$ 主对角线上的元素为小于 1 的正数，则表示将 $A$ 中对应行向量“缩小”一定比例；

若 $T$ 主对角线以外的位置存在非零元素，则表示对 $A$ 进行特定方向的旋转操作。

上述概念在图象处理中具有重要应用，例如 OpenCV 中的几何变换功能，其核心原理就是通过变换矩阵与原图像矩阵的乘积，得到目标图像矩阵。

线性代数：正交基和标准正交基

倪桦 已于 2024-11-23 15:25:13 修改

描述一个空间有两种方式，一种是通过维度，另一种是通过空间的基。空间的基是一组向量，这组向量的个数即为空间的维度。

在一个 $n$ 维空间中，任意一组包含 $n$ 个线性无关向量的集合，都是该 $n$ 维空间的一组基。

一、二维空间的基示例

在二维空间中，最常见的基为单位向量组：

• $e_1=(1,0)$
• $e_2=(0,1)$
  

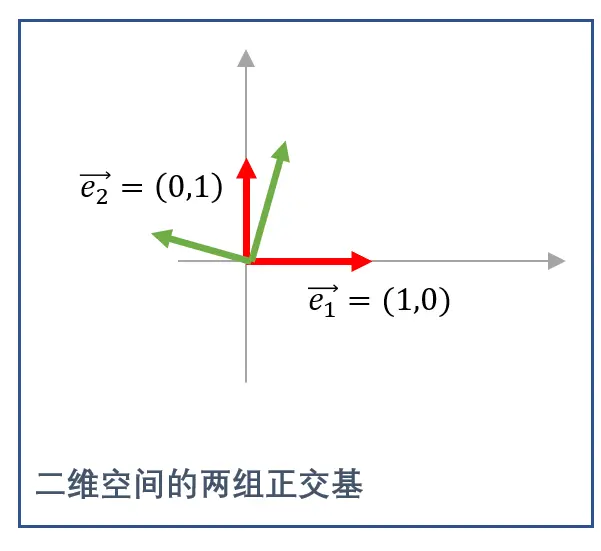
这组向量不仅是二维空间的基，也是后续将介绍的正交基与标准正交基。

二、正交的核心定义

为简化空间分析，我们通常优先选择互相垂直的向量组作为基，这类基称为正交基。

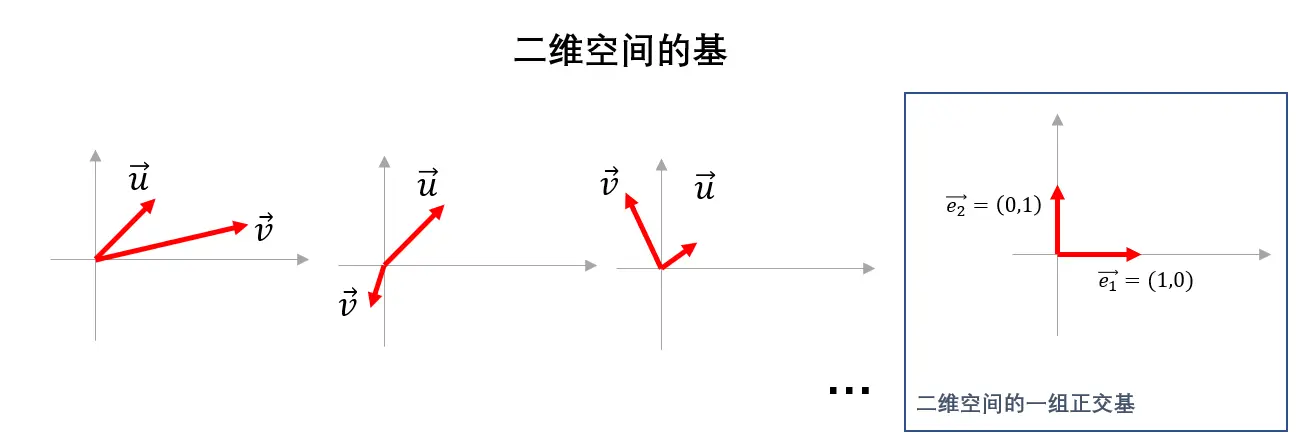
在数学研究中，为了便于描述空间中点的位置信息，通常会选择使用空间中一组互相垂直的向量构成的基，即 $正交基$。相较于非正交基，正交基在描述空间点的位置时更具优势，能够使计算过程更加简洁和直观。

要理解正交基，需先明确“正交”的数学定义：

1. 向量正交的定义

在欧几里得空间中，若两个向量互相垂直，则它们的点乘结果为 $0$。其数学表达式为：
$$\vec{u}\cdot \vec{v}=u_1\cdot v_1+u_2\cdot v_2+\cdots +u_n\cdot v_n=\Vert \vec{u}\Vert \cdot \Vert \vec{v}\Vert \cdot \cos \theta$$
其中：

• $\Vert \vec{u}\Vert$、$\Vert \vec{v}\Vert$ 分别表示向量 $\vec{u}$、$\vec{v}$ 的模（长度）；
• $\theta$ 表示两个向量的夹角。

当 $\theta =90^{\circ }$ 时，$\cos \theta =0$，此时 $\vec{u}\cdot \vec{v}=0$。因此，线性代数中“正交”的定义为：若两个向量的点乘结果为 $0$，则称这两个向量正交（互相垂直）。

2. 正交向量组的定义

若一组向量中任意两个向量均满足正交关系（点乘为 $0$），则称该向量组为正交向量组。

3. 正交向量组的重要性质：非零正交向量组必线性无关

• 零向量的特殊性：零向量与任意向量的点乘结果均为 $0$，即零向量与任意向量正交。但包含零向量的向量组一定线性相关（根据线性相关定义，零向量前的系数可取任意非零值，使线性组合为 $0$）。
• 非零正交向量组的线性无关性证明：
  设 $\overrightarrow{v_1},\overrightarrow{v_2},\dots ,\overrightarrow{v_p}$ 为一组非零正交向量组，若存在系数 $k_1,k_2,\dots ,k_p$ 满足：
  $$k_1\overrightarrow{v_1}+k_2\overrightarrow{v_2}+\cdots +k_p\overrightarrow{v_p}=0$$
  取向量组中的任意一个向量 $\overrightarrow{v_i}$，将其与等式两边同时点乘：
  $$(k_1\overrightarrow{v_1}+k_2\overrightarrow{v_2}+\cdots +k_p\overrightarrow{v_p})\cdot \overrightarrow{v_i}=0\cdot \overrightarrow{v_i}=0$$
  根据正交向量组的定义，$\overrightarrow{v_i}$ 与其他向量 $\overrightarrow{v_j}(j\ne i)$ 正交，即 $\overrightarrow{v_j}\cdot \overrightarrow{v_i}=0$，因此展开后仅保留 $\overrightarrow{v_i}\cdot \overrightarrow{v_i}$ 项：
  $$k_i\cdot (\overrightarrow{v_i}\cdot \overrightarrow{v_i})=0$$
  由于 $\overrightarrow{v_i}$ 是非零向量，其模的平方 $\Vert \overrightarrow{v_i}{\Vert }^2=\overrightarrow{v_i}\cdot \overrightarrow{v_i}>0$，因此 $k_i=0$。
  对所有 $i=1,2,\dots ,p$ 重复上述过程，可得到所有系数 $k_1=k_2=\cdots =k_p=0$，即该向量组仅存在零解，故非零正交向量组线性无关。

三、正交基的定义与性质

1. 正交基的定义

若某空间的一组基满足“两两正交”的条件，则称这组基为该空间的正交基。

2. 正交基的核心性质

根据前文结论，$n$ 维空间中任意 $n$ 个线性无关的向量均可作为该空间的基；而 $n$ 个非零正交向量组必线性无关，因此：
在 $n$ 维空间中，任意 $n$ 个非零正交向量构成的向量组，一定是该 $n$ 维空间的正交基。

（注：正交基中无需额外强调“排除零向量”，因为基的定义本身要求向量组线性无关，而包含零向量的向量组线性相关，无法成为基。）

四、标准正交基的定义

1. 标准正交基的定义

若某空间的一组正交基满足“所有向量的模均为 $1$”的条件，则称这组基为该空间的标准正交基（也称为“规范正交基”）。

例如，二维空间中的向量组 $\{(1,0),(0,1)\}$ 就是一组标准正交基：

• 两两正交：

  $(1,0)\cdot (0,1)=1\cdot 0+0\cdot 1=0$；

• 每个向量的模为 $1$：

  $\Vert (1,0)\Vert =\sqrt{1^2+0^2}=1$，

  $\Vert (0,1)\Vert =\sqrt{0^2+1^2}=1$。

2. 标准正交基的多样性

一个空间的标准正交基并非唯一。例如，在二维空间中，向量组 { ( cos ⁡ θ , sin ⁡ θ ) , ( − sin ⁡ θ , cos ⁡ θ ) } \left\{\left(\cos\theta, \sin\theta\right), \left(-\sin\theta, \cos\theta\right)\right\} {(cosθ,sinθ),(−sinθ,cosθ)}（其中 $\theta$ 为任意角度）也是一组标准正交基，只需验证：

• 两两正交：$\left(\cos \theta ,\sin \theta \right)\cdot \left(-\sin \theta ,\cos \theta \right)=-\cos \theta \sin \theta +\sin \theta \cos \theta =0$；
• 模为 $1$：$\Vert \left(\cos \theta ,\sin \theta \right)\Vert =\sqrt{{\cos }^2\theta +{\sin }^2\theta }=1$，同理另一向量的模也为 $1$。

因此，一个空间存在无数组标准正交基。

via：

• 【机器学习】【线性代数】正交基、标准正交基、正交矩阵，正交变换等数学知识点-CSDN博客
  https://blog.csdn.net/u012421852/article/details/80475497

• 线性代数：正交基和标准正交基-CSDN博客
  https://blog.csdn.net/Nh_code/article/details/143992386