3.【例3.1.1】一元线性回归

2.【例3.1.2】一元线性回归（续）

2.【例3.1.3】

前言

估计回归参数的最基本方法是最小二乘法。这个方法不仅仅在统计学中，就是在数学的其他分支，例如运筹学、计算数学、逼近论和控制论等，都是很重要的求解方法。本章前三节我们首先讨论如何应用最小二乘法求回归参数的最小二乘估计，并研究这种估计的基本性质。在本文四五部分，我们讨论了当有了一批实际数据后，如何考察导出最小二乘估计的基本假设的适用性以及当这些假设不适用时，对数据应该做的变换，即 $Box-Cox$ 变换。在本文第六部分我们讨论了广义最小二乘估计。在一些情况下，最小二乘估计并不是一个好的估计，于是统计学家提出了一些新的估计。在本文最后两部分，我们将讨论其中最重要的两种估计——岭估计和主成分估计。

一、经验线性回归方程

1.未知参数的估计

假设 $Y$ 为因变量， $X_{1},\cdots ,X_{p-1}$ 为对 $Y$ 有影响的 $p-1$ 个自变量，并且他们之间具有线性关系 $Y=\beta _{0}+\beta _{1}X_{1}+\cdots+\beta _{p-1}X_{p-1}+e(3.1.1)$ ，其中 $e$ 为误差项，它表示除了 $X_{1},\cdots ,X_{p-1}$ 之外其他因素对 $Y$ 的影响以及试验或测量误差。 $\beta _{0},\beta _{1},\cdots,\beta _{p-1}$ 是待估计的未知参数。

假设我们有了因变量 $Y$ 和自变量 $X_{1},\cdots ,X_{p-1}$ 的 $n$ 组观测值：

$(x_{i1},\cdots,x_{i,p-1},y_{i}),i=1,\cdots,n$

他们满足 $y_{i}=\beta _{0}+x_{i1}\beta _{1}+\cdots+x_{i,p-1}\beta _{p-1}+e_{i},i=1,\cdots,n(3.1.2)$ 。误差项 $e_{i},i=1,\cdots,n$ 满足如下假设（ ${\color{Red} Gauss-MarKov}$ 假设 ${\color{Red} (3.1.3)}$ ）：

$E(e_{i})=0$
$Var(e_{i})=\sigma ^2$ （等方差）
$Cov(e_{i},e_{j})=0,i\neq j$ （不相关）

若用矩阵形式， $(3.1.2)$ 变形为：

$\begin{pmatrix} y_{1}\\ y_{2}\\ \vdots \\ y_{n} \end{pmatrix}=\begin{pmatrix} 1 &x_{11} &\cdots &x_{1,p-1} \\ 1& x_{21}& \cdots &x_{2,p-1}\\ \vdots & \vdots & &\vdots \\ 1& x_{41} &\cdots &x_{n,p-1} \end{pmatrix}\begin{pmatrix} \beta _{0}\\ \beta _{1}\\ \vdots \\ \beta _{p-1} \end{pmatrix}+\begin{pmatrix} e_{1}\\ e_{2}\\ \vdots\\ e_{n} \end{pmatrix}$

等价地， $y=X\beta +e,(3.1.4)$ 。 $y$ 是 $n*1$ 的变量观测向量， $X$ 为 $n*p$ 的已知设计矩阵， $\beta$ 为 $p*1$ 未知参数向量， $e$ 为随机误差向量。用矩阵形式可将 ${\color{Red} Gauss-MarKov}$ 假设 ${\color{Red} (3.1.3)}$ 写成：

$E(e)=0,Cov(e)=\sigma ^2I_{n}.(3.1.5)$

将 $(3.1.4),(3.1.5)$ 合并在一起，就得到最基本、最重要的线性回归模型：

${\color{Red} y=X\beta +e,E(e)=0,Cov(e)=\sigma ^2 I_{n}.(3.1.6)}$

获得参数向量 $\beta$ 的估计的一个最重要的方法是最小二乘法，这个方法是找 $\beta$ 的估计，使得偏差向量 $e=y-X\beta$ 的长度之平方 $\left \| y-X\beta \right \|^2$ 达到最小。记

$Q(\beta )=\left \| y-X\beta \right \|^2=(y-X\beta)^{'}(y-X\beta)=(y^{'}-\beta ^{'}X^{'})(y-X\beta)=y^{'}y-y^{'}X\beta-\beta^{'}X^{'}y+\beta^{'}X^{'}X\beta=y^{'}y-2y^{'}X\beta+\beta^{'}X^{'}X\beta$

对 $\beta$ 求偏导，并命其为0，即

$\frac{\partial Q(\beta)}{\partial \beta }=0-X^{'}y-X^{'}y+2X^{'}X\beta=2X^{'}X\beta-2X^{'}y=0\Rightarrow X^{'}X\beta=X^{'}y$

称 ${\color{Red} X^{'}X\beta=X^{'}y(3.1.7)}$ 为正则方程。这个线性方程组有唯一解的充要条件是 $X^{'}X$ 的秩为 $p$ 。等价地， $X$ 的秩为 $p$ 。以后，在线性回归模型的讨论中，我们总假定这个条件满足。于是，我们得到 $(3.1.7)$ 的唯一解 ${\color{Red} \hat{\beta }=(X^{'}X)^{-1}X^{'}y.(3.1.8)}$ 。

根据微积分的极值理论， $\hat{\beta }$ 只是函数 $Q(\beta )$ 的一个驻点。我们还需要证明， $\hat{\beta }$ 确实使 $Q(\beta )$ 达到最小。事实上，对任意一个 $\beta$ ，有：

$\left \| y-X\beta \right \|^2=\left \| y-X\hat{\beta }+X(\hat{\beta }-\beta ) \right \|^2=(y-X\hat{\beta }+X\hat{\beta }-X\beta )^{'}(y-X\hat{\beta }+X\hat{\beta }-X\beta )=[(y-X\hat{\beta })^{'}+(X\hat{\beta }-X\beta) ^{'}][(y-X\hat{\beta })+(X\hat{\beta }-X\beta) ]=\left \| y-X\hat{\beta }\right \|^2+(y-X\hat{\beta })^{'}X(\hat{\beta}-\beta)+(\hat{\beta}-\beta)^{'}X^{'}(y-X\hat{\beta })+(\hat{\beta}-\beta)^{'}X^{'}X(\hat{\beta}-\beta)=\left \| y-X\hat{\beta }\right \|^2+(\hat{\beta}-\beta)^{'}X^{'}X(\hat{\beta}-\beta)+2(\hat{\beta}-\beta)^{'}X^{'}(y-X\hat{\beta })$

因为 $\hat{\beta }$ 满足正则方程 $(3.1.7)$ ，于是 $X^{'}(y-X\hat{\beta })=0$ ，因而上式第三项为0，这就证明了对任意的 $\beta$ ，有

$\left \| y-X\beta \right \|^2=\left \| y-X\hat{\beta } \right \|^2+(\hat{\beta }-\beta )^{'}X^{'}X(\hat{\beta }-\beta )$

又因为 $X^{'}X$ 是一个正定矩阵，故上式第二项总是非负的，于是

$Q(\beta )=\left \| y-X\beta \right \|^2\geqslant \left \| y-X\hat{\beta } \right \|^2=Q(\hat{\beta })$

且等号成立当且仅当

$(\hat{\beta }-\beta )^{'}X^{'}X(\hat{\beta }-\beta )=0.$

2.经验线性回归方程

记 $\hat{\beta }=(\hat{\beta _{0}},\hat{\beta _{1}},\cdots,\hat{\beta _{p-1}})^{'}$ ，并将其带入 $(3.1.1)$ 。去掉误差项，得到

$\hat{Y}=\hat{\beta _{0}}+\hat{\beta _{1}}X_{1}+\cdots+\hat{\beta _{p-1}}X_{p-1}(3.1.11)$

称为经验线性回归方程。这个方程是不是描述了 $Y$ 与自变量 $X_{1},\cdots,X_{p-1}$ 的真实关系，还需要做进一步的统计分析。

3.【例3.1.1】一元线性回归

假设影响因变量 $Y$ 的因素只有一个，记为 $X$ 。现在我们对 $Y,X$ 获得了 $n$ 次观测

$(y_{i},x_{i}),i=1,2,\cdots,n$

于是我们有 $y_{i}=\alpha +\beta x_{i}+e_{i},i=1,2,\cdots,n$ ，这时正则方程 $X^{'}X\beta =X^{'}y(3.1.7)$ 变为：

$\begin{pmatrix} 1 &\cdots &1 \\ x_{1}& \cdots & x_{n} \end{pmatrix}\begin{pmatrix} 1 & x_{1}\\ \vdots &\vdots \\ 1 & x_{n} \end{pmatrix}\begin{pmatrix} \alpha \\ \beta \end{pmatrix}={\color{Red} \begin{pmatrix} n &\Sigma x_{i}\\ \Sigma x_{i} & \Sigma x_{i}^2 \end{pmatrix}\begin{pmatrix} \alpha \\ \beta \end{pmatrix}=\begin{pmatrix} \Sigma y_{i}\\ \Sigma x_{i}y_{i} \end{pmatrix}}=\begin{pmatrix} 1 &\cdots &1 \\ x_{1}& \cdots & x_{n} \end{pmatrix}\begin{pmatrix} y_{1}\\ \vdots \\ y_{n} \end{pmatrix}$

当 $x_{i},i=1,\cdots,n$ 不全相等时， $\sum_{i}(x_{i}-\bar{x})^2\neq 0$ ，这里 $\bar{x}=\frac{\Sigma x_{i}}{n}$ 。于是正则方程左端的系数行列式 $=n\Sigma (x_{i}-\bar{x})^2=n\Sigma x_{i}^2-(\Sigma x_{i})^2\neq 0$ 。经过初等计算可以解得 $\alpha ,\beta$ 的最小二乘估计为

$\hat{\alpha }=\bar{y}-\hat{\beta }\bar{x}$

$\hat{\beta }=\frac{\Sigma x_{i}y_{i}-n\bar{x}\bar{y}}{\Sigma x_{i}^2 -n\bar{x}^2}$

其中， $\bar{y}=\frac{\Sigma y_{i}}{n}$ 。

二、中心化的经验线性回归方程

1.中心化

在回归分析的应用中，我们常常要把原始观测数据进行中心化和标准化，这对于我们的统计分析将是有益的。记 $\bar{x_{j}}=\frac{1}{n}\sum_{i=1}^{n}x_{ij},j=1,\cdots,p-1$ 为第 $j$ 个回归自变量 $n$ 次取值的平均值。将 $(3.1.2)$ 改写为

$y_{i}=\alpha +(x_{i1}-\bar{x_{1}})\beta _{1}+\cdots+(x_{i,p-1}-\bar{x_{p-1}})\beta _{p-1}+e_{i},i=1,\cdots,n.(3.1.13)$

这里 $\alpha$ 与 $(3.1.2)$ 中的 $\beta _{0}$ 有如下关系：

$\alpha =\beta _{0}+\bar{x_{1}}\beta _{1}+\cdots+\bar{x_{p-1}}\beta _{p-1}$

在 $(3.1.13)$ 中，我们把每个回归自变量减去了他们的平均值，这称为中心化。若记

$X_{c}=\begin{pmatrix} x_{11}-\bar{x_{1}} & x_{12}-\bar{x_{2}} & \cdots &x_{1,p-1}-\bar{x_{p-1}} \\ x_{21}-\bar{x_{1}} & x_{22}-\bar{x_{2}} & \cdots &x_{2,p-1}-\bar{x_{p-1}} \\ \vdots & \vdots & & \\ x_{n1}-\bar{x_{1}} & x_{n2}-\bar{x_{2}} &\cdots & x_{n,p-1}-\bar{x_{p-1}} \end{pmatrix}(3.1.14)$

则 $(3.1.13)$ 可改写为

$y=X\beta +e=\begin{pmatrix} 1_{n} & X_{c} \end{pmatrix}\begin{pmatrix} \alpha \\ \beta \end{pmatrix}+e=\alpha 1_{n}+X_{c}\beta +e.(3.1.15)$

这里 $1_{n}$ 表示所有分量皆为1的 $n*1$ 向量。 $\beta ^{'}=\left ( \beta _{1},\cdots, \beta _{p-1}\right )$ 称为回归系数。这个模型跟前面模型不同之处是：我们把回归常数项 $\alpha$ 与回归系数 $\beta$ 分离开来了，且设计矩阵 $X_{c}$ 已经中心化，它满足：

$1^{'}X_{c}=0,(3.1.16)$

也就是 $X_{c}$ 每个列向量的 $n$ 个元素之和等于0.由于此性质，正则方程 $(3.1.7)$ 变形为：

$X^{'}X\beta =X^{'}y\Rightarrow \begin{pmatrix} 1_{n}& X_{c} \end{pmatrix}^{'}\begin{pmatrix} 1_{n}& X_{c} \end{pmatrix}\begin{pmatrix} \alpha \\ \beta \end{pmatrix}=\begin{pmatrix} 1_{n}^{'}\\ X_{c}^{'} \end{pmatrix}\begin{pmatrix} 1_{n}& X_{c} \end{pmatrix}\begin{pmatrix} \alpha \\ \beta \end{pmatrix}={\color{Red} \begin{pmatrix} n &0 \\ 0& X_{c}^{'}X_{c} \end{pmatrix}\begin{pmatrix} \alpha \\ \beta \end{pmatrix}=\begin{pmatrix} 1^{'}y\\ X_{c}^{'}y \end{pmatrix}}=\begin{pmatrix} 1_{n}^{'}\\ X_{c}^{'} \end{pmatrix}y=X^{'}y$

等价地，

$\left\{\begin{matrix} n\alpha =1^{'}y\\ X_{c}^{'}X_{c}\beta =X_{c}^{'}y \end{matrix}\right.(3.1.18)$

于是回归参数的最小二乘估计为：

$\left\{\begin{matrix} \hat{\alpha }=\bar{y}\\ \hat{\beta }=(X_{c}^{'}X_{c})^{-1}X_{c}^{-1}y \end{matrix}\right.(3.1.19)$

这样，对经过中心化程序的线性回归模型 $(3.1.13)$ ，回归常数项的最小二乘估计总是等于因变量的观测平均值，而 $\beta$ 的最小二乘估计 $\hat{\beta }=(X_{c}^{'}X_{c})^{-1}X_{c}^{'}y$ 将相当于从线性回归模型 $y=X_{c}\beta +e$ ，按原来的最小二乘估计公式 $(3.1.8)$ 计算得到的。于是，我们就把常数项和回归系数的估计也分离开了。因为在实际应用中，我们总是特别关心回归系数，所以中心化是很必要的。

2.【例3.1.2】一元线性回归（续）

将例3.1.1所研究的一元线性回归模型进行中心化，得到

$y_{i}=\alpha +(x_{i}-\bar{x})\beta +e_{i},i=1,\cdots,n.(3.1.20)$

根据 $(3.1.18)$ ，我们可以得到 $\alpha ,\beta$ 的最小二乘估计：

$\left\{\begin{matrix} \hat{\alpha }=\bar{y}\\ \hat{\beta }=\frac{\sum_{i}y_{i}(x_{i}-\bar{x})}{\sum_{i}(x_{i}-\bar{x})^2} \end{matrix}\right..$

三、标准化的经验线性回归方程

1.标准化

除了中心化，对自变量经常做的另一种处理叫做标准化。记

$s_{j}^2=\sum_{i=1}^{n}(x_{ij}-\bar{x_{j}})^2,j=1,\cdots,p-1$

$z_{ij}=\frac{x_{ij}-\bar{x_{j}}}{s_{j}}.(3.1.21)$

我们刚才讨论过，将 $x_{ij}$ 减去 $\bar{x_{j}}$ 称为中心化，现在再除以 $s_{j}$ ，这称为标准化。命 $Z=(z_{ij})$ ，则 $Z$ 就是将原来的设计矩阵 $X$ 经过中心化和标准化得到的新设计矩阵，这个矩阵具有如下性质：

$(a)1^{'}Z=0$
$(b)R= ^{d}Z^{'}Z=(r_{ij})$

$r_{ij}=\frac{\sum_{k=1}^{n}(x_{ki}-\bar{x_{i}})(x_{kj}-\bar{x_{j}})}{s_{i}s_{j}},i,j=1,\cdots,p-1.(3.1.22)$

性质 $(a)$ 是中心化的作用，它使设计阵每列之和都为0；性质 $(b)$ 是中心化后再施以标准化后的结果。如果把回归自变量都看成随机向量， $X$ 的第 $j$ 列为第 $j$ 个自变量的 $n$ 个随机样本，那么 $R=Z^{'}Z$ 的第 $(i.j)$ 元正是回归自变量 $X_{i}$ 与 $X_{j}$ 的样本相关系数，因而 $R$ 是回归自变量的相关阵，于是 $r_{ii}=1$ 对一切 $i$ 成立。

这样做的好处有两条。其一，用 $R$ 可以分析回归自变量之间的相关关系；其次，在一些问题中，诸回归自变量所用的单位可能不相同，取值范围大小也不同，经过标准化，消去了单位和取值范围的差异，这便于对回归系数估计值的统计分析。

需要注意，如果把模型 $(3.1.2)$ 既经过中心化，又经过标准化，则变形为

$y_{i}=\alpha +\left ( \frac{x_{i1}-\bar{x_{1}}}{s_{1}} \right )\beta _{1}+\cdots+\left ( \frac{x_{i,p-1}-\bar{x_{p-1}}}{s_{p-1}} \right )\beta _{p-1}+e_{i}.(3.1.23)$

这里的 $\alpha$ 和前面的 $\alpha$ 当然不同，但我们没有必要写出它和 $\beta _{0}$ 的关系，用矩阵形式，模型 $(3.1.23)$ 就是：

$y=\alpha 1+Z\beta +e$

当我们对这个模型求到了参数的最小二乘估计： $\hat{\alpha }=\bar{y},\hat{\beta _{1}},\cdots,\hat{\beta _{p-1}}$ 之后，所对应的经验回归方程应为

$\hat{Y}=\hat{\alpha }+\left ( \frac{X_{1}-\bar{x_{1}}}{s_{1}} \right )\hat{\beta _{1}}+\cdots+\left ( \frac{X_{p-1}-\bar{x_{p-1}}}{s_{p-1}} \right )\hat{\beta _{p-1}}=\left ( \hat{\alpha }-\sum_{i=1}^{p-1} \frac{\bar{x_{i}}}{s_{i}}\hat{\beta _{i}}\right )+\sum_{i=1}^{p-1}\left ( \frac{\hat{\beta _{i}}}{s_{i}} \right )X_{i}.(3.1.24)$

2.【例3.1.3】

一个试验容器靠蒸汽供应能量，使其保持恒温。表3.1.1中，自变量 $X$ 表示容器周围空气单位时间的平均温度， $Y$ 表示单位时间内消耗的蒸汽量（L），共观测了25个单位时间。图3.1.1是这些数据的散点图。

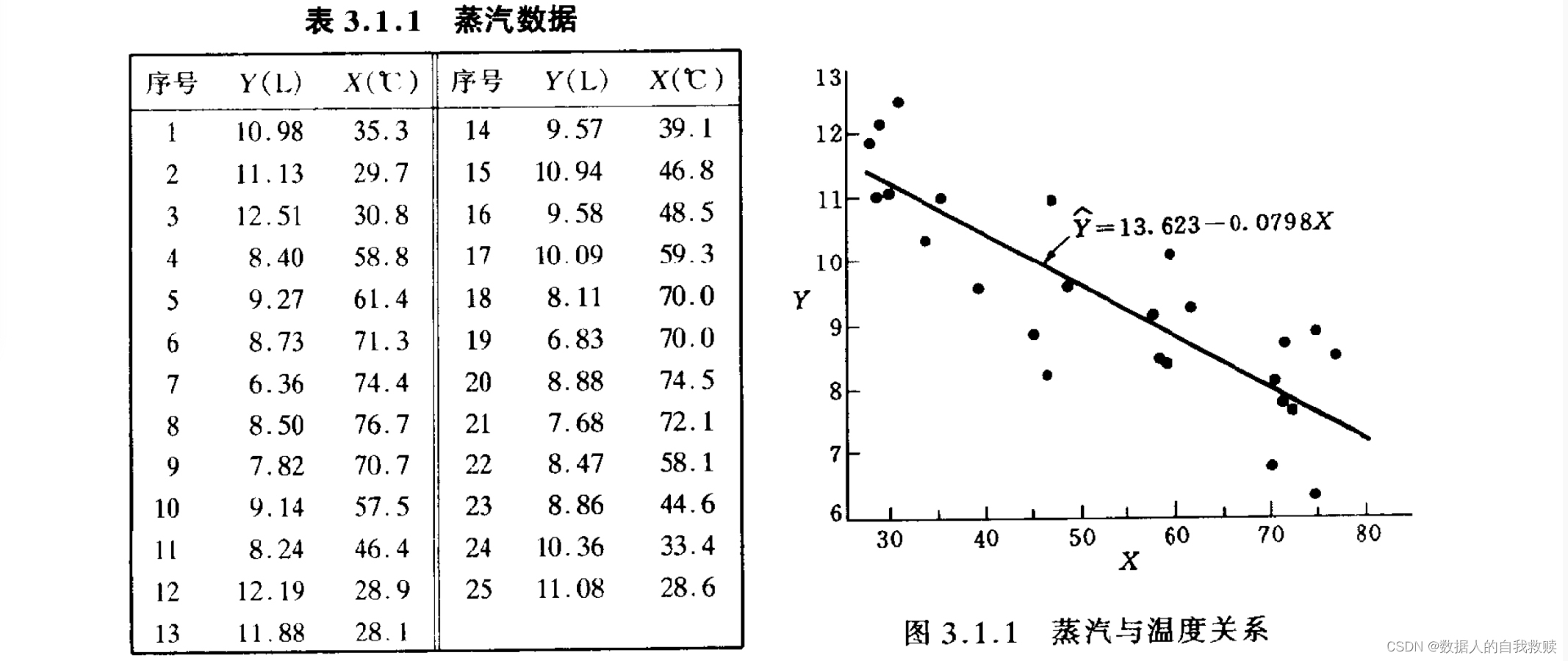
对这组数据，应用中心化线性回归模型 $(3.1.20)$ ，我们得到 $\left\{\begin{matrix} \bar{y}=9.424\\ \bar{x}=52.60 \end{matrix}\right.$ 。常数项 $\alpha$ 和回归系数 $\beta$ 的最小二乘估计分别为 $\left\{\begin{matrix} \hat{\alpha }=\bar{y}=9.424,\\ \hat{\beta }=-0.0798. \end{matrix}\right.$ 。于是经验回归方程为

$\hat{Y}=9.424-0.0798(X-52.60)\Rightarrow \hat{Y}=13.623-0.0798X$

从这个经验回归方程，我们看到，周围环境的温度每上升1摄氏度保持容器恒温在单位时间内所需要的蒸汽量减少0.0978（L）。一般来说，一个经验回归方程是不是真正描述了因变量和自变量之间的关系，最重要的应该是根据实践来检验，从问题本身专业知识的角度来分析。当然，从数理统计的角度也有一些辅助方法，这将在下一章讨论。

本文含有隐藏内容，请开通VIP 后查看

【应用回归分析】CH3 回归参数的估计1——最小二乘估计

前言

一、经验线性回归方程

1.未知参数的估计

2.经验线性回归方程

3.【例3.1.1】一元线性回归

二、中心化的经验线性回归方程

1.中心化

2.【例3.1.2】一元线性回归（续）

三、标准化的经验线性回归方程

1.标准化

2.【例3.1.3】

网站公告

今日签到

热门文章

最新发布