数据结构 【树状数组】【线段树】【珂朵莉树】

一.区间合并

1.AcWing245你能回答这些问题吗

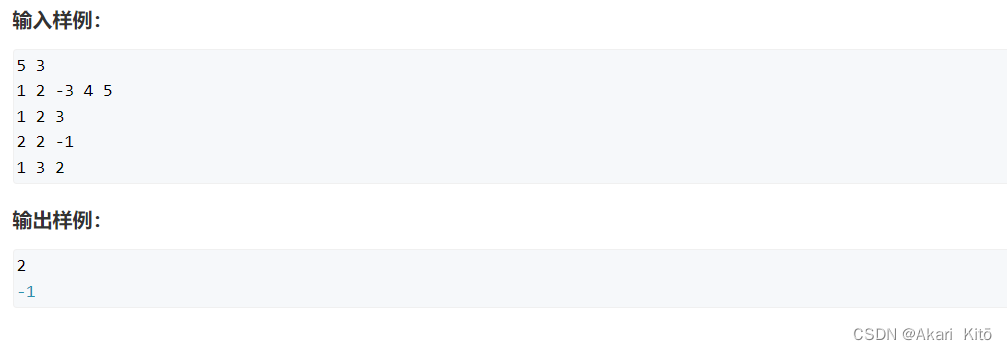
分析：

线段树。维护四个变量，即可实现区间合并。

mx 区间最大连续子段和

mx_l 以区间左端点为左界的最大连续字段和

mx_r 以区间左端点为左界的最大连续字段和

sum 区间和

AC代码:

#include <bits/stdc++.h>

using namespace std;

const int inf = 0x3f3f3f3f;
int n, m;
int ar[500050];
struct node
{
    int l, r;
    int mx, mx_l, mx_r, sum;
}tree[2000050];
int op, x, y;

void pushup(node &a, node &b, node &c)
{
    a.mx = max(max(b.mx, c.mx), b.mx_r + c.mx_l);
    a.mx_l = max(b.mx_l, b.sum + c.mx_l);
    a.mx_r = max(c.mx_r, c.sum + b.mx_r);
    a.sum = b.sum + c.sum;
}

void build(int p, int l, int r)
{
    tree[p].l = l, tree[p].r = r;

    if(l == r)
    {
        tree[p].mx = tree[p].mx_l = tree[p].mx_r = tree[p].sum = ar[l];
        return ;
    }
    int mid = (l + r) >> 1;
    build(p<<1, l, mid);
    build(p<<1|1, mid + 1, r);
    pushup(tree[p], tree[p<<1], tree[p<<1|1]);
}

node query(int p, int l, int r)
{
    if(l <= tree[p].l && tree[p].r <= r) return tree[p];

    int mid = (tree[p].l + tree[p].r) >> 1;
    if(r <= mid) return query(p<<1, l, r);
    else if(l > mid) return query(p<<1|1, l, r);
    else
    {
        node left = query(p<<1, l, r);
        node right = query(p<<1|1, l, r);
        node res;
        pushup(res, left, right);
        return res;
    }
}

void updata(int p, int x, int y)
{
    if(tree[p].l == tree[p].r) tree[p].mx = tree[p].mx_l = tree[p].mx_r = tree[p].sum = y;
    else
    {
        int mid = (tree[p].l + tree[p].r) >> 1;
        if(mid >= x) updata(p<<1, x, y);
        else updata(p<<1|1, x, y);
        pushup(tree[p], tree[p<<1], tree[p<<1|1]);
    }
}

int main()
{
    scanf("%d%d", &n, &m);

    for(int i = 1; i <= n; ++i) scanf("%d", &ar[i]);

    build(1, 1, n);

    while(m--)
    {
        scanf("%d%d%d", &op, &x, &y);
        if(op == 1)
        {
            if(x > y) swap(x, y);
            printf("%d\n", query(1, x, y).mx);
        }
        else updata(1, x, y);
    }

    return 0;
}

2.Codeforces Round #742 (Div. 2) E. Non-Decreasing Dilemma

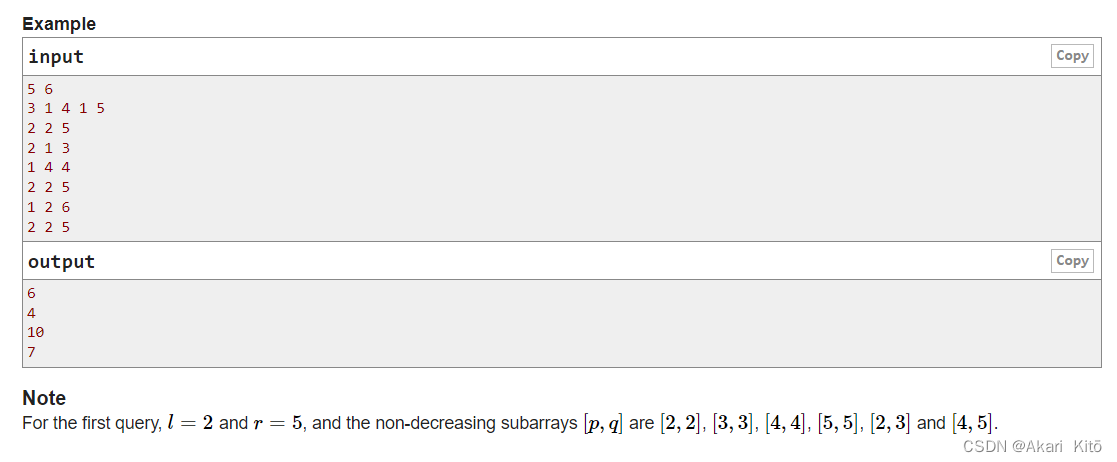
题意：

长度为n的数组，q次询问，每次询问三个参数op,x,y

op==1,ar[x]=y;

op==2,查询区间内有多少个不降的子数组。

分析：

同上一个题一样，除了维护询问的属性sum以外,再维护子数组左右边界分别为区间边界时最长的长度len_l,len_r,，以及区间长度len,即可实现区间合并。

AC代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
int n, q;
ll ar[200050];
struct node
{
    int l, r;
    ll len_l, len_r, sum, len;

//    void print()
//    {
//        cout << l << ' ' << r << ' ' << len_l << ' ' << len_r << ' ' << sum << ' ' << len << '\n';
//    }
}tree[800050];
int op;
ll x, y;

ll calc(ll n)
{
    return (1ll + n) * n / 2ll;
}

void pushup(node &p, node &le, node &ri)
{
    p.l = le.l;
    p.r = ri.r;
    if(ar[le.r] <= ar[ri.l])
    {
        p.sum = le.sum + ri.sum - calc(le.len_r) - calc(ri.len_l) + calc(le.len_r + ri.len_l);

        if(le.len == le.len_l) p.len_l = le.len + ri.len_l;
        else p.len_l = le.len_l;

        if(ri.len_r == ri.len) p.len_r = ri.len + le.len_r;
        else p.len_r = ri.len_r;

        p.len = le.len + ri.len;
    }
    else
    {
        p.sum = le.sum + ri.sum;
        p.len_l = le.len_l;
        p.len_r = ri.len_r;
        p.len = le.len + ri.len;
    }
}

void pushup(int p)
{
    pushup(tree[p], tree[p<<1], tree[p<<1|1]);
}

void build(int p, int l, int r)
{
    tree[p].l = l, tree[p].r = r;

    if(l == r)
    {
        tree[p].len_l = tree[p].len_r = tree[p].sum = tree[p].len = 1;
        return ;
    }

    int mid = (l + r) >> 1;
    build(p<<1, l, mid);
    build(p<<1|1, mid + 1, r);
    pushup(p);
}

void updata(int p, int pos, ll y)
{
    if(tree[p].l == tree[p].r) ar[pos] = y;
    else
    {
        int mid = (tree[p].l + tree[p].r) >> 1;
        if(mid >= x) updata(p<<1, pos, y);
        else updata(p<<1|1, pos, y);
        pushup(p);
    }
}

node query(int p, int l, int r)
{
    if(l <= tree[p].l && tree[p].r <= r)
    {
        //tree[p].print();
        return tree[p];
    }

    int mid = (tree[p].l + tree[p].r) >> 1;
    if(r <= mid) return query(p<<1, l, r);
    else if(l > mid) return query(p<<1|1, l, r);
    else
    {
        node res;
        node left = query(p<<1, l, r);
        node right = query(p<<1|1, l, r);
        pushup(res, left, right);
        //res.print();
        return res;
    }

}

int main()
{
    cin >> n >> q;
    for(int i = 1; i <= n; ++i) cin >> ar[i];

    build(1, 1, n);

//    for(int i = 1; i <= n * 4; ++i)
//    {
//        cout << i << ' ' ;
//        tree[i].print();
//    }

    while(q--)
    {
        cin >> op >> x >> y;
        if(op == 1) updata(1, x, y);
        else
        {
            //query(1, x, y).print();
            cout << query(1, x, y).sum << '\n';
        }
    }
    return 0;
}

二.珂朵莉树

牛客练习赛100 E 小红的公倍数(珂朵莉树)

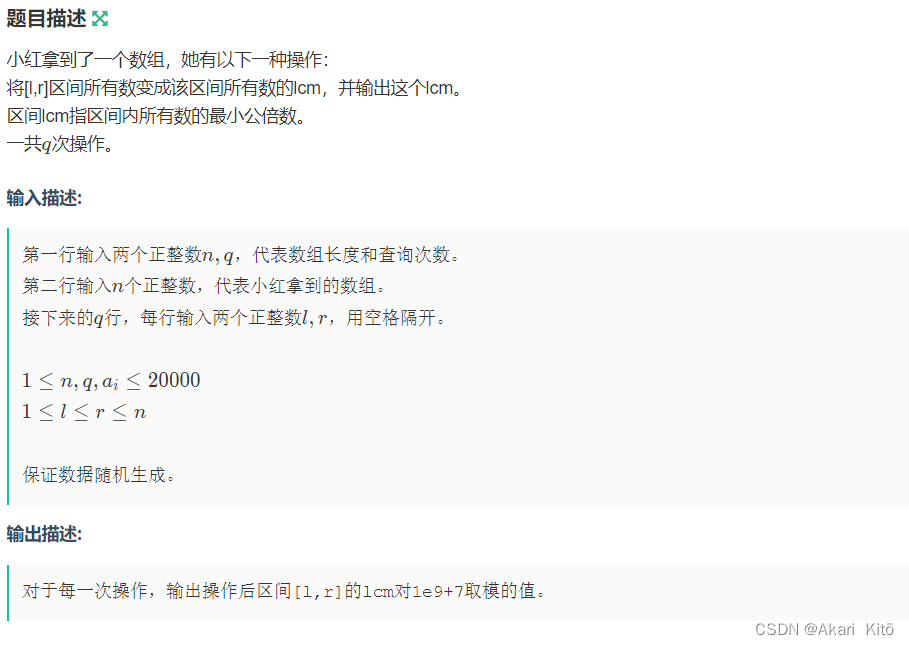
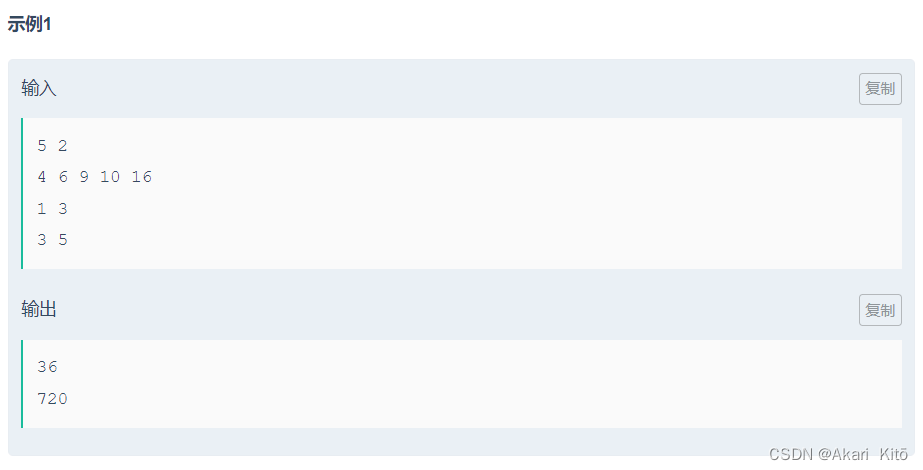
分析：
看题目特征，首先，题目数据随机生成，其次，存在区间推平操作，故可以考虑珂朵莉树。
另外，需要注意 $lcm(a,b)\%mod\ne lcm(a\%mod,b)$。故直接维护区间lcm是行不通的，由此我们质因数分解，维护每个质因数在区间内最多出现多少次方。20000以内的质数个数不是很多，不到2300个，再考虑的推平操作，考虑使用珂朵莉树。（线段树的话，由于要开4倍的空间，所以还是有点卡的）
AC代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll
typedef vector<int> vv;
#define itt set<node>::iterator
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

const int maxn = 20005;
const ll mod = 1e9 + 7;
int n, q, l, r, num;
ll ar[maxn];
struct node
{
    int l, r;
    vv vt;
    bool operator < (const node &b) const
    {
        return l < b.l;
    }
};
set<node> tree;
bool prime[maxn];
int Prime[maxn];
int pid[maxn];

void make_prime()
{
    memset(prime, true, sizeof(prime));
    memset(pid, -1, sizeof(pid));
    prime[0] = prime[1] = false;
    for(int i = 2; i <= maxn; i++)
    {
        if(prime[i])
        {
            Prime[num]=i;
            pid[i] = num++;
        }
        for(int j=0; j < num && i * Prime[j] < maxn; j++)
        {
            prime[i * Prime[j]] = false;
            if(!(i % Prime[j]))
                break;
        }
    }
}

ll pow_mod(ll a, ll n)
{
    ll ans = 1;
    a %= mod;
    while(n)
    {
        if(n & 1) ans = (ans * a) % mod;
        a = (a * a) % mod;
        n >>= 1;
    }
    return ans;
}

itt split(int pos)
{
    itt it = tree.lower_bound({pos, 0, {}});
    if(it != tree.end() && it -> l == pos) return it;

    --it;
    int l = it -> l;
    int r = it -> r;
    vector<int> v = it -> vt;
    tree.erase(it);
    tree.insert({l, pos - 1, v});
    return tree.insert({pos, r, v}).first;
}

void solve(int l, int r)
{
    itt itr = split(r + 1);
    itt itl = split(l);
//    cout << itl -> l << ' ' << itl -> r << '\n';
//    cout << itr -> l << ' ' << itr -> r << '\n';

    vector<int> vt(2300, 0);
    for(itt it = itl; it != itr; ++it)
    {
        //cout << it -> l << ' ' << it -> t << '\n';
        for(int i = 0; i < 2300; ++i)
        {
            vt[i] = max(vt[i], it->vt[i]);
            //cout << vt[i] <<
        }
    }

    ll ans = 1;
    for(int i = 0; i < 2300; ++i)
    {
        //cout << i << ' ' << vt[i] << ' ';
        ans = (ans * pow_mod(Prime[i], vt[i])) % mod;
        //cout << ans << '\n';
    }
    cout << ans << '\n';
    tree.erase(itl, itr);
    tree.insert(node{l, r, vt});
}

void print()
{
    for(itt it = tree.begin(); it != tree.end(); ++it)
    {
        cout << it -> l << ' ' << it -> r << '\n';
    }
}

signed main()
{
    io;
    make_prime();
//    for(int i = 0; i <= 100; ++i)
//    {
//        cout << i << ' ' << prime[i] << ' ' << Prime[i] << ' ' << pid[i] << '\n';
//    }

    cin >> n >> q;
    vector<int> vt(2300, 0);
    int cnt = 0;

    for(int i = 1; i <= n; ++i)
    {
        cin >> ar[i];
        vt.clear();
        vt = vector<int>(2300, 0);
        for(int j = 2; j * j <= ar[i]; ++j)
        {
            cnt = 0;
            while(ar[i] % j == 0)
            {
                ++cnt;
                ar[i] /= j;
            }
            if(pid[j] == -1) continue;
            vt[pid[j]] += cnt;
        }
        if(ar[i] > 1) ++vt[pid[ar[i]]];
        tree.insert(node{i, i, vt});
    }

    while(q--)
    {
        cin >> l >> r;
        solve(l, r);
        //print();
    }
    return 0;
}

三.区间操作

1.2022 ACM 湖北省赛 L (线段树)

题意：
输入长度为n的数组，q次询问，n个数字每个数字有两个权值，权值ar[i] (1 <= ar[i] <= 10^8),s[i](s[i]=0/1)。询问分为一下四种。
1 x : 将s[x]变成0，保证原来的 s[x] = 1
2 x : 将s[x]变成1，保证原来的 s[x] = 0
3 L R x : 给区间 [l,r] 中所有的s[i]=1的ar[i]都加上一个数
4 L R ： 输出区间 [l,r] 中的 ar[i] 的和
分析：
维护$\sum ar[i]$和$\sum s[i]$即可，由于是区间修改，所以还需要懒标记。
AC代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

const int maxn = 1e5 + 5;
int n, m;
int ar[maxn];
bool s[maxn];
struct node
{
    int l, r;
    int lazy_sum;
    int cnt, sum;

    int mid()
    {
        return (l + r) >> 1;
    }

    void print()
    {
        cout << l << ' ' << r << ' ' << lazy_sum << ' ' << cnt << ' ' << sum << '\n';
    }
} tree[maxn<<2];
int op, l, r, x;

void pushup(int p)
{
    tree[p].sum = tree[p<<1].sum + tree[p<<1|1].sum;
    tree[p].cnt = tree[p<<1].cnt + tree[p<<1|1].cnt;
}

void pushdown(int p)
{
    tree[p<<1].sum += tree[p<<1].cnt * tree[p].lazy_sum;
    tree[p<<1].lazy_sum += tree[p].lazy_sum;
    tree[p<<1|1].sum += tree[p<<1|1].cnt * tree[p].lazy_sum;
    tree[p<<1|1].lazy_sum += tree[p].lazy_sum;
    tree[p].lazy_sum = 0;
}

void build(int p, int l, int r)
{
    tree[p].l = l;
    tree[p].r = r;
    tree[p].lazy_sum = 0;

    if(l == r)
    {
        tree[p].sum = ar[l];
        tree[p].cnt = s[l];
        return ;
    }

    int mid = (l + r) >> 1;
    build(p<<1, l, mid);
    build(p<<1|1, mid + 1, r);
    pushup(p);
}

void updata1(int p, int pos)
{
    if(tree[p].l == tree[p].r)
    {
        tree[p].cnt ^= 1;
        return ;
    }

    if(tree[p].lazy_sum) pushdown(p);
    int mid = (tree[p].l + tree[p].r) >> 1;
    if(pos <= mid) updata1(p<<1, pos);
    else updata1(p<<1|1, pos);
    pushup(p);
}

void updata2(int p, int l, int r, int x)
{
    if(l <= tree[p].l && tree[p].r <= r)
    {
        tree[p].sum += tree[p].cnt * x;
        tree[p].lazy_sum += x;
        return ;
    }

    if(tree[p].lazy_sum) pushdown(p);
    int mid = (tree[p].l + tree[p].r) >> 1;
    if(l <= mid) updata2(p<<1, l, r, x);
    if(r > mid) updata2(p<<1|1, l, r, x);
    pushup(p);
}

ll query(int p, int l, int r)
{
    if(l <= tree[p].l && tree[p].r <= r) return tree[p].sum;

    if(tree[p].lazy_sum) pushdown(p);
    int mid = (tree[p].l + tree[p].r) >> 1;
    ll res = 0;
    if(l <= mid) res = query(p<<1, l, r);
    if(r > mid) res += query(p<<1|1, l, r);

    return res;
}

signed main()
{
    io;
    cin >> n >> m;
    for(int i = 1; i <= n; ++i) cin >> ar[i];
    for(int i = 1; i <= n; ++i) cin >> s[i];

    build(1, 1, n);

//    for(int i = 1; i <= 3 * n; ++i)
//    {
//        cout << i << ' ';
//        tree[i].print();
//    }

    while(m--)
    {
        cin >> op;
        if(op == 1 || op == 2)
        {
            cin >> x;
            updata1(1, x);
//            for(int i = 1; i <= 7; ++i)
//            {
//                cout << i << ' ';
//                tree[i].print();
//            }
        }
        else if(op == 3)
        {
            cin >> l >> r >> x;
            updata2(1, l, r, x);
//            for(int i = 1; i <= 7; ++i)
//            {
//                cout << i << ' ';
//                tree[i].print();
//            }
        }
        else
        {
            cin >> l >> r;
            cout << query(1, l, r) << '\n';
//            for(int i = 1; i <= 7; ++i)
//            {
//                cout << i << ' ';
//                tree[i].print();
//            }
        }
    }

    return 0;
}

2.2022牛客寒假算法基础集训营4 B-进制 (线段树)

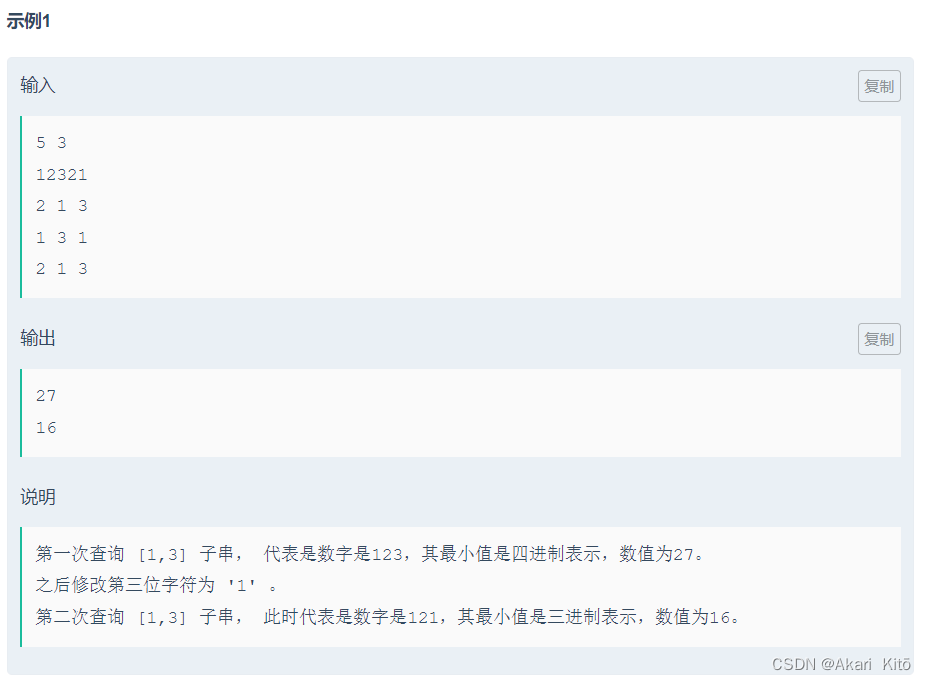
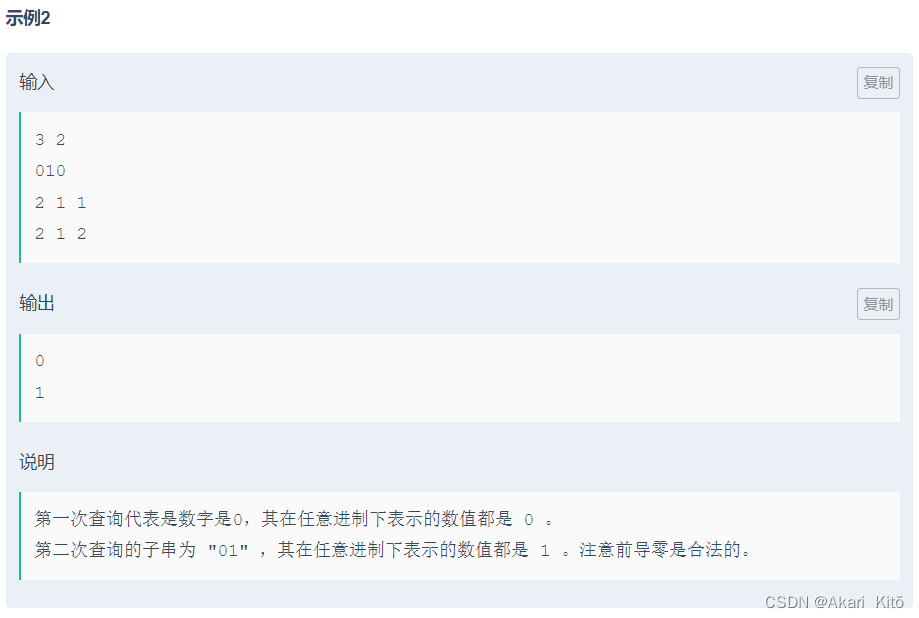
分析：
维护区间最大值，和作为i进制数的大小即可维护。
AC代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define endl '\n'

const int maxn = 1e5 + 5;
const ll mod = 1e9 + 7;
const ll inf = 0x3f3f3f3f;
struct node
{
    int l, r, mx;
    int ar[12];

    int mid()
    {
        return (l + r) >> 1;
    }

    void print()
    {
        cout << l << ' ' << r << ' ' << mx << '\n';
        for(int i = 1; i <= 10; ++i) cout << ar[i] << ' ';
        cout << '\n';
    }
}tree[maxn<<2];
int n, q, op, x, y;
string s;
node ans;

ll pow_mod(ll a, ll n)
{
    ll ans = 1;
    a %= mod;
    while(n)
    {
        if(n & 1) ans = (ans * a) % mod;
        a = (a * a) % mod;
        n >>= 1;
    }
    return ans;
}

void pushup(node &p, node &le, node &ri)
{
    p.mx = max(le.mx, ri.mx);
    p.l = le.l;
    p.r = ri.r;
    for(int i = 1; i <= 10; ++i)
    {
        if(i <= p.mx) p.ar[i] = inf;
        else p.ar[i] = ((le.ar[i] * pow_mod(i, ri.r - ri.l + 1)) % mod + ri.ar[i]) % mod;
    }
}

void pushup(int p)
{
    pushup(tree[p], tree[p<<1], tree[p<<1|1]);
}

void build(int p, int l, int r)
{
    tree[p].l = l;
    tree[p].r = r;

    if(l == r)
    {
        tree[p].mx = s[l] - '0';
        for(int i = 1; i <= 10; ++i)
        {
            if(i <= tree[p].mx) tree[p].ar[i] = inf;
            else tree[p].ar[i] = tree[p].mx;
        }
        return ;
    }

    int mid = (l + r) >> 1;
    build(p<<1, l, mid);
    build(p<<1|1, mid + 1, r);
    pushup(p);
}

void updata(int p, int x, int y)
{
    if(tree[p].l == tree[p].r)
    {
        tree[p].mx = y;
        for(int i = 1; i <= 10; ++i)
        {
            if(i <= tree[p].mx) tree[p].ar[i] = inf;
            else tree[p].ar[i] = tree[p].mx;
        }
        return ;
    }

    int mid = tree[p].mid();
    if(x <= mid) updata(p<<1, x, y);
    else updata(p<<1|1, x, y);
    pushup(p);
}

node query(int p, int l, int r)
{
    if(l <= tree[p].l && tree[p].r <= r) return tree[p];

    int mid = tree[p].mid();
    if(mid >= r) return query(p<<1, l, r);
    else if(mid < l) return query(p<<1|1, l, r);
    else
    {
        node res;
        node le = query(p<<1, l, r);
        node ri = query(p<<1|1, l, r);
        pushup(res, le, ri);
        return res;
    }
}

signed main()
{
    io;

    cin >> n >> q;
    cin >> s;
    s = " " + s;

    build(1, 1, n);

//    for(int i = 1; i <= 9; ++i)
//    {
//        cout << i << ' ';
//        tree[i].print();
//    }

    while(q--)
    {
        cin >> op >> x >> y;
        if(op == 1) updata(1, x, y);
        else
        {
            ans = query(1, x, y);
            cout << ans.ar[ans.mx + 1] << '\n';
        }
    }

    return 0;
}

3.Codeforces Round #254 (Div. 1) C. DZY Loves Colors (线段树)

分析：
维护区间权值和，区间的颜色，如果区间内颜色统一则区间修改，使用lazy标记，不统一则暴力单点修改。
AC代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
#define int ll
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define endl '\n'
#define itt set<node>::iterator

const int maxn = 1e5 + 5;
const ll mod = 1e9 + 7;
const ll inf = 0x3f3f3f3f;
struct node
{
    int l, r;
    int color, sum, cnt;
    int lazy;
    bool flag;

    int mid()
    {
        return (l + r) >> 1;
    }

    void print()
    {
        cout << l << ' ' << r << ' ' << color << ' ' << flag << ' ' << sum << ' '<< cnt << ' ' << lazy << '\n';
    }
}tree[maxn<<2];
int n, m, op, l, r, x;

void pushup(int p)
{
    tree[p].sum = tree[p<<1].sum + tree[p<<1|1].sum;
    tree[p].flag = false;
    tree[p].color = 0;
    if(tree[p<<1].flag && tree[p<<1|1].flag && tree[p<<1].color == tree[p<<1|1].color)
    {
        tree[p].flag = true;
        tree[p].color = tree[p<<1].color;
    }
}

void pushdown(int p)
{
    tree[p<<1].sum += tree[p<<1].cnt * tree[p].lazy;
    tree[p<<1].lazy += tree[p].lazy;
    tree[p<<1].color = tree[p].color;
    tree[p<<1|1].sum += tree[p<<1|1].cnt * tree[p].lazy;
    tree[p<<1|1].lazy += tree[p].lazy;
    tree[p<<1|1].color = tree[p].color;
    tree[p].lazy = 0;
}

void build(int p, int l, int r)
{
    tree[p].l = l;
    tree[p].r = r;
    tree[p].cnt = r - l + 1;
    tree[p].lazy = 0;

    if(l == r)
    {
        tree[p].color = l;
        tree[p].flag = true;
        tree[p].sum = 0;
        return ;
    }

    int mid = tree[p].mid();
    build(p<<1, l, mid);
    build(p<<1|1, mid + 1, r);
    pushup(p);
}

void updata(int p, int l, int r, int x)
{
    if (tree[p].l > r || tree[p].r < l) return;
    if(l <= tree[p].l && tree[p].r <= r && tree[p].flag)
    {
        tree[p].sum += tree[p].cnt * abs(tree[p].color - x);
        tree[p].lazy += abs(tree[p].color - x);
        tree[p].color = x;
        return ;
    }

    if(tree[p].lazy) pushdown(p);
    updata(p<<1, l, r, x);
    updata(p<<1|1, l, r, x);
    pushup(p);
}

ll query(int p, int l, int r)
{
    if(tree[p].l > r || tree[p].r < l) return 0;
    if(l <= tree[p].l && tree[p].r <= r) return tree[p].sum;

    if(tree[p].lazy) pushdown(p);
    return query(p<<1, l, r) + query(p<<1|1, l, r);
}

signed main()
{
    io;

    cin >> n >> m;

    build(1, 1, n);

    while(m--)
    {
        cin >> op;
        if(op == 1)
        {
            cin >> l >> r >> x;
            updata(1, l, r, x);
        }
        else
        {
            cin >> l >> r;
            cout << query(1, l, r) << '\n';
        }
    }

    return 0;
}