图文并茂 —— 插入排序,希尔排序

每博一文案
杨绛先生曾说:世态人情,可做书读,可当细看。行走在人生的旅途中,
遇见的人数不胜数,结识的朋友也越来越多,走过半身,尝遍人情冷暖,
后领悟到一句话的真谛。水不适,不知深浅,人不交,不知好坏。
世界上最不可估量的就是复杂善变的人心。
很多时候,我们之所以感到痛苦和心累,是因为期望和想要的太多,
得到的太少,不愿放弃的太多,开花结果的的太少,期望太多就会变成执念,
执念太深,所以才有遗憾。
文章目录
一. 插入排序
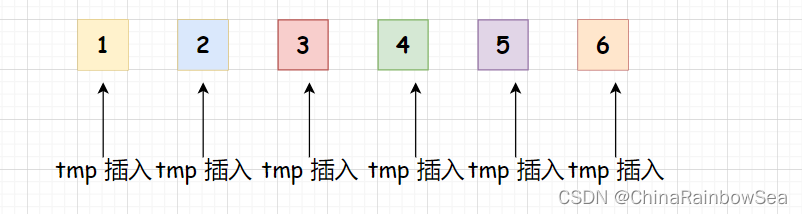
插入排序 是一种简单的插入排序法,其基本的思想是:把待排序的记录按其数值的大小逐个 插入到一个已经排序好的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。。说白一点就是把数据插入到对应有序的位置处:就像我们打扑克牌的时候,我们每摸一张牌都会,将其插入到对应有序的位置上,如从小到大,把数值大的牌放到右边,小的放到左边,方便查看使用,提高出牌的速度。



插入排序具体步骤
这里以升序为例
步骤
默认数组的下标位置 0 是为有序的,排序后面的数值就可以了,通过排序后面的数值的时候,会更新到 数组下标为 0 的数值排序到
把插入的数据向前作比较判断,通过比较判断,进行数值上的移动调换位置,
在升序这里,如果插入的数值小于在该数值下标前面的位置,其前面的数值后移动,如果插入的数值大于其前面的数值,则停止移动,将该数值插入到小于该数值的下标的后面。
注意移动过程中,防止数组的越界情况
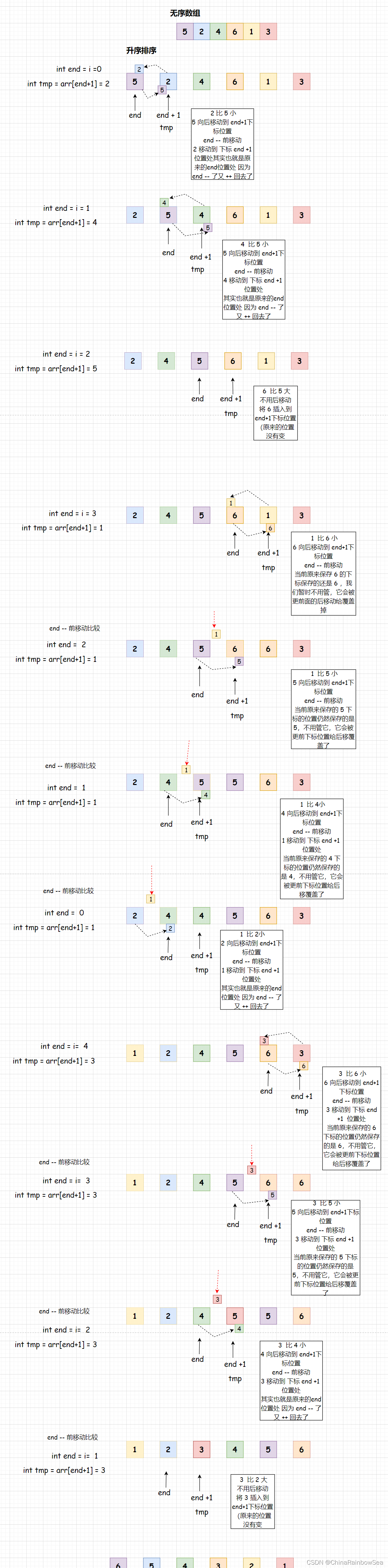
下面是一个简单的 插入排序的动图:大家可以多观察其中的移动方式

插入排序代码实现思路
- 明确我们排序的对象是一个无序的数组,默认数组的第一个数值是有序的(因为后面插入排序的数值会把该位置的数值也比较的,从而实现了 第一个数值也是排序到了,而且如果从数组下标为 0 ,开始作为插入排序的对象的话,自己跟自己比较排序一下,没有意义,还浪费了一次插入的性能),我们对数组中的第二个数值(后一个下标的数值)进行插入判断排序。说白了默认数组下标为0 的数值是有序的排序好了,就是从数组下标为 1 的位置的数值开始往后数组中取数值作为插入排序的对象 ,直到,取到把数组中最后一个数据给插入排序完。
- 取出数组中插入排序的数值(就是数组下标为 0 的后一个下标),保存到一个变量中,防止其被后面的移动,给覆盖了。
- 对插入排序的数值进行,从上面的动图演示:就可以看出下标是向前走的,比较数值判断,因为无论是升序还是降序,其数值都是把 越小的数值(升序)或越大的数值(降序) 往数组下标前的位置送的。
- 这里是以升序为例的,当插入排序(tmp)的对象数值,小于( < ) 其下标(end)前面的数值的时候,前面的数值后移动覆盖掉原来(arr[end+1] = arr[end] ) 插入排序的位置的数值,然后下标前移 (end–),继续重复这样的操作,直到数组下标到 0 或者是前面的下标位置的数值 < 插入排序的数值的时候,将该插入排序的数值插入到该下标的后面一位的地方处(arr[end+1] = tmp)。重复以上操作,直到数组中的全部数值都插入排序完。
- 后该数组就是有序的了
具体的代码实现如下:
// 插入排序,升序
void InsertSortAsc(int* arr, int n)
{
// 注意 1. i < n -1
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = arr[end + 1]; // 保存一个下标的数值,防止移动被覆盖
while (end >= 0) // 防止移动越界
{
if (tmp < arr[end]) // tmp < 数组该下标的位置,当前下标的数值,后移动,覆盖
{
arr[end + 1] = arr[end]; // 后移动,覆盖
end--; // 向前继续判断,移动
}
else // 当 tmp >= 其前面下标对应的数值的时候,跳出循环,插入到该下标的后面
{
break;
}
}
// 这里升序,当 tmp 为最小时,会前移动到 下标为 -1 ,
// end-- 的位置,跳出循环,将数值tmp 插入到 -1 下标的后面,
// 即 end(-1) +1 = 0 , 就是数组最开头位置
arr[end + 1] = tmp; // 插入数值 tmp ,到该 <= 数值的后面一个位置 end+1
}
}
运行结果
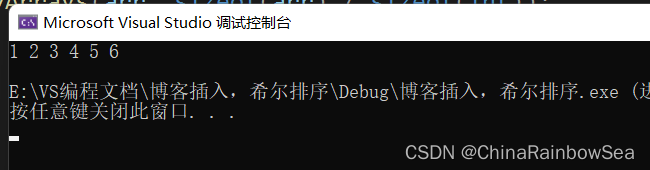
其插入排序代码刨析
如下图:运行上的解析
注意我们的 i = end < n-1 只能访问到数组的倒数第二个位置的数值,因为我们的 end+1 每次取的都是在其 i=end 下标后面的==+1== 的位置的数值,所以当 i=end 在数组倒数第二个位置处时,已经有 end+1 访问到数组最后一个数值了。而如果 i = end < n ,那么end +1 就会访问到数组越界了。
还有一点 while( end >= 0) 的循环条件,防止 end– 过头越界了,数组的下标是从 0 开始的,当在数值判断上 升序 ,tmp 插入对象 小于 其前下标的数值时,前面大的数值后移动覆盖,并且 end– ,继续向前比较判断,当 tmp 大于 或等于 其前面下标的数值,跳出循环,进行插入数值操作:把 tmp 的数值插入到 大于或等于 其数值的下标的后一个下标处 end +1 ; 重复上述操作,直到数组中的所有数值都遍历判断过,则数组就是有序的了。
插入排序的,降序排序
就是简单的把 if (tmp > arr[end]) ,就是让更大的数值放到数组的最开头
具体降序代码实现
// 插入排序的,降序
void InsertSortDesc(int* arr, int n)
{
// i < n-1 防止 end +1 越界访问
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = arr[end + 1]; // 后一个下标,为插入对象,保存起来,防止移动覆盖了
while (end >= 0) // 防止 end -- 数组越界访问了
{
if (tmp > arr[end]) // 降序,tmp 大 ,前移动
{
arr[end + 1] = arr[end]; // 小的,后移动
end--; // 前移动,继续比较判断
}
else // tmp 小于或等于 前面下标的数值,跳出循环,插入操作
{
break;
}
}
arr[end + 1] = tmp; // 将数值插入到后面的 tmp <|= 的下标后面+1 的位置处
}
}
运行结果
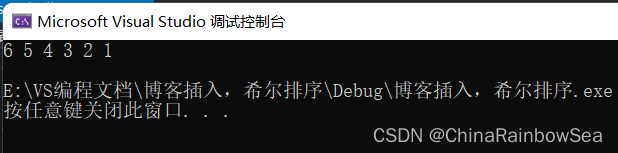
插入排序的特点
- 元素集合越接近有序,直接插入排序算法的时间效率越高,因为越有序,其移动的数值就越少,效率就越高,后面的希尔排序 就是基于这种方式的优化
- 时间复杂度: O(N^2),注意是以最坏的情况下,这里以升序为例,最坏的情况是:逆序 的时候:需要移动的是将复杂度为 O(n(n -1))
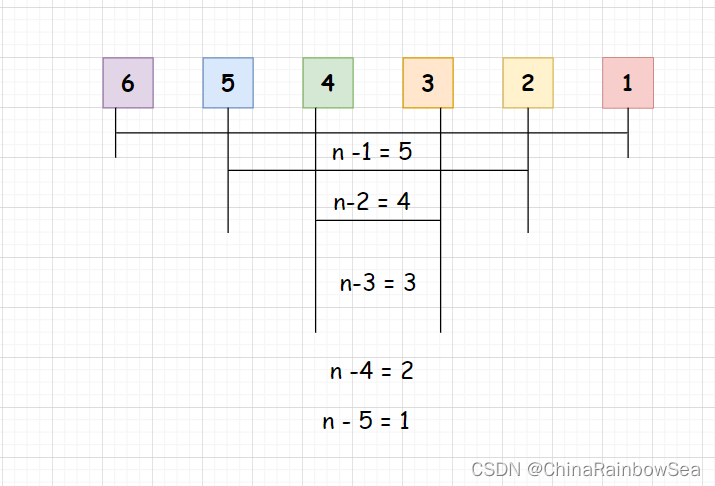
最好的情况是在,升序的情况下的 顺序 ,所需移动的时间复杂度为: O(n),因为本身就是顺序升序的所以,只要不会进入第二层的循环,直接插入操作就可以了。
- 稳定性: 稳定
二. 希尔排序
希尔排序 : 是D.L.Shell 于 1959年提出来的一种排序算法,在这之前排序算法的时间复杂度都是O(n^2), 希尔排序算法是突破这个时间复杂度的第一批算法之一。希尔排序算法的发明,使得我们终于突破了,慢速排序的时代(超越了时间复杂度O(n^2)) ,之后,相应的更为高效的排序算法也就相继出现了。
2.1 希尔排序算法概念
从上面的直接插入排序中,我们可以看到,它的效率在某些时候是很高的,比如:我们的数组本身就是基本有序的,我们只需要少量的插入操作,就可以完成整个记录集的排序工作,此时直接插入很高效。还有就是数组数量比较少的时候,直接插入的优势也比较明显。可问题在于,两个条件本身就过于苛刻,现实中记录少或者本身有序就属于特殊情况。
不过别急,有条件当然很好,条件不存在,我们就创造条件也是可以去做的。于是,科学家希尔研究出了一种排序方法,对直接插入排序改进可以提高效率。
如何让待排序的记录个数较少呢? ,很容易想到的就是将原本有大量记录数的记录进行分组,分割成若干个序列,此时每个子序列待排序的记录个数就比较少了,然后在这些子序列内分别进行了直接插入排序,当整个序列都基本有序时,注意:只是基本有序时,再对全体记录进行一个直接插入排序后,该记录的数据就是有序的了。
基本有序 : 升序 中指的是: 数值小的放到数组的前面,数值大的放到数组的后面,不大不小的放到数组的中间。降序 数值大的放到数组的前面,数值小的放到数组的后面,不大不小的放到数组的中间。
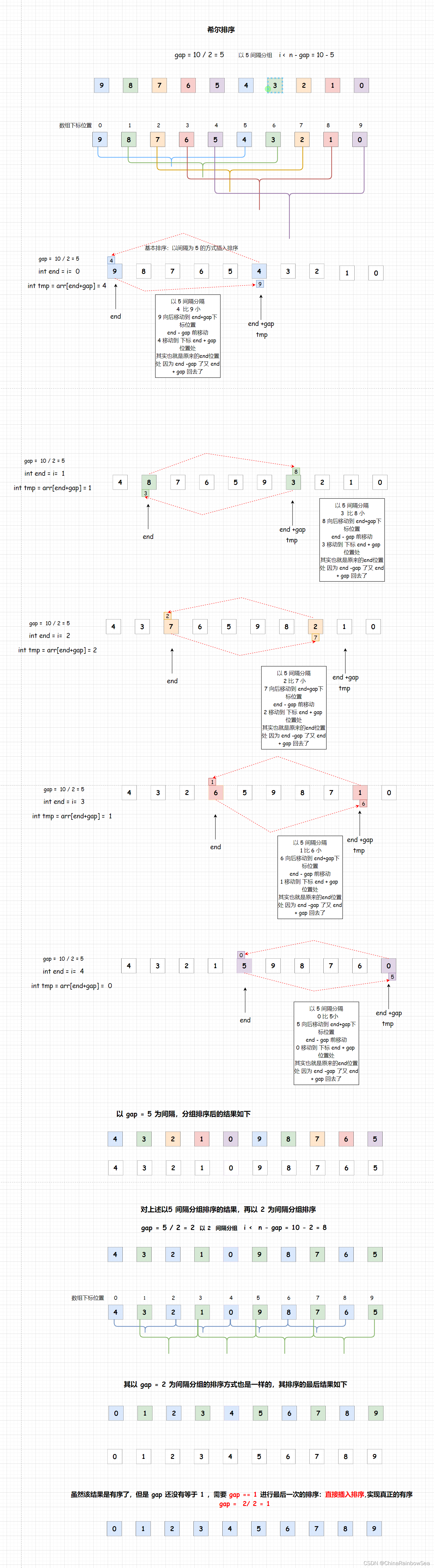
希尔排序法 又称为时缩小增量法。希尔排序法的基本思想是: 先选定一个整数,把待排序文件中所有 记录分成个组,所有距离为 gap 的记录分在同一组内,并对每一组内的记录进行排序(排序的方法和插入排序的方法是一样的,不过是下标之间的分组间隔不同了,而已),然后,取,重复上述分组和排序的工作。当到达了 gap =1 的时候,就是插入排序,所有的记录都排序好了。
如下动图演示

注意对于 gap 的选取要根据 数组的大小变化,而不是固定的的方式,并且 gap 的最后一次排序 一定要为 1 ,进行直接的插入排序。
希尔排序的步骤
- 进行基本排序 ,以不同的 gap 间隔分组排序(排序方式和插入排序是一样的),
- 最后一次 ,gap == 1,进行直接插入排序,让数组完整的有序
希尔排序,升序:具体代码实现如下:
// 希尔排序,升序
/* 1.基本排序
* 2.gap == 1,进行直接插入排序
*/
void ShellSortAsc(int* arr, int n)
{
int gap = n; // 分组间隔
while (gap > 1) // gap > 1 防止进行过多的不必要的,分组,如 gap = 0 时,1 中已经在内中排序过了
{
gap = gap / 2;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = arr[end + gap]; // 保留以 gap 间隔分组的 下一个下标位置的数值,防止移动被覆盖
while (end >= 0) // 防止数组越界访问
{
if (tmp < arr[end]) // 升序,tmp < 其以 gap 间隔分组的前一个下标位置的数值,
{ // tmp 前走继续判断,gap大于的后移动
arr[end + gap] = arr[end]; // 注意后移的下一个下标位置是以 gap 间隔的位置
end = end - gap; // 前移动,继续比较判断
}
else // 当tmp >= 其以 gap 间隔分组的前一个下标位置的数值,跳出循环,
{ // 进行插入操作
break;
}
}
arr[end + gap] = tmp; // 注意是以gap 为间隔分组的,所以下一个下标的位置是 + gap的,不是+1
}
}
}
希尔排序代码解剖
在该代码中我们有几个注意的点:
- while (gap > 1),防止 gap = 0 ,导致 gap /2 = 0/2 = 0 ,没有意义的间隔分组,什么以 0 间隔分组的吗 ? ? ?
- for (int i = 0; i < n - gap; i++) 中的 i < n -gap,防止数组中的进行过度不必要的分组,只需要取数组其中的 n -gap 个数值,就可以把数组中的全部数值都遍历排序到的。
- while (end >= 0), 防止数组越界访问,报错,因为 后面的循环条件的更新是 end = end - gap ,注意这里 的数值间隔排序是 以 gap 为间隔的,所以 数组之间的下一个下标位置是 end + gap,以及向前判断的,下标的移动 end = end - gap ,遍历数组 n < gap 个对象数值
观察 gap 的变化对数值中的排序的影响
- gap 越大,大的数值就越快排到后面,小的数就越快排到前面
- gap 越大 ,基本排序完后,其结果就越不接近有序
- gap 越小,就越接近有序,甚至是有序
- 当gap == 1, 的时候,就是直接插入排序,变成了有序了。
注意: gap 不能固定,要与数组的长度变化,因为如果你的数组为 10000 时,你还 gap = 3 的间隔排序的话,那就跟没有作 基本排序的插入排序没有太大区别了,因为gap 由大到小变化的排序,一步一步的 gap 的间隔排序,都在为后面的 gap 变小的排序中,减少移动的数据量,效率就越快,如果一开始就那么小的话,根本就没有为移动的数据量减少多少。并且 最后一次 gap 一定要为 1进行直接的插入排序,才能保证排序是有序的 , gap 有两种表示:
- gap = n / 2 , 这样 gap > 1, 无论 gap 变化为多少,最后都可以变成 1,如: 3 /2 = 1
- gap = n /3 +1 ,同样无论 gap 变化为 多少,最后都可以便变成 1,如:2 / 3 = 0 + 1 = 1
希尔排序,降序
与 插入排序一样只要将 if (tmp < arr[end]) 改为 if (tmp > arr[end]) 即可,把大的数值往数组的前面移动,小的数值往数组的后面移动
// 希尔排序,降序
void ShellSortDesc(int* arr, int n)
{
int gap = n; // gap 的设定
while (gap > 1) // gap 不为 0 ,防止 gap = 0 无用的间隔分组排序
{
gap = gap / 2;
for (int i = 0; i < n - gap; i++) // n - gap 足够遍历全部数组的数值了,过多了没有必要
{
int end = i;
int tmp = arr[end + gap]; // 下一个下标位置是以 gap 为间隔的
while (end >= 0)
{
if (tmp > arr[end]) // tmp 大于 前面下标的位置,前面的下标数值后移,以 gap 为间隔
{
arr[end - gap] = arr[end]; // 前面小的数值,后移
end = end - gap; // 下标移动,继续比较判断
}
else // 前面下标的数值 >= tmp ,跳出循环,tmp 插入到后面的下标位置处
{
break;
}
}
// 跳出循环
arr[end + gap] = tmp; // tmp 插入到该下标的后面,以gap 为间隔
}
}
}

2.2 希尔排序的特点
- 时间复杂度为 :最坏的情况下,gap = n / 2 为 O(N*log2^N),gap = n /3 +1 为O(N* long3^N)
- 稳定性:不稳定
2.3 希尔排序与 插入排序的 共同点
从上面的 希尔排序 与 插入排序 中的对比上我们可以发现到,希尔排序 其实就是插入排序 在有序的条件下排序效率高,上的条件的创建,希尔排序通过基本排序(gap 间隔分组)对数组中的数据进行预排序,每一次的预排序,都使数组中的数据更加有序,大大减少了最后一次,gap = 1的插入排序中移动的数据量,大大提高了,排序效率
三. 希尔排序, 插入排序的实际性能测试
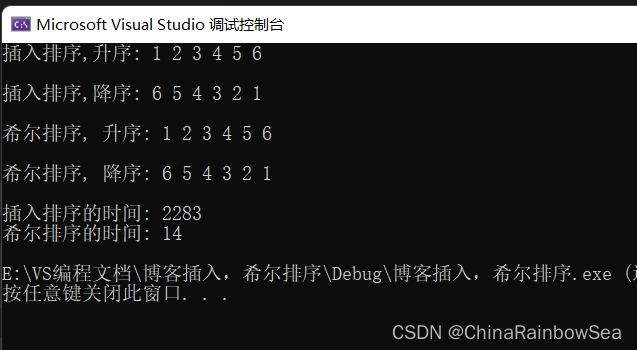
下面我们创建一个 10 万的数组,并通过随机值为数组赋值,在通过计算 运行排序完排序之后的时间点 -(减去) 运行排序之前的时间点,得到运行完排序后的之间:具体代码实现如下
// 排序的性能测试
void TestOP()
{
srand(time(0)); // 时间种子
const int N = 100000; // 定义常量 10W 个空间的数组
int* arr1 = (int*)malloc(sizeof(int) * N); // 动态堆区内存开辟空间
int* arr2 = (int*)malloc(sizeof(int) * N);
// 判断堆区开辟的空间是否成功
if (NULL == arr1 || NULL == arr2)
{
perror("malloc error"); // 提示报错
exit(-1); // 非正常退出程序
}
for (int i = 0; i < N; i++)
{
arr1[i] = rand(); // 产生随机值
arr2[i] = arr1[i]; // 让数组中的数值一样,控制变量,排序
}
int befin1 = clock(); // 保存, 插入排序前的时间点
InsertSortAsc(arr1, N); // 插入排序,升序
int end1 = clock(); // 保存, 插入排序完的时间点
int befin2 = clock(); // 保存, 希尔排序前的时间点
ShellSortAsc(arr2, N); // 希尔排序, 升序
int end2 = clock(); // 保存, 希尔排序完的时间点
/* 排序的所需时间 = 排序完的时间 end - befin 排序前的时间
*/
printf("插入排序的时间: %d\n", end1 - befin1);
printf("希尔排序的时间: %d\n", end2 - befin2);
// 释放堆区上开辟的空间,并手动置为 NULL
free(arr1);
arr1 = NULL;
free(arr2);
arr2 = NULL;
}

从运行结果上看,可以明显看出 希尔排序的速度是 插入排序的 100 倍,随着排序的数据量的增加,其倍速越大。
四. 完整代码实现
有关于该排序中的完整代码如下: 大家可以将代码直接复制到 VS 2019 中可以直接运行测试
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
// 打印数组
void playArrays(int* arr, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
// 插入排序,升序
void InsertSortAsc(int* arr, int n)
{
// 注意 1. i < n -1
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = arr[end + 1]; // 保存一个下标的数值,防止移动被覆盖
while (end >= 0) // 防止移动越界
{
if (tmp < arr[end]) // tmp < 数组该下标的位置,当前下标的数值,后移动,覆盖
{
arr[end + 1] = arr[end]; // 后移动,覆盖
end--; // 向前继续判断,移动
}
else // 当 tmp >= 其前面下标对应的数值的时候,跳出循环,插入到该下标的后面
{
break;
}
}
// 这里升序,当 tmp 为最小时,会前移动到 下标为 -1 ,
// end-- 的位置,跳出循环,将数值tmp 插入到 -1 下标的后面,
// 即 end(-1) +1 = 0 , 就是数组最开头位置
arr[end + 1] = tmp; // 插入数值 tmp ,到该 <= 数值的后面一个位置 end+1
}
}
// 插入排序的,降序
void InsertSortDesc(int* arr, int n)
{
// i < n-1 防止 end +1 越界访问
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = arr[end + 1]; // 后一个下标,为插入对象,保存起来,防止移动覆盖了
while (end >= 0) // 防止 end -- 数组越界访问了
{
if (tmp > arr[end]) // 降序,tmp 大 ,前移动
{
arr[end + 1] = arr[end]; // 小的,后移动
end--; // 前移动,继续比较判断
}
else // tmp 小于或等于 前面下标的数值,跳出循环,插入操作
{
break;
}
}
arr[end + 1] = tmp; // 将数值插入到后面的 tmp <|= 的下标后面+1 的位置处
}
}
// 希尔排序,升序
/* 1.基本排序
* 2.gap == 1,进行直接插入排序
*/
void ShellSortAsc(int* arr, int n)
{
int gap = n; // 分组间隔
while (gap > 1) // gap > 1 防止进行过多的不必要的,分组,如 gap = 0 时,1 中已经在内中排序过了
{
gap = gap / 2;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = arr[end + gap]; // 保留以 gap 间隔分组的 下一个下标位置的数值,防止移动被覆盖
while (end >= 0) // 防止数组越界访问
{
if (tmp < arr[end]) // 升序,tmp < 其以 gap 间隔分组的前一个下标位置的数值,
{ // tmp 前走继续判断,gap大于的后移动
arr[end + gap] = arr[end]; // 注意后移的下一个下标位置是以 gap 间隔的位置
end = end - gap; // 前移动,继续比较判断
}
else // 当tmp >= 其以 gap 间隔分组的前一个下标位置的数值,跳出循环,
{ // 进行插入操作
break;
}
}
arr[end + gap] = tmp; // 注意是以gap 为间隔分组的,所以下一个下标的位置是 + gap的,不是+1
}
}
}
// 希尔排序,降序
void ShellSortDesc(int* arr, int n)
{
int gap = n; // gap 的设定
while (gap > 1) // gap 不为 0 ,防止 gap = 0 无用的间隔分组排序
{
gap = gap / 2;
for (int i = 0; i < n - gap; i++) // n - gap 足够遍历全部数组的数值了,过多了没有必要
{
int end = i;
int tmp = arr[end + gap]; // 下一个下标位置是以 gap 为间隔的
while (end >= 0)
{
if (tmp > arr[end]) // tmp 大于 前面下标的位置,前面的下标数值后移,以 gap 为间隔
{
arr[end + gap] = arr[end]; // 前面小的数值,后移
end = end - gap; // 下标移动,继续比较判断
}
else // 前面下标的数值 >= tmp ,跳出循环,tmp 插入到后面的下标位置处
{
break;
}
}
// 跳出循环
arr[end + gap] = tmp; // tmp 插入到该下标的后面,以gap 为间隔
}
}
}
// 排序的性能测试
void TestOP()
{
srand(time(0)); // 时间种子
const int N = 100000; // 定义常量 10W 个空间的数组
int* arr1 = (int*)malloc(sizeof(int) * N); // 动态堆区内存开辟空间
int* arr2 = (int*)malloc(sizeof(int) * N);
// 判断堆区开辟的空间是否成功
if (NULL == arr1 || NULL == arr2)
{
perror("malloc error"); // 提示报错
exit(-1); // 非正常退出程序
}
for (int i = 0; i < N; i++)
{
arr1[i] = rand(); // 产生随机值
arr2[i] = arr1[i]; // 让数组中的数值一样,控制变量,排序
}
int befin1 = clock(); // 保存, 插入排序前的时间点
InsertSortAsc(arr1, N); // 插入排序,升序
int end1 = clock(); // 保存, 插入排序完的时间点
int befin2 = clock(); // 保存, 希尔排序前的时间点
ShellSortAsc(arr2, N); // 希尔排序, 升序
int end2 = clock(); // 保存, 希尔排序完的时间点
/* 排序的所需时间 = 排序完的时间 end - befin 排序前的时间
*/
printf("插入排序的时间: %d\n", end1 - befin1);
printf("希尔排序的时间: %d\n", end2 - befin2);
// 释放堆区上开辟的空间,并手动置为 NULL
free(arr1);
arr1 = NULL;
free(arr2);
arr2 = NULL;
}
void test()
{
int arr[] = { 5,2,4,6,1,3 };
// 插入排序,升序
printf("插入排序,升序: ");
InsertSortAsc(arr, sizeof(arr) / sizeof(int));
/* sizeof(arr) 表示数组的总大小 单位字节
sizeof(int) 表示存放数组元素中的类型大小,单位字节
sizeof(arr)/sizeof(int) 表示计算数组的大小
*/
// 打印数组
playArrays(arr, sizeof(arr) / sizeof(int));
printf("\n");
// 插入排序,降序
printf("插入排序,降序: ");
InsertSortDesc(arr, sizeof(arr) / sizeof(int));
playArrays(arr, sizeof(arr) / sizeof(int));
printf("\n");
// 希尔排序,升序
printf("希尔排序, 升序: ");
ShellSortAsc(arr, sizeof(arr) / sizeof(int));
playArrays(arr, sizeof(arr) / sizeof(int));
printf("\n");
// 希尔排序,降序
printf("希尔排序, 降序: ");
ShellSortDesc(arr, sizeof(arr) / sizeof(int));
playArrays(arr, sizeof(arr) / sizeof(int));
printf("\n");
}
int main()
{
// 插入,希尔排序测试
test();
// 插入, 希尔排序性能测试
TestOP();
return 0;
}
最后;
限于自身水平,其中存在的错误,希望大家给予指教,韩信点兵——多多益善,谢谢大家,后会有期,江湖再见 !!!