通用算法与深度学习基础

发布于：2025-08-01 ⋅ 阅读:(15) ⋅ 点赞:(0)

秋招抱佛脚之作，由GPT提供内容大纲。

此博客每日更新，直至博主本人拿到满意的算法offer为止。

目录

1. 数学与概率统计

(1)线性代数：矩阵乘法、特征值/特征向量、SVD、PCA 原理★★★★★

(2)概率论：条件概率、贝叶斯公式、联合分布、期望/方差★★★★★

(3)最大似然估计与最大后验估计★★★★★

(4)信息论：熵、交叉熵、KL散度、互信息★★★★☆

(5)优化理论：梯度下降、牛顿法、动量法、Adam、学习率调度★★★★★

(6)凸优化与约束优化基础★★★☆☆

高数基础：偏导数链式法则、泰勒展开★★★☆☆

2. 机器学习基础

(1)经典算法：逻辑回归、SVM、KNN、朴素贝叶斯、决策树★★★★★

集成方法：Random Forest、GBDT、XGBoost、LightGBM★★★★★

模型评估：ROC/AUC、Precision-Recall、F1-score、混淆矩阵★★★★★

欠拟合与过拟合解决方案：正则化、数据增强、早停★★★★★

特征工程：标准化/归一化、特征交互、降维（PCA、t-SNE）★★★★☆

超参数搜索：网格搜索、随机搜索、Bayesian Optimization  ★★★★☆

3. 深度学习核心

神经网络基本结构：前向传播/反向传播★★★★★

CNN：卷积/池化、padding、stride、感受野★★★★★

RNN / LSTM / GRU：序列建模原理★★★★☆

Transformer 架构：多头注意力、位置编码、残差连接★★★★★

残差网络、DenseNet 与梯度流问题★★★★★

归一化技术：BN vs LN vs GN★★★★★

激活函数对比：ReLU、LeakyReLU、GELU、SiLU★★★★☆

优化技巧：梯度裁剪、学习率 warmup、Lookahead★★★☆☆

正则化方法：Dropout、Weight Decay、Label Smoothing★★★★☆

4. 工程与部署能力

Python 数据处理：Numpy/Pandas 熟练度★★★★★

PyTorch 基础：Dataset、Dataloader、Module、Optimizer★★★★★

模型保存与加载、Checkpoint 管理★★★★★

GPU 加速与显存优化（混合精度、梯度累积）★★★★☆

模型部署：ONNX、TensorRT、TorchScript★★★★☆

Linux/Git/Docker 基础★★★☆☆

1. 数学与概率统计

(1)线性代数：矩阵乘法、特征值/特征向量、SVD、PCA 原理★★★★★

矩阵乘法：

如图，矩阵A(m*n),B(n*o)相乘，可得到矩阵C(m*o),

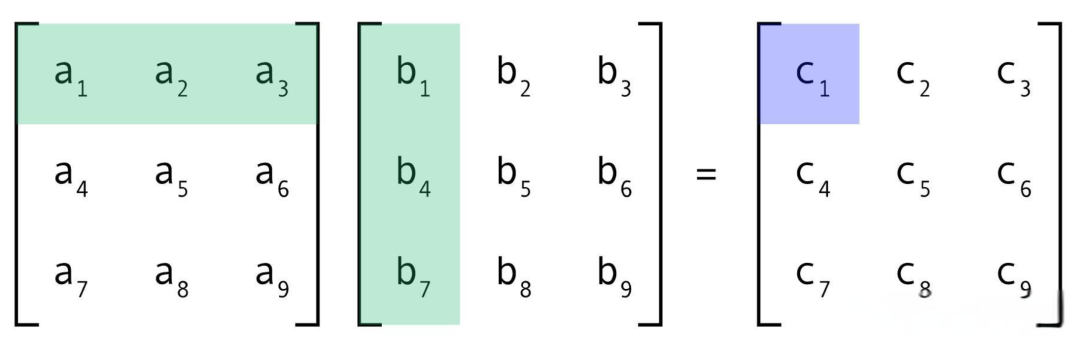
C矩阵中c1的计算：c_1 = a_1 b_1 + a_2 b_4 + a_3 b_7

普遍地，结果矩阵 C 第 i 行第 j 列元素 = 左矩阵A的第 i 行元素逐个乘右矩阵 B 第 j 列的元素的结果之和。

关于矩阵乘法的本质，可以理解为是一系列线性变换的复合，具体可参考此视频：

3Blue1Brown：线性代数的本质 - 04 - 矩阵乘法与线性变换复合

特征值/特征向量：

        数学上定义，当 Ax=\lambda x 时，x 是A的特征向量，\lambda 是A的特征值( \lambda是一常数)。

        我们来通俗地理解一下。由于上面我们说到了矩阵乘向量的本质是对向量进行线性变换，而几何上，线性变换可能对向量进行旋转、缩放、剪切等操作，那么有：

  • 特征向量：在变换中方向不变的向量（仅被拉伸或压缩）。
  • 特征值：对应的缩放因子

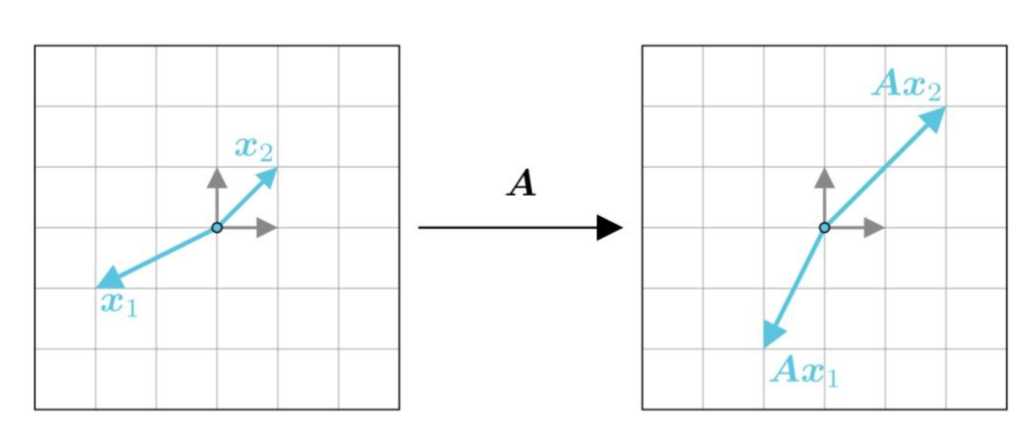
        举个例子，在上图中，向量x_2经过变换 A 之后方向不变，只是长度增加，故x_2是 A的特征向量，特征值则是2。

SVD 奇异值分解：

此处参考 知乎链接

奇异值分解是 LoRA微调的理论基础。正因为矩阵可以分解为D_{r \times r}，后续才可以用lora_A和lora_B两个参数量显著减小的矩阵，对网络参数进行更新，得到接近全量更新的结果。

PCA（priority component analysis）主成分分析：

        对高维数据进行降维

协方差与协方差矩阵：

111

PCA算法流程：

 参考链接 知乎 - 主成分分析

(2)概率论：条件概率、贝叶斯公式、联合分布、期望/方差★★★★★

条件概率：

贝叶斯公式：

联合分布：

期望：对数据取值和取值概率相乘并进行求和。

方差：可用来衡量数据分布散度。方差越小，数据分布越集中。

(3)最大似然估计与最大后验估计★★★★★

似然：

        我们常用概率(Probability) 来描述一个事件发生的可能性。

        而似然性(Likelihood) 正好反过来，意思是一个事件实际已经发生了，反推在什么参数条件下，这个事件发生的概率最大。

        用数学公式来表达上述意思，就是:

  • 已知参数 β 前提下，预测某事件 x 发生的条件概率为P(x|\beta)  ;
  • 已知某个已发生的事件 x，未知参数 β 的似然函数为L=(\beta | x)  ；
  • 上面两个值相等 ( 为什么？)，即：P(x|\beta) = L(\beta |x) 。

        一个参数 β 对应一个似然函数的值，当 β 发生变化，L=(\beta | x)也会随之变化。当我们在取得某个参数的时候，似然函数的值到达了最大值，说明在这个参数下最有可能发生x事件，即这个参数最合理。

最大似然估计（MLE）：求β在取什么值的时候，L(β)能达到最大值

参考链接： 知乎 - 用人话讲明白梯度下降

最大后验估计（MAP）：

参考链接： 知乎 - 究竟什么是最大后验估计

(4)信息论：熵、交叉熵、KL散度、互信息★★★★☆

(5)优化理论：梯度下降、牛顿法、动量法、Adam、学习率调度★★★★★

梯度下降：

牛顿法：

动量法：

Adam：

(6)凸优化与约束优化基础★★★☆☆

高数基础：偏导数链式法则、泰勒展开★★★☆☆

2. 机器学习基础

(1)经典算法：逻辑回归、SVM、KNN、朴素贝叶斯、决策树★★★★★

逻辑回归：

SVM（support Vector Machine）：试图找到使得各类样本点到超平面距离最远的，即最大间隔的超平面。

        首先，我们需要知道，在二维空间上，两类点被一条直线完全分开叫做线性可分（如图所示）。

严格的数学定义是：

        从二维扩展到多维空间中时， 将D_0 和 D_1 完全正确地划分开的 wx+b=0 (二维空间中区分开两种类型的点的那条直线) 就成了一个超平面。

        为了使这个超平面更具鲁棒性，我们会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面，具有以下性质：

  • 两类样本分别分割在该超平面的两侧；
  • 两侧距离超平面最近的样本点到超平面的距离被最大化了。

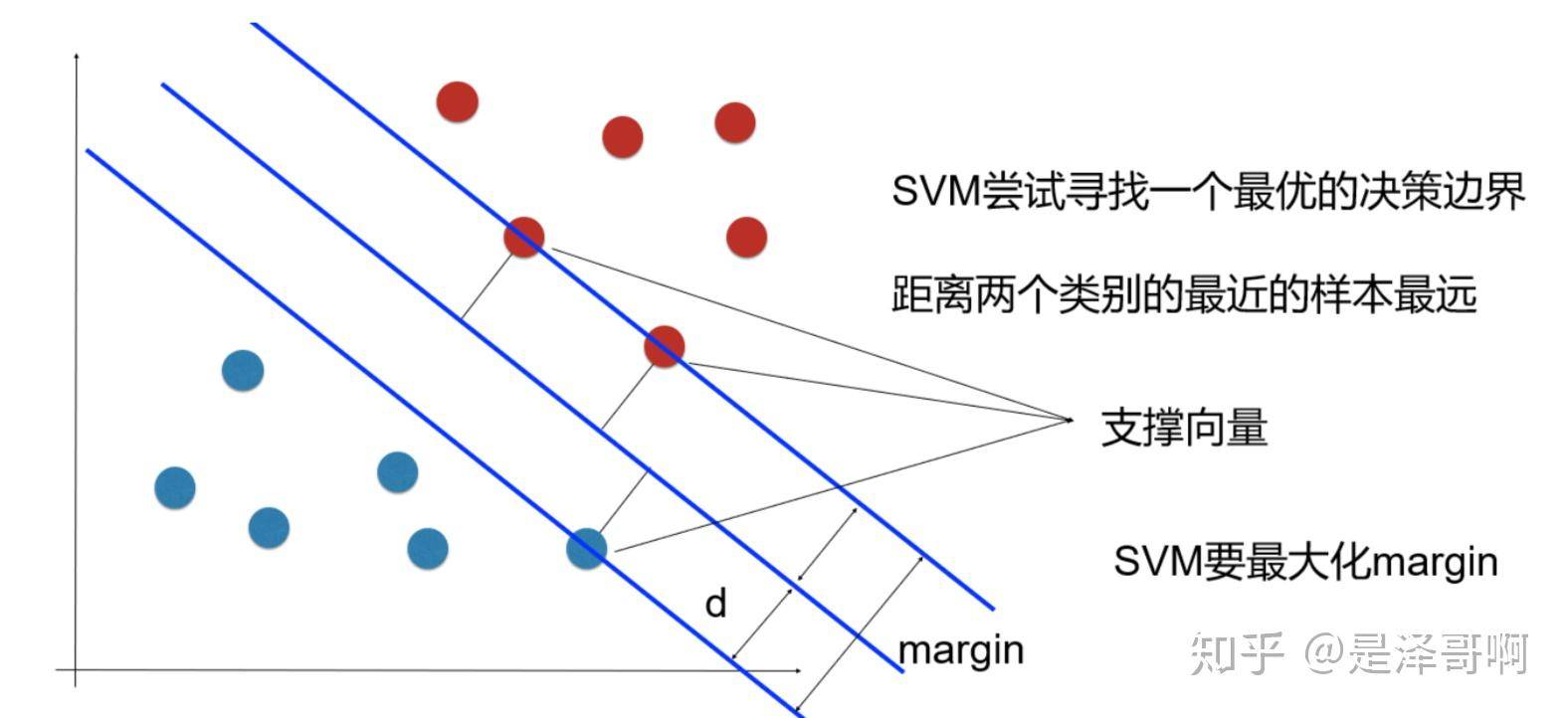
样本中距离超平面最近的一些点，叫做支持向量。

参考链接：知乎 - 支持向量机

KNN（K-nearest neighbours）：K最邻近算法，选取已知类别的数据中和当前数据 x 距离最近的 K个点，根据这K个点的类别，来判断点 x 所属的类别

集成方法：Random Forest、GBDT、XGBoost、LightGBM★★★★★

模型评估：ROC/AUC、Precision-Recall、F1-score、混淆矩阵★★★★★

Accuracy：

        表示模型预测正确的样本数占总样本数的比例。然而，在类别不平衡的数据集中，准确率可能会产生误导。例如，在一个90%样本属于A类，10%样本属于B类的二分类问题中，即使模型始终预测为A类，准确率也有90%，但模型对B类的识别能力为零。

        准确率是衡量分类模型性能的基础指标，它表示模型正确预测的样本数占总样本数的比例。在二分类问题中，准确率的计算公式为：

Accuracy = \frac{TP+TN}{TP+TN+FP+FN}

        其中，TP代表真正例，TN代表真负例，FP代表假正例，FN代表假负例。

Precision 精确率：衡量模型预测为正类的样本中，实际为正类的比例。

        精确率关注的是模型预测为正类别的样本中，真正为正类别的样本的比例。精确率的计算公式为：

Precision = \frac{TP}{TP+FP}

        精确率越高，说明模型对正类别的识别能力越强，即模型预测为正的样本中，实际为正的比例越高。在信息检索和推荐系统中，精确率是一个重要的指标，因为它直接关系到用户或系统对结果的满意度。精确率高意味着模型在预测正类时错误较少。在医疗诊断中，精确率高的模型可以减少误诊率。

Recall 召回率：

        衡量实际为正类的样本中，被模型正确预测为正类的比例。召回率高意味着模型能够识别大多数的正类样本。在疾病筛查中，高召回率可以确保尽可能多的患者被检测出来。

        召回率衡量的是所有实际为正样本的样本中，被模型正确预测为正样本的比例。召回率的计算公式为：

 Recall = \frac{TP}{TP+FN}

ROC/AUC：

参考链接：知乎 - 一文看懂深度学习模型评估

欠拟合与过拟合解决方案：正则化、数据增强、早停★★★★★

欠拟合：模型在当前数据集的拟合不佳，即通常所说的训练未收敛（？），可以理解为模型在当前数据集上的表现不好。

过拟合：模型被过度限制在当前数据集的特征空间，导致对训练集外的数据预测准确率下降，通常由训练轮数过大导致，表现为train loss下降或不变，val loss上升

特征工程：标准化/归一化、特征交互、降维（PCA、t-SNE）★★★★☆

超参数搜索：网格搜索、随机搜索、Bayesian Optimization  ★★★★☆

3. 深度学习核心

神经网络基本结构：前向传播/反向传播★★★★★

        优化神经网络参数的过程，实际上是找到最佳的网络参数 W ，使输入 X 经过网络的变换得到的 \hat{Y} 尽可能接近真实值 Y。

        那么，前向传播，即是根据网络中上一层结点，计算网络中当前层结点的激活值，直至网络最后一层，计算得到 \hat{Y}的过程。

        而反向传播，指的是如果当前代价函数（损失函数）值距离预期值较远，那么我们通过调整参数 W 和偏置 b 的值，使新的代价函数值更接近预期值（和预期值相差越大，则w和b调整的幅度就越大）。一直重复该过程，直到最终的代价函数值在误差范围内，则算法停止。

前向传播：

反向传播：

参考链接：CSDN - 前向传播与反向传播 

CNN：卷积/池化、padding、stride、感受野★★★★★

卷积：

池化：池化（pooling）的本质，其实就是采样。对于输入的特征图，选择某种方式对其进行降维压缩，以加快运算速度。这词其实是汇聚（到池子里）的意思，疑似当年第一个翻译成池化的人英语不太好。

        最大池化（MaxPooling）：选择filter内最大值输出到下一层

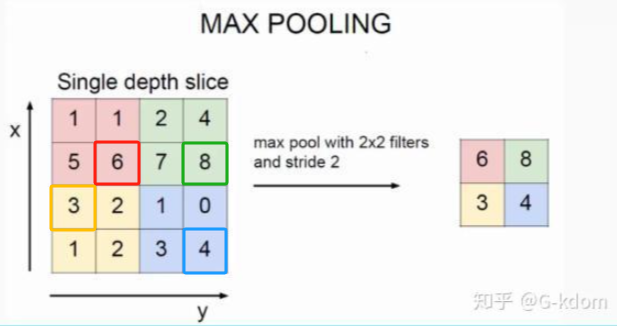
        如上图所示，表示的就是对一个 4×4 特征图邻域内的值，用一个 2×2 的filter，步长为2进行‘扫描’，选择最大值输出到下一层，这叫做 Max Pooling。

        max pooling常用的 s=2 ， f=2 的效果：特征图高度、宽度减半，通道数不变。

【池化层没有参数、池化层没有参数、池化层没有参数】 

池化的作用：

（1）保留主要特征的同时减少参数和计算量，防止过拟合。

（2）invariance(不变性)，这种不变性包括translation(平移)，rotation(旋转)，scale(尺度)。

        Pooling 层说到底还是一个特征选择，信息过滤的过程。也就是说我们损失了一部分信息，这是一个和计算性能的一个妥协。

参考链接：知乎 - 池化

padding（填充）：指的是在进行卷积操作时,对输入进行边缘填充,以控制输出特征图的大小和形状。

常见的padding方式有：

stride（步长）：滑动卷积核时，我们会先从输入的左上角开始，每次往右左滑动一列或者往下滑动一行逐一计算输出，我们将每次滑动的行数或列数称为Stride。

感受野：

        指卷积神经网络每一层输出的特征图(feature map)上每个像素点映射回输入图像上的区域大小。

        神经元感受野的范围越大表示其能接触到的原始图像范围就越大，也意味着它能学习更为全局，语义层次更高的特征信息；相反，范围越小则表示其所包含的特征越趋向局部和细节。因此感受野的范围可以用来大致判断每一层的抽象层次。并且我们可以很明显地知道网络越深，神经元的感受野越大。

        由此可知，深度卷积神经网络中靠前的层感受野较小，提取到的是图像的纹理、边缘等局部的、通用的特征；靠后的层由于感受野较大，提取到的是图像更深层次、更具象的特征。

        因此在迁移学习（模型微调）中常常会将靠前的层的参数冻结（不参与训练，因为他们在迁移到新的场景之前已经具备了提取通用特征的能力），来节省训练的时间和算力消耗。

参考链接：知乎 - CNN基础知识

RNN / LSTM / GRU：序列建模原理★★★★☆

 RNN：循环神经网络。 t 时的输出 由 t 时刻的输入 x_t 和 t-1 时的隐藏状态h_{t-1}决定

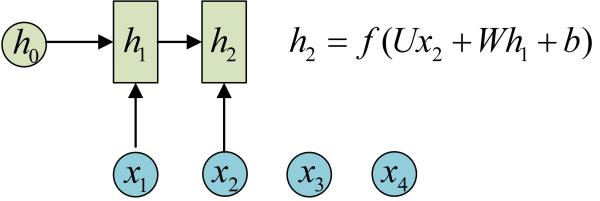
        为什么叫“循环”神经网络嘞？因为它还可以表示成这样：

        在这个结构中，每个神经网络的模块A，读取某个输入x_{t}和上一时间步的隐藏状态h_{t-1}，并输出一个值h_{t}。“循环”之处在于，每个h_{t}都经过 共享的 模块A，产生下一个隐藏状态，再次输入模块A 。

LSTM（Long-short term memory）：长短时记忆网络

        RNN 的结构如此清晰明了，看上去天然适用于序列类输入（例如文本或音频），然而实际上， 在递归神经网络中，获得小梯度更新的层会停止学习—— 那些通常是较早的层。

        由于这些层不学习，RNN会忘记它在较长序列中以前看到的内容，因此RNN只具有短时记忆，即对于时刻 t ，上一时间步的输入 x_{t-1} 对当前时刻的输入x_{t} 的影响显然会强于 x_{t-1000}。如果一条序列足够长，那它们将很难将信息从较早的时间步传送到后面的时间步。

        而LSTM——一种RNN特殊的类型，可以学习长期依赖信息。LSTM和基线RNN并没有特别大的结构不同，但是它们用了不同的函数来计算隐状态。

        LSTM的“记忆”我们叫做细胞/cells，它的输入为前状态和h_{t-1}当前输入x_t。这些“细胞”会决定哪些之前的信息和状态需要保留/记住，而哪些要被抹去。实际的应用中发现，这种方式可以有效地保存很长时间之前的关联信息。

        LSTM有通过精心设计的称作为“门”的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个sigmoid神经网络层和一个pointwise乘法的非线性操作。

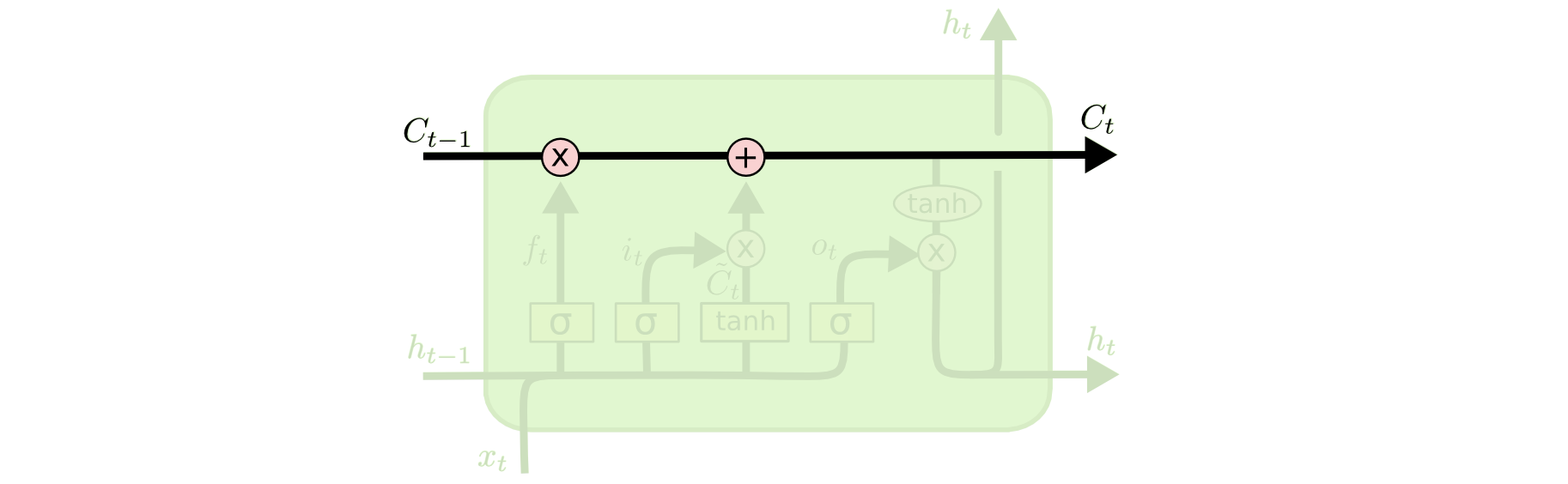
        LSTM内部包括三种类型的门结构：遗忘门/忘记门、输入门和输出门，来保护和控制细胞状态。

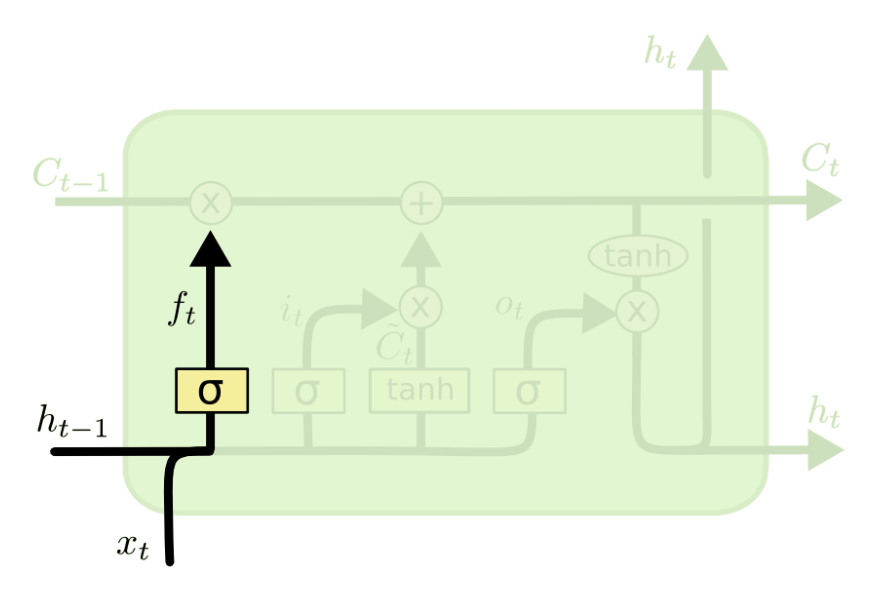遗忘门：选择性遗忘之前的内容‘

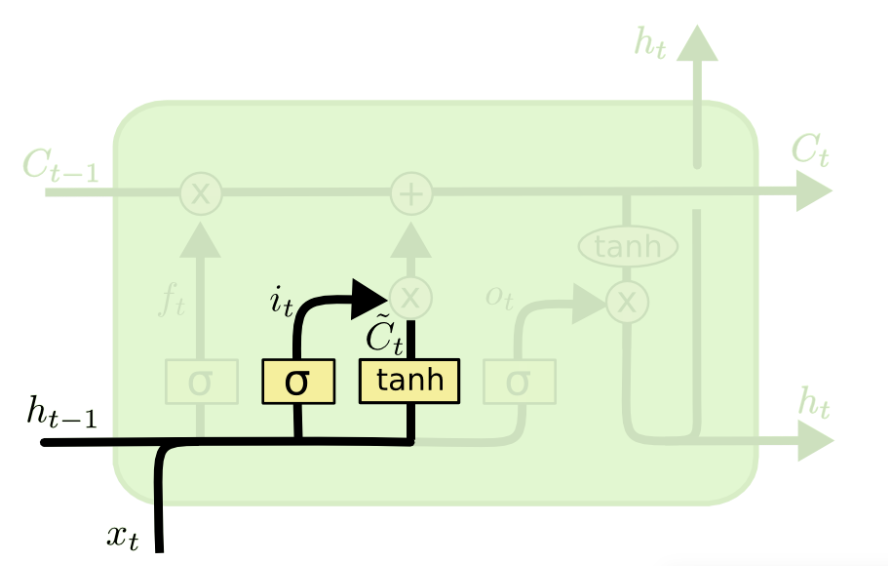记忆门：决定保留哪些内容

这里包含两个部分：

  1. 第一，sigmoid层称“输入门层”决定我们要更新什么值；
  2. 第二，一个tanh层创建一个新的候选值向量\tilde{C}_{t}，会被加入到状态中

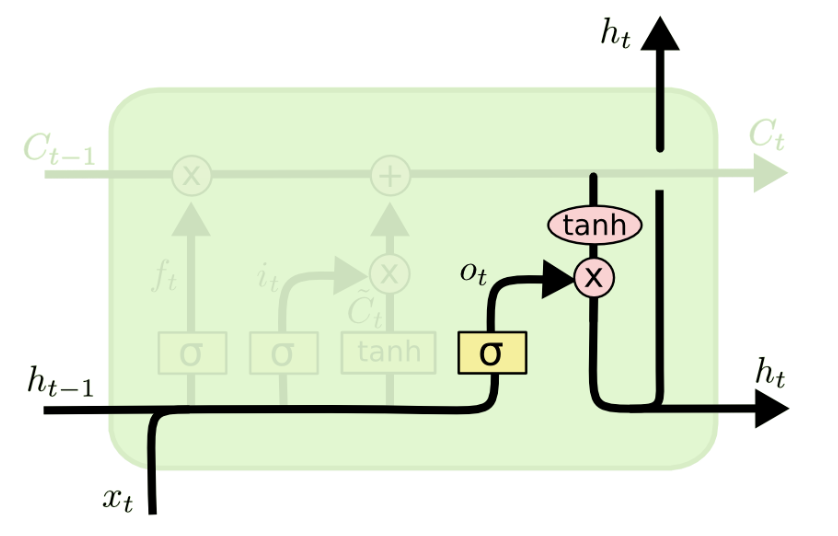其中i_{t} = \sigma (W_{ih}h_{t-1} + W_{ix}x_{t} + b_{i})，\tilde{C_{t}} = tanh(W_{Ch}h_{t-1} + W_{Cx}x_{t} + b_{C})

输出门：在当前时间步细胞状态 C_{t}的参与下（注意！这里不是上一时间步的细胞状态，因为其已经和通过遗忘门、记忆门的运算结果进行了运算），根据前一时间步隐藏状态h_{t-1}和当前时间步输入x_t得到新的隐藏状态。

        你可以理解为循环神经网络的输出本质上是时刻 t 的隐藏状态。

        更新细胞状态（仅用到遗忘门和输入门，放在这里是为了将三个门先介绍清楚）：

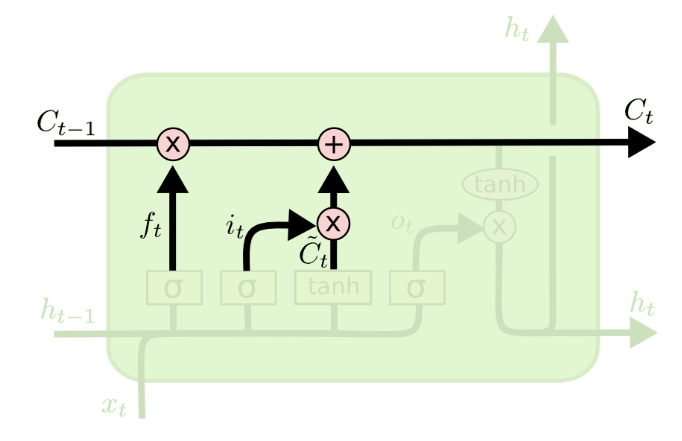 细胞状态与遗忘门的输出相乘，决定忘记哪些内容；

  然后与输入门的输入相加，决定记住哪些新内容。

GRU (Gated Recurrent Unit) 门控循环单元：

        将LSTM的忘记门和输入门合成了一个单一的更新门，同时还混合了细胞状态和隐藏状态。

为了便于理解，把上图右侧中的前三个公式展开一下

r_{t} = \sigma (W_{rh}h_{t-1} + W_{rx}x_{t})

\tilde{h} = tanh(W_{rh}(r_{t}h_{t-1}) + W_{x}x_{t})
        这里面有个小问题，r_t 和 z_t 都是对h_{t-1} 、x_t做的Sigmoid非线性映射，那区别在哪呢？原因在于GRU把忘记门和输入门合二为一了，而 z_t 是属于要记住的，反过来 1-z_t 则是属于忘记的，相当于对输入h_{t-1} 、x_t做了一些更改/变化，而 r_t 则相当于先见之明的把输入、在 z_t / 1-z_t 对其做更改/变化之前，先事先存一份原始的，最终在 h_t 那做一个tanh变化。

参考链接：CSDN - 长短时记忆网络

Transformer 架构：多头注意力、位置编码、残差连接★★★★★

残差网络、DenseNet 与梯度流问题★★★★★

归一化技术：BN vs LN vs GN★★★★★

激活函数对比：ReLU、LeakyReLU、GELU、SiLU★★★★☆

优化技巧：梯度裁剪、学习率 warmup、Lookahead★★★☆☆

正则化方法：Dropout、Weight Decay、Label Smoothing★★★★☆

1

4. 工程与部署能力

  • Python 数据处理：Numpy/Pandas 熟练度★★★★★

  • PyTorch 基础：Dataset、Dataloader、Module、Optimizer★★★★★

  • 模型保存与加载、Checkpoint 管理★★★★★

  • GPU 加速与显存优化（混合精度、梯度累积）★★★★☆

  • 模型部署：ONNX、TensorRT、TorchScript★★★★☆

  • Linux/Git/Docker 基础★★★☆☆

网站公告

今日签到

点亮在社区的每一天
去签到

热门文章

最新发布